Группировка рабочих листов

Рассмотрим задачу решения СЛАУ на следующем примере

 

(7)

 

Т.е. будем решать систему из трех алгебраических уравнений относительно трех неизвестных. Размерность системы (7) n =3, матрица системы A (3) размерности 3´3 имеет вид

 

(8)

 

а вектор-столбец свободных членов (5) B =(-24, -48, 18) ^T.

Попытаемся решить СЛАУ (7) в среде MS Excel тремя различными способами. Для чего создадим рабочую книгу из трех листов и назовем ее Решение СЛАУ.xls. Поскольку исходные данные для трех различных способов решения (а значит и трех рабочих листов книги) одни и те же (матрица системы A (8) и вектор-столбец свободных членов B), то неплохо было бы их одновременно ввести в эти рабочие листы. Excel предоставляет такую возможность. Этот инструмент называется группировкой рабочих листов [4]. Для того, чтобы применить средство Группа, необходимо выделить группируемые рабочие листы, щелкнув первый рабочий лист (Лист1), на котором будут вводиться данные, а затем, удерживая клавишу Ctrl, щелкнуть ярлычки листов (Лист2 и Лист3), куда одновременно должны вводиться те же самые данные. Либо, если группируемые рабочие листы расположены подряд, как в нашем случае, при выделенном первом (Лист1) щелкнуть, удерживая нажатой клавишу Shift, на ярлычке последнего (Лист3). После этого можно вводить данные на текущем рабочем листе, они автоматически появятся в одноименных ячейках на всех остальных сгруппированных листах. Признаком группировки нескольких листов является появившееся в строке заголовка слово [Группа] ([Group]), заключенное в квадратные скобки (рис. 1). После ввода группировку необходимо отменить. Для отмены необходимо выбрать любой из листов, не входящих в группу, либо щелкнуть правой кнопкой мыши на любом ярлычке листа из группы и выполнить команду Разгруппировать листы.

Для решения рассматриваемой СЛАУ (7) сгруппируем листы (Лист1:Лист3), разместим в ячейках текущего листа (Лист1) A1, B2, D2, A6:A9 соответствующие поясняющие тексты (заголовки), в интервале A3:C5 – элементы матрицы A (8), а в интервале D3:D5 – элементы вектора B. Интервал B7:B9 зарезервируем под искомое решение – вектор X (4). После этих манипуляций все три рабочих листа примут одинаковый вид (рис. 1). Перед дальнейшей работой не забудьте разгруппировать рабочие листы.

 

Метод Крамера

 

Метод Крамера большинству известен еще со школьной скамьи. Решение СЛАУ (6) находится по формулам Крамера

 

(9)

 

где det A = ï A ï– определитель матрицы (3) системы (главный определитель),
det A_i = ï A_i ï (i = 1, 2, …, n)– определители матриц A_i (вспомогательные определители), которые получаются из A заменой i -го столбца на столбец свободных членов B (5). Линейная алгебраическая система несовместна (не имеет решений), если det A =0. Для рассматриваемой СЛАУ (7) вспомогательные матрицы имеют следующий вид

 

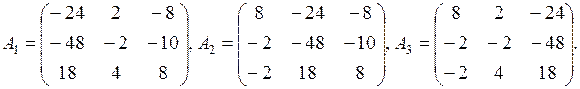
(10)

 

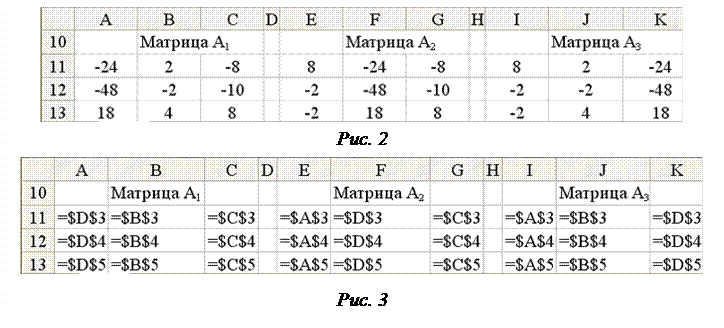
Разместим их на рабочем листе (рис. 2). Причем сделаем это не путем простого копирования соответствующих значений, а вводом формул с использованием абсолютных ссылок (рис. 3) на элементы матрицы A из интервала A3:C5 и элементы вектора B из интервала D3:D5 (рис. 1). Во-первых, это ускорит процесс ввода матриц A_i (i = 1, 2, 3) (формулы введем только в интервал A11:C13 матрицы A ₁ и в интервал E11:E13 первого столбца матрицы A ₂, далее же будем их блоками только копировать: A11:A13 в F11:F13 и в K11:K13, B11:B13 в J11:J13, C11:C13 в G11:G13, E11:E13 в I11:I13). Во-вторых, это сделает проектируемую таблицу универсальной в том смысле, что можно будет изменять только исходные данные (матрицу системы A в интервале A3:C5 и вектор-столбец свободных членов B в D3:D5), а все остальное (в том числе и решение СЛАУ) будет автоматически вычисляться.

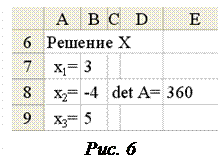
Далее, воспользовавшись функцией МОПРЕД(матрица), вычислим определители всех матриц (рис. 4). Аналогичная формула (=МОПРЕД(A3:C5)) для вычисления определителя матрицы A записана в ячейку E8. Осталось по формулам Крамера (9) найти решение системы (7). Соответствующие формулы Excel запишем в интервал решения B7:B9 (рис. 5), в котором и увидим результат (рис. 6). Обратите внимание на то (рис. 5), что при вычислении x_i (i = 1, 2, 3) анализируется значение определителя матрицы системы A, вычисленное в ячейке E8, и, если оно равно нулю (система несовместна), то в B7 помещается текст «Решения нет», а в ячейки B8 и B9 – пустые строки.

 

Матричный способ решения

 

Матричный способ решения СЛАУ (6) достаточно прост. Обе части матричного равенства (2) умножим слева на обратную матрицу А ^-1. Получим A ^-1´ A ´ X = A ^-1´ B. Т.к. A ^-1´ A = E, где E – единичная матрица (диагональная матрица, у которой по главной диагонали расположены единицы). Тогда решение системы (2) запишется в следующем виде

 

X = A -1 ´ B.

(11)

 

Т.е. для решения системы (2) (вычисления вектора-столбца X (4)) необходимо найти для матрицы A (3) обратную A ^-1 и умножить ее справа на вектор-столбец B (5) свободных членов. Для чего, воспользовавшись функциями Excel МУМНОЖ(матрица1;матрица2) и МОБР(матрица), введем в интервал B7:B9 следующего рабочего листа (Лист2) табличную, т.е. используя для ввода комбинацию Ctrl+Shift+Enter, мегаформулу =МУМНОЖ(МОБР(A3:C5);D3:D5). После чего в строке формул увидим {=МУМНОЖ(МОБР(A3:C5);D3:D5)}, а в интервале B7:B9 – решение, точно такое же, как и в предыдущем случае (рис. 6).

 

Поиск решения

 

Широкий класс экономических задач составляют задачи оптимизации. Задачи оптимизации предполагают поиск значений аргументов, доставляющих функции, которую называют целевой, минимальное или максимальное значение при наличии каких-либо дополнительных ограничений. MS Excel располагает мощным средством для решения оптимизационных задач. Это инструмент-надстройка, который называется Поиск решения (Solver) [5]. Поиск решения доступен через меню Сервис/Поиск решения.

Задачу решения СЛАУ (1) можно свести к оптимизационной задаче. Для чего одно из уравнений (например, первое) взять в качестве целевой функции, а оставшиеся n -1 рассматривать в качестве ограничений. Запишем систему (1) в виде

 

(12)

 

Тогда задача оптимизации для Поиска решения может звучать следующим образом. Найти значения X = (x₁, x₂, …, x_n) ^T, доставляющие нуль функции, стоящей слева в первом уравнении системы (12), при n -1 ограничениях, представленных оставшимися уравнениями.

Для решения этой задачи необходимо записать выражения (формулы) для вычисления значений функций, стоящих слева в уравнениях системы (12). Отведем под эти формулы интервал C7:C9 текущего рабочего листа (Лист3). В ячейку C7 введем формулу =A3*$B$7+B3*$B$8+C3*$B$9-D3 и скопируем ее в оставшиеся C8 и C9. В них появятся соответственно =A4*$B$7+B4*$B$8+C4*$B$9-D4 и =A5*$B$7+B5*$B$8+C5*$B$9-D5. Осталось, обратившись к пункту меню Сервис/Поиск решения, в окне диалога (рис. 7) задать параметры поиска (установить целевую ячейку C7 равной нулю, решение в изменяемых ячейках B7:B9, ограничения заданы формулами в ячейках C8 и С9). После щелчка по кнопке Выполнить в интервале B7:B9 получим результат (рис. 8) – решение СЛАУ (7).

В завершение работы можно защитить ячейки созданных таблиц от несанкционированного, часто случайного, изменения и скрыть формулы, по которым находится решение СЛАУ. Для этого существует стандартное средство Excel – пункт меню Сервис/Защита/Защитить лист. Перед этим необходимо снять защиту с ячеек, содержащих исходные данные (A3:C5 – элементы матрицы A (8), и D3:D5 – элементы вектора B), выделив эти интервалы, выбрав меню Формат/Ячейки вкладка Защита и сбросив флажок Защищаемая ячейка. Для ячеек же, содержащих формулы, надо в этом диалоге (Формат ячеек) установить флажок Скрыть формулы. Надо знать, что после такой защиты невозможно будет воспользоваться средством Поиск решения. Поэтому защитить ячейки и скрыть формулы можно на первом и втором листах. В случае необходимости можно скрыть и отображаемую в ячейках информацию, поставив в соответствие этим ячейкам пользовательский формат;;; (три точки с запятой).

 

ЗАДАНИЕ ДЛЯ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

 

В соответствии с номером варианта выберите из приведенных ниже систему линейных алгебраических уравнений четвертого (n =4) порядка. Приведите ее к нормальному виду (1). Разработайте таблицы Excel для решения выбранной СЛАУ тремя различными способами:

1) методом Крамера (п. 2.3),

2) матричным способом (п. 2.4),

3) используя Поиск решения (п. 2.5).

Варианты систем линейных алгебраических уравнений:

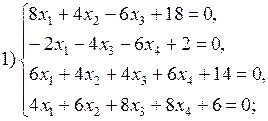
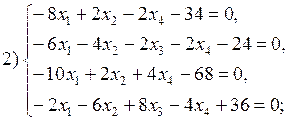
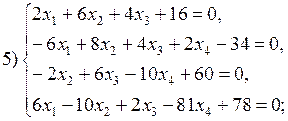
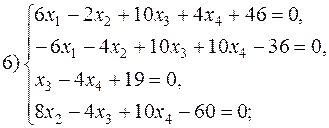
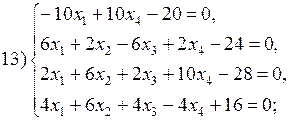
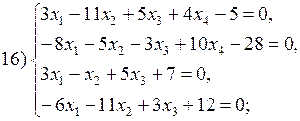
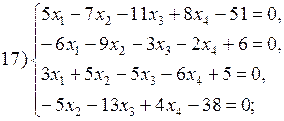
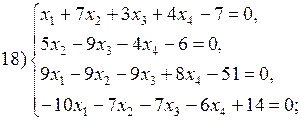
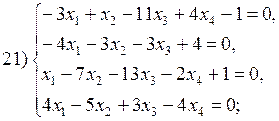
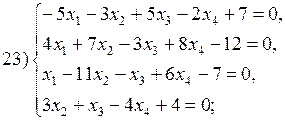
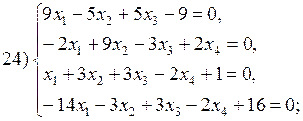
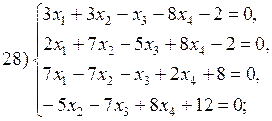
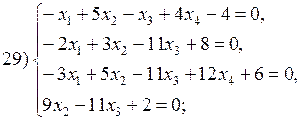
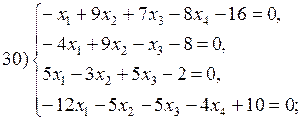
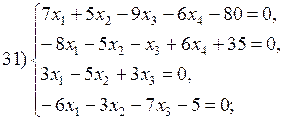
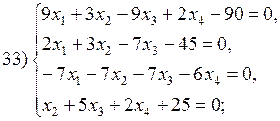
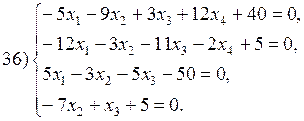
Правильность полученных решений легко проверить. В результате решения выбранной СЛАУ тремя различными способами должны получиться три одинаковых решения. Однако, на всякий случай, приведем решения систем 1)-36):

1)-6) X = (-5,1,-3,4) T;	7)-12) X = (1,-3,-1,0) T;	13)-18) X = (1,0,-2,3) T;
19)-24) X = (1,0,0,1) T;	25)-30) X = (0,1,1,0) T;	30)-36) X = (5,0,-5,0) T.

 

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

 

1. Вержбицкий В.М. Основы численных методов: Учебник для вузов.- 2-е изд., перераб.- М.: Высшая школа, 2005.- 840 с.

2. Лавренов С.М. Excel: Сборник примеров и задач.- М.: Финансы и статистика, 2002.- 336 с.

3. Гельман В.Я. Решение математических задач средствами Excel: Практикум.- СПб.: Питер, 2003.- 237 с.

4. Холи Р. Excel. Трюки/ Р. Холи, Д. Холи.- СПб.: Питер, 2005.- 287 с.

5. Решение уравнений средствами Excel: Методические указания к лабораторным работам/ Сост.: Е.Е. Дадонова, А.Г. Пимонов, М.А. Тынкевич; ГУ Кузбас. гос. техн. ун-т.- Кемерово, 2002.- 22 с.

Составители