Определение объема тела
Цель работы.
Научиться рассчитывать погрешности измерения физической величины.
Теоретические сведения.
Объем тела V, имеющего форму параллелепипеда, рассчитывается по соотношению:
V = a×b×c, (1)
где a, b, c - линейные размеры тела (см. рис. 1).
Рис. 1.
Случайная погрешность прямого измерения величины X, полученной в серии из n измерений, рассчитывается по формуле:
, (2)
где t(p,n)- коэффициент Стьюдента (для доверительной вероятности p= 0,95);
- среднеквадратичная погрешность величины Х, полученная в серии из n измерений;
Xi - измеренное значение физической величины;
n - число измерений в серии;
- среднее значение измеряемой величины;
Расчет случайной погрешности измерения объема («методом дифференцирования»):
Объем параллелепипеда получен в результате косвенного измерения. Среднеквадратичная погрешность косвенного измерения величины объема sV рассчитывается по формуле («метод дифференцирования»):
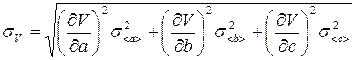, (3)
где 
, 
, 
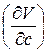- частные производные объема по переменным a, b, c;
s< a >, s< b >, s< c > - среднеквадратичные погрешности измерения величин a, b и c.
Продифференцируем выражение (1) и подставим в (3). Получим:
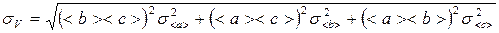, (4)
где < a >, < b > и <c > - средние значения величин a, b и c.
Упростим формулу (4). Поделим левую и правую часть равенства на величину
<V> = < a >< b > <c > и умножим на коэффициент Стьюдента t(p,n).
Получим простую и удобную формулу для расчета случайной погрешности измерения объема («методом дифференцирования»):
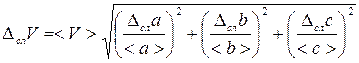, (5)
где D слa, D слb, D сл c - случайные погрешности прямого измерения величин a, b и с;
< a >, < b > и <c > - средние значения величин a, b и c.
Для расчета суммарной погрешности измерения объемаследует воспользоваться формулой:
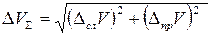, (6)
где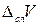 
- случайная погрешность измерения объема;
- приборная погрешность измерения объема.
Методика проведения измерений.
1. Измеряем миллиметровой линейкой линейные размеры параллелепипеда a, b и c не менее пяти раз, результаты заносим в таблицу.
2. Рассчитываем средние значения измеренных величин < a >, < b > и <c >.
3. Результаты заносим в соответствующие клеточки таблицы.
4. Рассчитываем случайные погрешности прямых измерений D слa, D слb, D сл c по формуле (2). Результаты запишем в таблицу.
5. Запишем приборные погрешности измерений Dпр a, Dпр b, Dпрc в соответствующую строку таблицы (приборная погрешность прямого измерения линейных размеров тела измерительной линейкой, в основном, определяется погрешностью отсчета, т. е. равна половине цены деления измерительной линейки: Dпр a = Dпр b = Dпр c = 0,5 мм).
6. Рассчитаем пять значений объема, запишем результаты в таблицу (по первому набору параметров a, b, c рассчитать по формуле (1) первое значение объема V1, по второму набору значений a, b, c рассчитать второе значение объема V2. Таким же образом рассчитать объем для всех наборов параметров a, b, c. В результате мы получим набор значений объема: V1, V2… Vn).
7. Рассчитаем <V>.
8. Рассчитаем 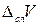двумя способами, (для расчета приборной погрешности измерения объемаследует воспользоваться полученной нами формулой (5), где вместо D слa, D слb, D сл c будут стоять приборные погрешности измерения величин Dпр a, Dпр b, Dпрc).
9. Рассчитаем 
(Для расчета суммарной погрешности измерения объемаследует воспользоваться формулой (6)). Результаты занесем в таблицу.
10. Рассчитаем относительную погрешность измерения объема d V по формуле: 
×100%
11. Результат запишем в таблицу.
12. Записываем результат измерения объема в стандартном виде с указанием абсолютной и относительной погрешности (доверительные интервалы).
| № | а, мм | b, мм | c, мм | V, мм3 метод Стьюдента | V, мм3 метод дифференцирования |
| <X> | |||||
| s<X>, | |||||
| |||||
| |||||
| |||||
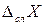
| d Х |
