«Методы изучения корреляционных связей.»
1. Наиболее простым методом определения степени связи между признаками является:
1) метод Спирмена
2) метод контингенции Пирсона
3) метод стандартизации 1.
2. Наиболее точным методом определения степени связи между качественными признаками является:
1) метод парной корреляции
2) метод ранговой корреляции
3) j2 (фи-квадрат)
3. Корреляционная связь может быть прямой и
1) обратной
2) косвенной
4. Коэффициент корреляции, равный нулю, свидетельствует:
1) об отсутствии связи между явлениями
2) о слабой связи между явлениями
3) о слабой отрицательной связи между явлениями
5. Коэффициент корреляции, равный единице, свидетельствует:
1) о наличии функциональной связи между явлениями
2) о наличии сильной корреляционной связи между явлениями
6. Коэффициент ранговой корреляции рассчитывается при числе коррелируемых пар:
1) не менее 5
2) не менее 30
3) не менее 10
7. Связь между признаками считается статистически значимой, если величина коэффициента корреляции больше или равна табличной при:
1) Р=0,05
2) Р=0,5
3) Р=0,2
8. Связь между признаками считается статистически значимой, если коэффициент корреляции превышает свою ошибку:
1) в 3 и более раз
2) в 2 и более раза
3) в 1,5 и более раза
9. Коэффициент корреляции, равный «-0,3», свидетельствует:
1) о слабой отрицательной связи между явлениями
2) о средней отрицательной связи между явлениями
3) об отсутствии связи между явлениями
10. Корреляционная связь характеризуется соответствием:
1) нескольких значений одного признака одному значению второго признака;
2) одного значения первого признака строго определенному значению второго признака.
11. Практическое использование корреляционного анализа:
1) расчет обобщающих коэффициентов, характеризующих различные стороны каждого из изучаемых признаков;
2) сравнение степени однородности исследуемых совокупностей;
3) определение пределов возможных колебаний совокупностей;
4) выявление взаимодействия факторов, определение силы и направления влияния одних факторов на другие.
12. Корреляционный анализ используется для:
1) расчета обобщающих коэффициентов, характеризующих различные стороны каждого из изучаемых признаков;
2) сравнения степени однородности исследуемых совокупностей;
3) определение пределов возможных колебаний выборочных показателей при данном числе наблюдений;
4) выявления взаимодействия факторов, определение силы и направленности.
13. Корреляционной называется связь:
1) дающая полную характеристику совокупности по ее гомогенности, особенности распределения двух сравниваемых признаков;
2) при которой значению каждой величины одного признака соответствует несколько значений другого взаимосвязанного с ним признака;
3) при которой любому значению одного из признаков соответствует строго определенное значение другого взаимосвязанного с ним признака.
14. Функциональной называется связь:
1) при которой значению каждой величины одного признака соответствует несколько значений другого взаимосвязанного с ним признака;
2) дающая полную характеристику совокупности по ее гомогенности, особенности распределения двух сравниваемых признаков;
3) при которой любому значению одного из признаков соответствует строго определенное значение другого взаимосвязанного с ним признака.
15. Корреляционная связь определяется, как связь:
1) при которой любому значению одного из признаков соответствует строго определенное значение другого взаимосвязанного с ним признака;
2) при которой значению каждой величины одного признака соответствует несколько значений другого взаимосвязанного с ним признака;
3) дающая полную характеристику совокупности по ее гомогенности, особенности распределения двух сравниваемых признаков.
16. Расчет коэффициента ранговой корреляции используется для:
1) определения взаимосвязи между двумя меняющимися признаками;
2) установление связи между несколькими статистическими совокупностями;
3) для характеристики корреляций в случаях нелинейной связи и для данных, распределение которых отличается от нормального;
4) оценки достоверности различия двух величин.
17. Условия для расчета коэффициента ранговой корреляции:
1) для расчета используются негруппированные ряды значений двух признаков;
2) достаточно ориентировочных данных об уровне признака;
3) расчет изменения величины одного признака при изменении величины другого признака на единицу;
4) расчет производится только между количественными признаками.
18. Укажите правильную формулу для расчета коэффициента ранговой корреляции:
1) 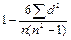
2) 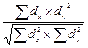
3) 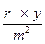
4) 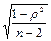
19. Расчет  используется для:
используется для:
1) определения достоверности различия нескольких совокупностей по распределению в них какого-либо признака;
2) оценки достоверности различия двух средних величин;
3) определения взаимосвязи между двумя количественными признаками, один из которых представлен в виде интервалов значений;
4) определения взаимосвязи между двумя меняющимися количественными признаками.
20. Укажите правильную формулу для расчета коэффициента линейной корреляции (Пирсона):
1) 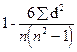
2) 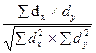
3) 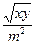
21. Значения коэффициента корреляции, превышающее табличное при Р = 95%, подтверждает статистическую:
1) достоверность;
2) недостоверность результатов.
22. Значение  , превышающее табличное при Р = 95%, подтверждает статистическую:
, превышающее табличное при Р = 95%, подтверждает статистическую:
1) достоверность;
2) недостоверность результатов.
УСТАНОВИТЕ СООТВЕТСТВИЕ
| 23. Корреляционная связь: | Значение | 
|
| 1) прямая сильная; 2) прямая слабая; 3) обратная слабая; 4) обратная средней силы. Одной цифре соответствует только одна буква. | А. Б. В. Г. Д. Е. Ж. З. | 0,2 0,9 -0,4 -0,12 1,5 -1,1 -2,4 1,1 |
| 24. Корреляционная связь: | Значение | 
|
| 1) прямая слабая; 2) обратная средней силы; 3) прямая сильная; 4) обратная сильная. Одной цифре соответствует только одна буква. | А. Б. В. Г. Д. Е. Ж. З. | 0,95 -0,2 -0,5 -0,9 0,24 -1,0 -1,1 -2,8 |
| 25. Корреляционная связь: | Значение | 
|
| 1) прямая слабая; 2) обратная средней силы; 3) прямая сильная; 4) обратная слабая. Одной цифре соответствует только одна буква. | А. Б. В. Г. Д. Е. Ж. З. | -0,5 1,4 0,1 -0,2 -1,4 0,9 2,0 -0,95 |
| 26. Корреляционная связь: | Значение | 
|
| 1) обратная слабая; 2) прямая сильная; 3) обратная средней силы; 4) прямая слабая. Одной цифре соответствует только одна буква. | А. Б. В. Г. Д. Е. Ж. З. | 0,39 0,11 0,9 1,3 -0,27 -0,56 0,9 -1,42 |
| 27. Корреляционная связь: | Значение | 
|
| 1) прямая сильная; 2) обратная средней силы. 3) прямая слабая; 4) обратная слабая; Одной цифре соответствует только одна буква. | А. Б. В. Г. Д. Е. Ж. З. | 1,0 -0,2 0,6 -0,65 0,25 0,9 -0,8 2,5 |
ОТВЕТЫ К ТЕСТОВЫМ ВОПРОСАМ
«Относительные величины. Медико-демографические показатели.»
| Номер вопроса | Ответ | Номер вопроса | Ответ | Номер вопроса | Ответ |
| 1,3,4 | |||||
| 3,4 | |||||
«Оценка общественного здоровья: заболеваемость, инвалидность, физическое развитие»
| Номер вопроса | Ответ | Номер вопроса | Ответ | Номер вопроса | Ответ |
| 1,2,3,4 | |||||
| 1,2,3,4,6 | |||||
| 1-Г,2-Д,3-А | |||||
| 1-Б,2-Д,3-АВ | |||||
| 1-В,2-Г | |||||
«Использование метода стандартизации при оценке здоровья населения и показателей работы учреждений здравоохранения.»
| Номер вопроса | Ответ | Номер вопроса | Ответ | Номер вопроса | Ответ |
| 1,2,3 | |||||
| 1,3 |
«Динамические ряды»
| Номер вопроса | Ответ | Номер вопроса | Ответ | Номер вопроса | Ответ |
| 1-Б,2-А,3-Г,4-В | |||||
| 1-В,2-Б,3-Г,4-Д | |||||
| 1,2,3 | 1-В,2-Б,3-Г,4-Е | ||||
| 1-Д,2-Е,3-Б | 1-Г,2-В | ||||
| 1-А,2-В,3-Е,4-Б | 1-В,2-Г | ||||
| 1-Г,2-Б,3-В,4-А | 1-Б,2-А,3-АД | ||||
| 1-Д,2-В,3-А,4-Б |
«Средние величины, оценка разнообразия признака в вариационном ряду.
Оценка достоверности»
| Номер вопроса | Ответ | Номер вопроса | Ответ | Номер вопроса | Ответ |
| 1-Б,2-А,3-Г | |||||
| 1-Б,2-А,3-Д | |||||
| 1-В,2-А,3-Б | |||||
«Методы изучения корреляционных связей.»
| Номер вопроса | Ответ | Номер вопроса | Ответ | Номер вопроса | Ответ |
| 1-Б,2-А,3-Г,4-В | |||||
| 1-Д,2-В,3-А,4-Г | |||||
| 1-В,2-А,3-Е,4-Г | |||||
| 1-Д,2-В,3-Е,4-Б | |||||
| 1-Е,2-Г,3-Д,4-Б |






