Основные термины и определения. Методические указания по выполнению контрольной работы

Методические указания по выполнению контрольной работы

Требования к выполнению контрольной работы

Контрольная работа оформляется на листах формата А4 и содержит:

• титульный лист (форма приведена в приложении № 1);

• основную часть (решение задач);

• список использованной литературы.

Оформление решения каждой задачи должно включать в себя: условие задачи, решение с необходимыми пояснениями и комментариями, ответ.

Контрольная работа должна быть написана и сдана в сроки, установленные приказом начальника Санкт-Петербургского им. В.Б. Бобкова филиала РТА. Слушатель, не сдавший контрольную работу в срок, считается имеющим академическую задолженность и не допускается к сдаче зачета.

Задания и последовательность выполнения контрольной работы

ВЫЧИСЛЕНИЕ ИНДИВИДУАЛЬНОГО НОМЕРА КОНТРОЛЬНОЙ РАБОТЫ:

Номер варианта контрольной работы рассчитывается слушателем самостоятельно. Он равен остатку от деления числа, составленного из двух последних цифр номера зачетной книжки, на количество вариантов, и увеличенного на единицу.

Пример 1:

Номер зачетной книжки – 1051 73.

Количество вариантов работ – 10.

Остаток от деления 73 на 10 равен 3 (73/10=7 и 3 в остатке).

Номер варианта контрольной работы (3+1)= 4.

Значит, слушатель должен выполнить контрольную работу "Вариант 4".

Пример 2:

Номер зачетной книжки – 1051 07;

Количество вариантов работ – 10;

Остаток от деления 07 на 10 равен 7 (07/10=0 и 7 в остатке);

Номер варианта контрольной работы (7+1)= 8.

Значит, слушатель должен выполнить контрольную работу "Вариант 8".

ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ ДЛЯ СЛУШАТЕЛЕЙ ЗАЧНОГО ОТДЕЛЕНИЯ

КОНТРОЛЬНАЯ РАБОТА №1

Вариант № 1

Задание № 1

по теме "Дифференциальное исчисление функции одной переменной"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

y = a = 2; а = 3; а ® ¥.

2. Вычислить производную функций.

1).

2).

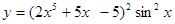
3. Вычислить y' в точке x₀.

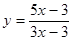; x₀= 5.

4. Найти экстремумы функции.

5. Найти наибольшее и наименьшее значение функции y на отрезке [0, 7]:

6. Вычислить .

; a = 1.

Задание № 2

по теме "Интегральное исчисление функции одной переменной"

1. Вычислить неопределенный интеграл

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл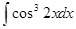

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл

7. Решить дифференциальное уравнение

8. Решить задачу Коши

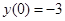
Вариант № 2

Задание № 1

по теме "Дифференциальное исчисление функции одной переменной"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

a = 0; а = 2; а ® ¥.

2. Вычислить производную функций.

1).

2).

3. Вычислить y' в точке x₀.

; x₀= – 5.

4. Найти экстремумы функции.

5. Найти наибольшее и наименьшее значение функции y на отрезке [2, 5]:

6. Вычислить .

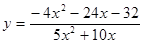; a = – 2.

Задание № 2

по теме "Интегральное исчисление"

1. Вычислить неопределенный интеграл

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл

7. Решить дифференциальное уравнение

8. Решить задачу Коши

Вариант № 3

Задание № 1

по теме "Дифференциальное исчисление"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

a = 3; а = – 3; а ® ¥.

2. Вычислить производную функций.

1).

2).

3. Вычислить y' в точке x₀: ; x₀= 2.

4. Найти экстремумы функции

5. Найти наибольшее и наименьшее значение функции y на отрезке [ – 6, – 3]:

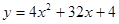
6. Вычислить : ; a = – 1.

Задание № 2

по теме "Интегральное исчисление"

1. Вычислить неопределенный интеграл

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл

7. Решить дифференциальное уравнение

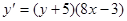
8. Решить задачу Коши

Вариант № 4

Задание № 1

по теме "Дифференциальное исчисление"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

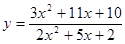a = – 3; а = – 2; а ® ¥.

2. Вычислить производную функций.

1).

2).

3. Вычислить y' в точке x₀: 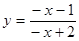; x₀= 0.

4. Найти экстремумы функции .

5. Найти наибольшее и наименьшее значение функции y на отрезке [ – 6, – 3]:

6. Вычислить : ; a = – 3.

Задание № 2

по теме "Интегральное исчисление"

1. Вычислить неопределенный интеграл

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл

7. Решить дифференциальное уравнение

8. Решить задачу Коши

Вариант № 5

Задание № 1

по теме "Дифференциальное исчисление"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

a = 2; а = 4; а ® ¥.

2. Вычислить производную функций.

1).

2).

3. Вычислить y' в точке x₀: ; x₀= – 5.

4. Найти экстремумы функции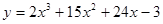

5. Найти наибольшее и наименьшее значение функции y на отрезке [ – 6, – 1]:

7. Вычислить : ; a = – 1.

Задание № 2

по теме "Интегральное исчисление"

1. Вычислить неопределенный интеграл

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл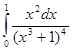

7. Решить дифференциальное уравнение

8. Решить задачу Коши

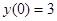
Вариант № 6

Задание № 1

по теме "Дифференциальное исчисление функции одной переменной"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

y = a = 2; а = 5; а ® ¥.

2. Вычислить производную функций.

1).

2).

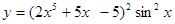
3. Вычислить y' в точке x₀.

; x₀= 3.

4. Найти экстремумы функции.

5. Найти наибольшее и наименьшее значение функции y на отрезке [ – 6, – 2]:

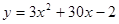
6. Вычислить .

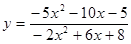; a = – 1.

Задание № 2

по теме "Интегральное исчисление функции одной переменной"

1. Вычислить неопределенный интеграл

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл

7. Решить дифференциальное уравнение

8. Решить задачу Коши

Вариант № 7

Задание № 1

по теме "Дифференциальное исчисление функции одной переменной"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

y = a = 1; а = – 4; а ® ¥.

2. Вычислить производную функций.

1).

2).

3. Вычислить y' в точке x₀.

; x₀= 5.

4. Найти экстремумы функции.

5. Найти наибольшее и наименьшее значение функции y на отрезке [2, 9]:

6. Вычислить .

; a = –3.

Задание № 2

по теме "Интегральное исчисление функции одной переменной"

1. Вычислить неопределенный интеграл

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл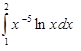

6. Вычислить определенный интеграл

7. Решить дифференциальное уравнение

8. Решить задачу Коши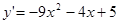

Вариант № 8

Задание № 1

по теме "Дифференциальное исчисление функции одной переменной"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

y = a = 5; а = – 5; а ® ¥.

2. Вычислить производную функций.

1).

2).

3. Вычислить y' в точке x₀.

; x₀=3.

4. Найти экстремумы функции.

5. Найти наибольшее и наименьшее значение функции y на отрезке [1, 8]:

6. Вычислить .

; a = 3.

Задание № 2

по теме "Интегральное исчисление функции одной переменной"

1. Вычислить неопределенный интеграл

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл

7. Решить дифференциальное уравнение

8. Решить задачу Коши

Вариант № 9

Задание № 1

по теме "Дифференциальное исчисление функции одной переменной"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

y = a = – 2; а = 1; а ® ¥.

2. Вычислить производную функций.

1).

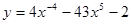
2).

3. Вычислить y' в точке x₀.

; x₀= – 5.

4. Найти экстремумы функции.

5. Найти наибольшее и наименьшее значение функции y на отрезке [2, 6]:

6. Вычислить .

; a = – 5.

Задание № 2

по теме "Интегральное исчисление функции одной переменной"

1. Вычислить неопределенный интеграл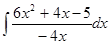

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл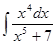

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл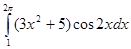

7. Решить дифференциальное уравнение

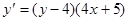
8. Решить задачу Коши

Вариант № 10

Задание № 1

по теме "Дифференциальное исчисление функции одной переменной"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя).

y = a = 2; а = – 1; а ® ¥.

2. Вычислить производную функций.

1).

2).

3. Вычислить y' в точке x₀.

; x₀= 4.

4. Найти экстремумы функции.

5. Найти наибольшее и наименьшее значение функции y на отрезке [–2, 2]:

6. Вычислить .

; a = 1.

Задание № 2

по теме "Интегральное исчисление функции одной переменной"

1. Вычислить неопределенный интеграл

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл

7. Решить дифференциальное уравнение

8. Решить задачу Коши

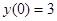
КОНТРОЛЬНАЯ РАБОТА №2

Вариант №1

Задание № 1

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: 2А – 3В.

2. Вычислить произведение матриц: .

3. Найти матрицу, обратную данной: A= .

4. Вычислить определитель, используя подходящее разложение по строке или столбцу: .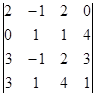

5. Вычислить ранг матрицы .

6. Решить систему линейных уравнений с помощью формул Крамера:

7. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 2

по теме "Теория вероятностей"

1. В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Из ящика вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.

2. В квадрат со стороной а вписана окружность. Какова вероятность того, что точка, появляющаяся случайным образом в пределах квадрата, окажется внутри круга?

3. В группе 12 студентов, среди которых 8 отличников. По списку вызывают 9 студентов. Найти вероятность того, что среди вызванных студентов окажется 5 отличников.

4. Круговая мишень состоит из 3-х зон. Вероятность попадания в I-ю зону - 0,15, во II-ю зону - 0,23, в III-ю зону - 0,17. Какова вероятность промаха?

5. В пирамиде установлено 5 винтовок, из которых 3 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.

6. Случайная величина задана рядом распределения:

x_i
р_i	0,01	0,25	0,35	0,26	0,13

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [1;3).

3) Определить числовые характеристики случайной величины: математическое ожидание (M_x), дисперсию (D_x), среднее квадратическое отклонение (s_x).

Вариант №2

Задание № 1

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: 3А – 2В.

2. Вычислить произведение матриц: .

3. Найти матрицу, обратную данной: A= .

4. Вычислить определитель, используя подходящее разложение по строке или столбцу

5. Вычислить ранг матрицы .

6. Решить систему линейных уравнений с помощью формул Крамера:

7. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 2

по теме "Теория вероятностей"

1. Брошен игральный кубик. Найти вероятность того, что выпадет четное число очков.

2. В броневом щите размером 2мх1м имеется невидимая для противника амбразура размером 0,1мх0,1м. Найти вероятность того, что пуля, попавшая в щит, попадает в амбразуру.

3. В группе из 30 слушателей на контрольной работе 6 слушателей получили оценку отлично, 10 слушателей - оценку хорошо. 9 слушателей – оценку удовлетворительно. Какова вероятность того, что все 3 слушателя, вызванных к доске, имеют неудовлетворительные оценки по контрольной работе?

4. Два стрелка, для которых вероятности попадания в мишень соответственно равны 0,7 и 0,8, производят по одному выстрелу по общей мишени. Определить вероятность поражения мишени.

5. В первой коробке содержится 20 радиоламп, из них 13 стандартных, во 2-й коробке - 10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.

6. Случайная величина задана рядом распределения:

x_i
р_i	0,01	0,15	0,35	0,26	0,23

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [0;3).

Вариант №3

Задание № 1

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: 3А + 2В.

2. Вычислить произведение матриц: .

3. Найти матрицу, обратную данной: A= .

4. Вычислить определитель, используя подходящее разложение по строке или столбцу

5. Вычислить ранг матрицы .

6. Решить систему линейных уравнений с помощью формул Крамера:

7. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 2

по теме "Теория вероятностей"

1. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

2. В круг радиусом R вписан равносторонний треугольник. Какова вероятность того, что поставленная внутри круга точка окажется и внутри треугольника.

3. Каждая из букв Т, М, Р, О, Ш написана на отдельной карточке. Карточки перемешиваются и раскладываются наудачу в ряд. Какова вероятность того, что образуется слово “ШТОРМ”?

4. Вероятность попадания бомбы в цель равна 0,4. С бомбардировщика сбрасывают 3 бомбы. Какова вероятность того, что: 1) ни одна не попадает в цель? 2) по крайней мере одна попадает в цель?

5. Вероятность попадания в мишень при одном выстреле р = 0,2. Найти количество патронов необходимых для поражения этой мишени с вероятностью, не меньшей 0,9.

6. Случайная величина задана рядом распределения:

x_i
р_i	0,11	0,20	0,30	0,36	0,03

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [10;30).

Вариант №4

Задание № 1

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: А – 2В.

2. Вычислить произведение матриц: .

3. Найти матрицу, обратную данной: A= .

4. Вычислить определитель, используя подходящее разложение по строке или столбцу

5. Вычислить ранг матрицы .

6. Решить систему линейных уравнений с помощью формул Крамера:

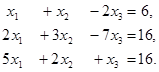
7. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 2

по теме "Теория вероятностей"

1. Брошено две монеты. Какова вероятность появления к гербов (к = 0, 1, 2)?

2. Грудная мишень, площадь которой S = 0,18м²,наклеена на прямоугольный щит размером 0,7мх0,6м. Найти вероятность того, что пуля, попавшая в щит, попадает в мишень, если попадание в любую точку щита равновозможно.

3. Для участия в шахматном турнире записалось 20 человек. Организаторы разбили участников на 2 команды по 9 человек. Какова вероятность того, что два наиболее сильных шахматиста будут играть в разных командах?

4. Три стрелка стреляют в одну мишень, при этом известно, что вероятности попадания с одного выстрела соответственно равны: 0,8; 0,7; 0,6. Найти вероятность появления в мишени одной пробоины в результате одновременного выстрела всех трех стрелков.

5. При разрыве снаряда образуются осколки крупные, средние и мелкие, причем число крупных, средних и мелких осколков составляет соотвественно: 0,2, 0,3 и 0,5 от общего числа осколков. При попадании в броню крупный осколок пробивает ее с вероятностью 0,7, средний – с вероятностью 0,4, мелкий – с вероятностью 0,005. Найти вероятность того, что броня будет пробита одним из осколков.

6. Случайная величина задана рядом распределения:

x_i
р_i	0,10	0,15	0,25	0,35	0,15

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [10;30).

3) Определить числовые характеристики случайной величины: математическое ожидание (Mx), дисперсию (Dx), среднее квадратическое отклонение (sx).

Вариант №5

Задание № 1

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: 2А – В.

2. Вычислить произведение матриц: .

3. Найти матрицу, обратную данной: A= .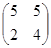

4. Вычислить определитель, используя подходящее разложение по строке или столбцу

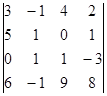5. Вычислить ранг матрицы .

6. Решить систему линейных уравнений с помощью формул Крамера:

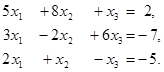
7. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 2

по теме "Теория вероятностей"

1. Брошено два игральных кубика. Найти вероятность того, что сумма очков на выпавших гранях равна семи.

2. Телефонная линия, соединяющая два пункта А и В, расстояние между которыми равно 7 км, оборвалась в неизвестном месте. Какова вероятность того, что место обрыва удалено от обоих пунктов далее чем на 2,5 км?

3. В ящике лежат 10 заклепок, отличающихся только материалом: 5 железных; 3 латунных и 2 медных. Наугад берут 2 заклепки. Какова вероятность того, что они будут из одного металла?

4. Производится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадания в первый склад 0,01; во второй 0,008; в третий 0,025. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны.

5. Что вероятнее, выиграть в шахматы у равносильного противника три партии из пяти или восемь из десяти?

6. Случайная величина задана рядом распределения:

x_i
P_i	0,20	0,35	0,15	0,26	0,04

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [2;4).

3) Определить числовые характеристики случайной величины: математическое ожидание (M_x), дисперсию (D_x), среднее квадратическое отклонение (d_x).

Вариант №6

Задание № 3

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: А – В.

2. Вычислить произведение матриц: .

3. Найти матрицу, обратную данной: A= .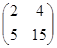

4. Вычислить определитель, используя подходящее разложение по строке или столбцу:

5. Вычислить ранг матрицы .

6. Решить систему линейных уравнений с помощью формул Крамера:

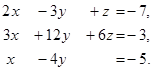
7. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 4

по теме "Теория вероятностей"

1. Бросается игральная кость. Какова вероятность того, что на верхней грани выпадает не более двух очков?

2. Какова вероятность того, что точка поставленная в квадрат со стороны а, окажется внутри вписанной в него окружности.

3. В ящике содержится 10 одинаковых деталей, помеченных номерами 1,2......10. Наудачу извлечено 6 деталей. Найти вероятность того, что среди извлеченных деталей окажется деталь № 1.

4. Три стрелка производят по одному выстрелу по мишени с вероятностями попадания 0,8; 0,9; О,7. Найти вероятность того, что:

а) в мишени нет пробоин; б) в мишени только две пробоины;

в) в мишени хотя бы одна пробоина.

5. Цель состоит из четырех отсеков и может быть поражена при попадании в первый отсек с вероятностью 0,2, при попадании во второй отсек – с вероятностью 0,3, при попадании в третий отсек – с вероятностью 0,92, при попадании в четвертый отсек с вероятностью 0,3. Вероятности попадания в каждый из отсеков равны соответственно 0,2; 0,3; 0,1; 0,4. Найти вероятность поражения цели при одном выстреле.

6. Случайная величина задана рядом распределения:

x_i
р_i	0,10	0,15	0,25	0,35	0,15

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [100;400).

Определить числовые характеристики случайной величины: математическое ожидание (Mx), дисперсию (Dx), среднее квадратическое отклонение (sx).

Вариант №7

Задание №1

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: –А +2В.

3. Вычислить произведение матриц: .

4. Найти матрицу, обратную данной: A= .

5. Вычислить определитель, используя подходящее разложение по строке или столбцу

6. Вычислить ранг матрицы .

7. Решить систему линейных уравнений с помощью формул Крамера:

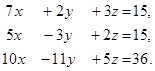
8. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 2

по теме "Теория вероятностей"

1. Слово "взвод" написано на отдельных карточках по одной букве на каждой. Карточки перевернуты и перемешаны. Какова вероятность выбрать наудачу карточку с написанной на ней: а) гласной буквой; в) буквой "в"?

2. В окружность радиуса R вписан квадрат. Найти вероятность того, что точка поставленная внутрь круга, не окажется в квадрате.

3. Технический контроль проверяет из партии в 100 деталей 20 деталей, взятых наудачу. Партия содержит 5 деталей нестандартных. Какова вероятность того, что среди проверяемых деталей будет ровно две нестандартные?

4. Три курсанта производят по одному выстрелу по мишени с вероятностью попадания в мишень 0,8; 0,9; 0,7. Найти вероятность следующих событий:

а) в мишени 3 пробоины; б) в мишени пробоин нет; в) в мишени только две пробоины;

г) в мишени хотя бы одна пробоина.

5. Имеется три урны с шарами. В первой урне 7 белых и три черных шара, во второй – один белый и девять черных шаров, в третьей – девять белых и один черный шар. Какова вероятность того, что шар из наудачу взятой урны – черный?

6. Случайная величина задана рядом распределения:

x_i
р_i	0,12	0,28	0,20	0,30	0,10

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [2;6).

3) Определить числовые характеристики случайной величины: математическое ожидание (Mx), дисперсию (Dx), среднее квадратическое отклонение (sx)

Вариант № 8

Задание № 1

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: –2А + 3В.

3. Вычислить произведение матриц: .

4. Найти матрицу, обратную данной: A= .

5. Вычислить определитель, используя подходящее разложение по строке или столбцу

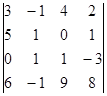6. Вычислить ранг матрицы .

7. Решить систему линейных уравнений с помощью формул Крамера:

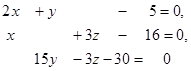
8. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 2

по теме "Теория вероятностей"

1. В лотерее 5000 билетов, из них 6 выигрышных. Какова вероятность выиграть, купив один билет?

2. Телефонная линия, соединяющая два пункта А и В, отстоящих друг от друга на расстоянии 2 км, порвалась в неизвестном месте. Чему равна вероятность того, что она порвалась не далее, чем в 450 м от пункта А?

3. На складе имеется 15 кинескопов, причем 10 из них изготовлено Львовским заводом. Найти вероятность того, что среди наудачу взятых пяти кинескопов окажется 3 кинескопа Львовского завода.

4. Бомбардировщик последовательно преодолевает три зоны ПВО. При проходе первой зоны он поражается с вероятностью 0,6; второй (при условии прохождения первой зоны) – с вероятностью 0,7 и третьей (при условии прохождения первых двух) – с вероятностью 0,5. Определить вероятности:

а) преодоления всех трех зон; б) поражения бомбардировщика при проходе второй зоны.

5. В инспекторских стрельбах участвуют 30 стрелков, из которых 15 отличных стрелков могут выполнить стрельбу с вероятностью 0,9; 8 хороших стрелков – с вероятностью 0,8; 4 удовлетворительных стрелка – с вероятностью 0,5, 3 слабых стрелка – с вероятностью 0,3. Какова вероятность выполнения задачи наудачу вызванным стрелком?

6. Случайная величина задана рядом распределения:

x_i
P_i	0,20	0,25	0,35	0,25	0,05

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [12;32).

Вариант № 9

Задание № 1

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: 5А – 2В.

2. Вычислить произведение матриц: .

3. Найти матрицу, обратную данной: A= .

4. Вычислить определитель, используя подходящее разложение по строке или столбцу

5. Вычислить ранг матрицы .

6. Решить систему линейных уравнений с помощью формул Крамера:

7. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 2

по теме "Теория вероятностей"

1. Вычислить вероятность того, что при бросании двух игральных костей сумма очков составит восемь.

2. Самолет-снаряд с равной вероятностью может упасть в любой точке на территории завода площадью 15 кв. км. Какова вероятность попадания в заводские корпуса общей площадью 5кв.км.?

3. По данным ОТК на 20 металлических брусков, заготовленных для обработки, приходится 3 с зазубринами. Какова вероятность, что случайно взятые 2 бруска будут с дефектом?

4. Вероятность попадания в цель при одном выстреле 0,3. Стрельба ведется одиночными выстрелами до первого попадания. Какова вероятность прекращения стрельбы после пятого выстрела?

5. Стрелок производит 5 независимых выстрелов, по мишени. Вероятность попадания в цель при каждом выстреле р = 0,3. Найти вероятность того, что при пяти выстрелах произойдет: 1) два попадания 2) хотя бы одно попадание.

6. Случайная величина задана рядом распределения:

x_i
P_i	0,12	0,28	0,24	0,26	0,10

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [10;30).

Вариант № 10

Задание № 1

по теме "Линейная алгебра"

1. Вычислить линейную комбинацию матриц А и В:

Дано: , . Найти: 4А – 3В.

3. Вычислить произведение матриц: .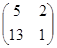

4. Найти матрицу, обратную данной: A= .

5. Вычислить определитель, используя подходящее разложение по строке или столбцу

6. Вычислить ранг матрицы .

7. Решить систему линейных уравнений с помощью формул Крамера:

8. Методом Гаусса исследовать совместность и найти общее решение системы:

Задание № 2

по теме "Теория вероятностей"

1. В урне 5 белых и 3 черных шара. Из урны вынимают один шар. Найти вероятность того, что шар черный.

2. В круг вписан квадрат. Какова вероятность того, что точка, брошенная наудачу внутрь круга, не попадет в квадрат?

3. Имеется 30 патронов, из которых один с трассирующей пулей. Наудачу взято 20 патронов. Какова вероятность того, что среди них окажется патрон с трассирующей пулей?

4. Ведется стрельба из четырехорудийной батареи. Вероятность попадания в цель при стрельбе из первого орудия – 0.2; из второго орудия – 0,4; из третьего – 0,3; из четвертого орудия – 0,3. Определить вероятность попадания при одном выстреле, если равновероятна стрельба из любого орудия.

5. Вероятность попадания при одном выстреле р = 0,4. Какова будет вероятность четырех попаданий при восьми выстрелах, 2-х попаданий при десяти выстрелах?

6. Случайная величина задана рядом распределения:

x_i
P_i	0,02	0,18	0,30	0,35	0,15

1) Найти функцию распределения F(x) и построить ее график.

2) Найти вероятность попадания случайной величины в интервал [1;3).

Основные термины и определения

1. Математика – наука о количественных отношениях и пространственных формах действительного мира.

2. Дедукция – (лат. deductio – выведение) – логическое умозаключение от общего к частному, от общих суждений к частным или другим общим выводам.

3. Индукция – логическое умозаключение от частных, единичных случаев к общему выводу, от отдельных фактов к обобщениям. Или: индукция – способ математических доказательств и определений, основанный на переходе от заключения, верного для некоторого натурального числа n, к заключению, верному для числа (n +1).

4. Аналитическая геометрия – раздел геометрии, в котором простейшие геометрические образы (прямые, плоскости, линии, поверхности) исследуются средствами алгебры на основе метода координат. Каждой линии на плоскости соответствует свое уравнение, работа с уравнениями осуществляется аналитическими и алгебраическими средствами.

5. Линейная алгебра – обобщение аналитической геометрии на случай n-мерных векторных пространств.

6. Матрицей размера mxn называется совокупность m n выражений, расположенных в виде прямоугольной таблицы из m строк и n столбцов.

7. Квадратной матрицей порядка n называется матрица, в которой m = n, т.е. число строк равно числу столбцов.

8. Матрицей-строкой (вектор строкой) называется матрица размером, состоящая из одной строки.

9. Матрицей-столбцом (вектор строкой) называется матрица размером, состоящая из одного столбца.

10. Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается 0 или (0)_mxn (в алгебре матриц эта матрица играет роль нуля).

11. Квадратнаяматрица, в которой отличны от нуля только