Часто при моделировании физических процессов и явлений получаются уравнения, которые содержат функции нескольких переменных и частные производные от этих функций. Такие уравнения называются уравнениями с частными производными (или уравнения в частных производных).
Приведем примеры уравнений второго порядка с частными производными разных типов:
– волновое уравнение (гиперболическое)
 ;
;
– уравнение теплопроводности или диффузии (параболическое)
 ,
,  ;
;
– уравнение Пуассона (эллиптическое)
 .
.
Если правая часть последнего уравнения равна нулю  , то оно называется уравнением Лапласа.
, то оно называется уравнением Лапласа.
Решение дифференциальных уравнений рассматривается, как правило, для систем, ограниченных в пространстве и в течение конечного промежутка времени. Следовательно, решение уравнения ищется в ограниченной, в данном случае прямоугольной, области G:
 . (1)
. (1)
Для получения частного решения параболического уравнения (уравнения теплопроводности) необходимо задать одно начальное условие и два граничных. Начальное условие может быть задано в виде
 ,
,  , (2)
, (2)
где 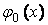 – заданная функция, определяющая значение функции
– заданная функция, определяющая значение функции 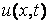 в начальный момент времени
в начальный момент времени  .
.
Граничные условия задают значения функции 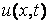 при
при  и
и  могут иметь, например, следующий вид:
могут иметь, например, следующий вид:
 ,
,  ,
,  , (3)
, (3)
где  и
и  – заданные функции.
– заданные функции.
Например, если 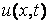 – температура тонкого однородного стержня длинной l, то условия (2) задает начальное значение температуры каждой точки стрежня при
– температура тонкого однородного стержня длинной l, то условия (2) задает начальное значение температуры каждой точки стрежня при  , а условия (3) означают, что температура в начале и конце стержня задана в каждый момент времени, в частности, поддерживается постоянной
, а условия (3) означают, что температура в начале и конце стержня задана в каждый момент времени, в частности, поддерживается постоянной  и
и  .
.
Геометрической интерпретацией искомого решения 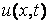 является поверхность в пространстве
является поверхность в пространстве  , которая проецируется на область G плоскости
, которая проецируется на область G плоскости  , причем в соответствии с (2) и (3) заданы три кривые, которые представляют собой края этой поверхности (рис. 7.1). Внутри области G значения функции
, причем в соответствии с (2) и (3) заданы три кривые, которые представляют собой края этой поверхности (рис. 7.1). Внутри области G значения функции 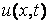 неизвестны, поэтому неизвестна форма поверхности и ее требуется найти путем решения начально-краевой нестационарной задачи.
неизвестны, поэтому неизвестна форма поверхности и ее требуется найти путем решения начально-краевой нестационарной задачи.
Для обеспечения единственности решения уравнения гиперболического типа (волнового уравнения) необходимо задать два начальных условия и два граничных условия. Начальные условия, как правило, задаются в виде:
 ,
,  ,
,  , (4)
, (4)
где 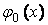 и
и  – заданные функции, определяющие значение функции
– заданные функции, определяющие значение функции 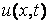 и ее первой производной по t в начальный момент времени
и ее первой производной по t в начальный момент времени  . Граничные условия задаются аналогично (3). Геометрически решению данной начально-краевой задачи соответствует поверхность в пространстве
. Граничные условия задаются аналогично (3). Геометрически решению данной начально-краевой задачи соответствует поверхность в пространстве  (рис. 7.1).
(рис. 7.1).
Наиболее распространенными и универсальными среди численных методов для решения уравнений с частными производными являются разностные (сеточные) методы. Как и в случае решения обыкновенных дифференциальных уравнений в их основе лежит идея дискретизации задачи и замене частных производных, которые входят в уравнения, их приближенными разностными отношениями. При этом исходное дифференциальное уравнение заменяется системой алгебраических уравнений, называемой разностной схемой. Решая эту систему можно найти в узлах сетки значения сеточной функции, которые приближенно считаются равными значениям искомой функции.
 В случае прямоугольной области G расчетная сетка строится следующим образом (рис. 7.2). Отрезок
В случае прямоугольной области G расчетная сетка строится следующим образом (рис. 7.2). Отрезок  на оси x разбивается на n равных частей длины
на оси x разбивается на n равных частей длины  , при этом получается
, при этом получается  узловых точек
узловых точек  ,
,  . Аналогично отрезок
. Аналогично отрезок  на оси y разбивается на m равных частей длины
на оси y разбивается на m равных частей длины  , при этом получается
, при этом получается  узловых точек
узловых точек  ,
,  . Проводя через эти точки прямые, параллельные осям координат, получаем сетку, разбивающую область G на элементарные прямоугольные ячейки. Любой узел сетки, номер которого
. Проводя через эти точки прямые, параллельные осям координат, получаем сетку, разбивающую область G на элементарные прямоугольные ячейки. Любой узел сетки, номер которого  , определяется координатами
, определяется координатами  . Решение задачи ищется именно в этих точках. Поскольку все ячейки построенной сетки одинаковы, такую сетку называют равномерной. Узлы сетки, лежащие на границе области G, называются граничными узлами; все остальные узлы – внутренними.
. Решение задачи ищется именно в этих точках. Поскольку все ячейки построенной сетки одинаковы, такую сетку называют равномерной. Узлы сетки, лежащие на границе области G, называются граничными узлами; все остальные узлы – внутренними.
Аналогично вводятся сетки и для многомерных областей, содержащих более двух измерений.
Для построения разностной схемы, как и в случае обыкновенных дифференциальных уравнений, частные производные в уравнении приближенно заменяются конечно-разностными отношениями. При этом точные значения искомой функции заменяются значениями сеточной функции в узлах сетки.
Уравнение теплопроводности. Уравнение параболического типа возникает при рассмотрении так называемых явлений переноса, при которых происходят процессы передачи теплоты, массы, количества движения. В частности, к явлениям переноса относятся теплопроводность, диффузия, внутреннее трение. Рассмотрим типичную постановку начально-краевой задачи для одномерного уравнения теплопроводности, описывающего, например, распространение тепла в однородном стержне постоянного сечения:
 ,
,  ,
,  ,
,  ,
,
(5)
 ,
,  ,
,  ,
,
где  – начальное распределение температуры U вдоль стержня (при
– начальное распределение температуры U вдоль стержня (при  );
);  ,
,  – значения температуры на концах стержня в любой момент времени t. Коэффициент a определяется теплопроводностью k и удельной теплоемкостью l материала стержня (
– значения температуры на концах стержня в любой момент времени t. Коэффициент a определяется теплопроводностью k и удельной теплоемкостью l материала стержня (  ). Заметим, что начальные и граничные условия должны быть согласованы, т.е.
). Заметим, что начальные и граничные условия должны быть согласованы, т.е.  ,
,  .
.
Введем равномерную сетку с помощью координатных линий  (
(  ),
),  (
( 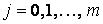 ); h и t – шаги сетки по направлениям x и t, соответственно. Значения искомой функции в узлах сетки обозначим
); h и t – шаги сетки по направлениям x и t, соответственно. Значения искомой функции в узлах сетки обозначим  . Эти значения заменим соответствующими значениями сеточной функции
. Эти значения заменим соответствующими значениями сеточной функции  , которые удовлетворяют уравнениям, образующим разностную схему.
, которые удовлетворяют уравнениям, образующим разностную схему.
Заменим в уравнении (5) частные производные искомой функции приближенными разностными отношениями:
 ,
, 
Подстановка этих соотношений в (5) дает систему разностных уравнений для внутренних узлов сетки
 ,
,
(6)
 ,
, 
Значения сеточной функции в граничных узлах сетки определяются начальными и граничными условиями:
 ,
,  ,
,
(7)
 ,
,  ,
, 
Соотношения (6) в совокупности с дополнительными условиями (7) образует замкнутую систему уравнений называемую разностной схемой.
Совокупность узлов при фиксированном значении j называется слоем (в данном случае временн ы м слоем).
Схема (7.10) позволяет последовательно находить значения  (
(  ) на
) на  -м слое через соответствующие значения
-м слое через соответствующие значения  на j -том слое:
на j -том слое:
.
 (
( ) (8)
) (8)
Если функция в правой части уравнения не равна нулю, то соотношение (8) примет следующий вид:
 (
( )+
)+  (9)
(9)
Рассмотренная выше явная разностная схема (6) является условно устойчивой. Можно показать, что решение будет устойчивым только при выполнении условия
 . (10)
. (10)
Задание: Решить параболическое уравнение описывающее распределение температуры в,
стержне длиной L=5 на временном интервале Т=2, начальная температура стержня задается произвольной функцией
φ(x)=exp(0.15x). Температуры концов стержня равны  .
.

Задаются параметры: L (длина стержня),T (временой интервал), N (число разбиений по длине),K (число разбиений по времени), a (коэффициент температуропроводности),  .
.
На выходе: вектора x,t и матрица решений u






