Обработка результатов измерений

Цель работы:

1. Экспериментальное определение формы эквипотенциальных поверхностей в моделях плоского и цилиндрического конденсаторов.

2. Расчет напряжённости электростатического поля по найденному распределению потенциала.

3. Проверка теоретических предсказаний относительно координатной зависимости потенциала для обеих моделей.

Теоретические основы лабораторной работы:

Взаимодействие между неподвижными электрически заряженными телами осуществляется посредством электрического поля. При этом каждое заряженное тело создает в окружающем пространстве поле, воздействующее на другие заряженные тела, и само это тело испытывает на себе воздействие электрических полей, созданных окружающими телами. Если заряды-источники неподвижны, то их электрическое поле стационарно, т.е. не изменяется с течением времени. Такое поле называют электростатическим. Силовой характеристикой электрического поля служит вектор его напряженности. Этот вектор в данной точке пространства определяется соотношением

, (1)

где – сила, действующая на неподвижный заряд q, помещенный в данную точку. Заряд q в формуле (1), с помощью которого детектируется электрическое поле, называется «пробным». Для графического изображения электростатических полей используют силовые линии. Силовыми линиями (линиями напряженности) называют линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности в этой точке. Силовые линии электростатического поля разомкнуты. Они начинаются на положительных зарядах и оканчиваются на отрицательных зарядах (в частности, они могут уходить в бесконечность или приходить из бесконечности).

Энергетической характеристикой электрического поля является его потенциал. Потенциалом в данной точке поля называется скалярная величина

, (2)

где – потенциальная энергия заряда 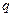, помещенного в данную точку. При перемещении заряда 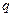из точки с потенциалом в точку с потенциалом силы электростатического поля совершают над зарядом работу

. (3)

Геометрическое место точек, в которых потенциал имеет одинаковую величину, называется эквипотенциальной поверхностью.

Напряженность и потенциал электростатического поля связаны друг с другом соотношениями

, (4)

. (5)

Вектор градиента (градиент) потенциала в формуле (4) определяется через частные производные потенциала по декартовым координатам x, y, z:

. (6)

Здесь , , – единичные вектора положительных направлений (орты) координатных осей , , 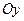. Направление градиента потенциала в данной точке совпадает с направлением быстрейшего возрастания потенциала, а его величина равна быстроте изменения потенциала на единицу перемещения в этом направлении. Направление вектора напряженности электростатического поля в соответствии с формулой (4) противоположно направлению градиента. Следовательно, вектор напряженности направлен в сторону наибыстрейшего убывания потенциала. Кроме того, из формулы (5) следует, что вектор перпендикулярен к эквипотенциальной поверхности в любой ее точке.

Если известны потенциалы и двух точек, лежащих на одной силовой линии (см. рис.1), то средняя напряженность между этими точками вычисляется по формуле

, (7)

где – длина участка силовой линии между точками. Если относительное изменение локального значения напряженности между выбранными точками невелико, то формула (7) дает значение близкое к напряженности на середине участка .

В лабораторной работе исследуется пространственное распределение потенциала и напряженности электростатического поля для двух плоских моделей, в одной из которых электростатическое поле совпадает с полем плоского конденсатора, в другой – с полем цилиндрического конденсатора. Внутри плоского конденсатора вдали от краев пластин электрическое поле однородно (), и потенциал равномерно возрастает при движении вдоль координатной оси от отрицательной обкладки к положительной по формуле

, (8)

где 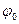–потенциал отрицательной пластины, –модуль вектора электрической напряженности.

Внутри цилиндрического конденсатора модуль электрической напряженности спадает обратно пропорционально расстоянию от оси ( ~ ), и, если внутренняя обкладка заряжена отрицательно, потенциал изменяется в соответствии с формулой

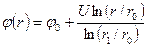, (9)

где 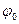– потенциал внутренней обкладки; – разность потенциалов между обкладками; , – радиусы внутренней и внешней обкладок соответственно.

Описание установки.

Приборы и принадлежности, используемые в лабораторной работе, показаны на рисунке. Для питания моделей используется стабилизированный источник постоянного напряжения. Для измерения потенциала – цифровой вольтметр с большим внутренним сопротивлением (не менее 1Мом). Для исследования распределения потенциала в обеих моделях используется плоские планшеты. В каждом планшете на изолирующей жесткой подложке наклеены металлические электроды из медной фольги и слой проводящей бумаги между электродами. Для подсоединения к источнику питания, каждый планшет снабжен проводами с однополюсными вилками на концах (на рисунке не показаны). Координаты щупа на планшете, моделирующем плоский конденсатор, измеряются с помощью вертикальной шкалы самого планшета и дополнительной миллиметровой линейки. Планшет, моделирующий электрическое поле цилиндрического конденсатора, снабжен угловой градусной шкалой. Для определения радиальной координаты в этой модели используется своя миллиметровая линейка, со шкалой идущей от центра в обе стороны. В комплект также входят соединительные провода, и щуп со скругленным концом. При выполнении работы одним из проводов соединяет гнездо «*» (общую клемму) вольтметра с клеммой «минус» источника питания, другой провод используется для подключения щупа к вольтметру.

Бумага, используемая в моделях, имеет значительное удельное сопротивление по сравнению с удельным сопротивлением медной фольги, из которой изготовлены электроды – «обкладки» модельных конденсаторов. Токи, текущие в бумаге, не сильно искажают распределение зарядов на электродах. Поэтому величина и направление вектора напряженности между электродами оказываются такими же, как в вакууме, а распределение потенциала в модели повторяет соответствующее распределение для оригинала. Подключая вольтметр с достаточно большим входным сопротивлением к одному из электродов и к произвольной точке бумаги, мы можем измерить разность потенциалов между этой точкой и электродом. Сопротивление вольтметра должно быть велико по сравнению с сопротивлением бумаги, для того чтобы измерительный ток вольтметра не шунтировал токи в модели и не искажал распределение электрического поля.

Результат измерений.

Упражнение1.

1) = 10 В

= 0,1 А

= 20 В

= 180 мм

= 185 мм

= 0 В

= 10 В

= 0,05 В

1 мм

2)

№ точки	В	см
мм

3) 5,5 см

Таблица 1. Зависимость потенциала от координаты для модели плоского конденсатора.

№ точки
см
В	1,15	2,35	3,40	4,45	5,50	6,60	7,65	8,80

Упражнение2.

1) = 10 В

= 0,1 А

1 мм

9 мм

91 мм

1 мм

2)

№ точки	В
мм

3)

Таблица 2. Зависимость потенциала от координаты для модели цилиндрического конденсатора.

№ точки
мм
В	1,50	2,40	2,90	3,90	4,70	5,40	6,00	7,10	8,00	9,40

Обработка результатов измерений.

1. На обоих листах миллиметровой бумаги с отмеченными точками проведём эквипотенциальные линии, соединив точки с равным потенциалом.

2. Для модели плоского конденсатора из точек с координатами = 0, = 1; 3; 5; 7; 9; 11; 13; 15; 17 см перпендикулярно к потенциальным линиям проведём силовые линии от одного электрода до другого.

3. По формуле (7) из данных таблицы 1 вычислим среднюю напряженность электростатического поля между точками

1-2: ,

3-4: ,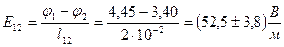

5-6: ,

7-8: .

4. Выведем формулу для расчета погрешности 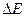и вычислить погрешности для значений, найденных в п.3.

5. По данным таблицы 1 построим график зависимости 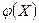потенциала от координаты в плоском конденсаторе (нанесём точки и построим аппроксимирующую прямую).

6. Для модели цилиндрического конденсатора из точек на границе внутреннего электрода с угловыми координатами = 0°; 45°; 90°; 135°; 180°; 225°; 270°; 315° перпендикулярно к потенциальным линиям проведём силовые линии до внешнего электрода.

7. По данным таблицы 2 построим график зависимости потенциала от координаты в цилиндрическом конденсаторе (нанесём точки и построим аппроксимирующую гладкую кривую). Определим графически угловой коэффициент наклона касательной к графику в точках с координатами = 20; 40; 60; 80 мм. Найденные значения углового коэффициента, как следует из формулы (4) равны значениям напряженности при заданных .

20 мм: ,

40 мм: ,

60 мм: ,

80 мм: .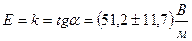

8. Выведем формулу для расчета погрешности и вычислим её для найденных в п.7. значений углового коэффициента. Так как величина выводится графически через построение касательной к графику , то основная погрешность приходится на невозможность точного построения с помощью циркуля, уголка и линейки. Также важна погрешность измерения. Определим приборную погрешность и выведем погрешность напряжённости

9. По данным таблицы 2 заполним таблицу 3.

Таблица 3. Зависимость потенциала от величины для модели цилиндрического конденсатора.

№ точки
	0,51	0,69	0,80	1,02	1,20	1,36	1,49	1,71	1,90	2,18
В	1,50	2,40	2,90	3,90	4,70	5,40	6,00	7,10	8,00	9,40

10. По данным таблицы 3 построим график зависимости потенциала от величины (нанесём точки и построим аппроксимирующую прямую). Эта зависимость прямолинейная, что соответствует формуле (9).

Вывод.

Мы экспериментально определили формы эквипотенциальных поверхностей в моделях плоского и цилиндрического конденсаторов, отобразив их на листе миллиметровой бумаги, рассчитали числовое значение напряжённости электростатического поля по найденному распределению потенциала и её погрешность и проверили теоретические предсказания относительно координатной зависимости потенциала для обеих моделей. Так как по графикам зависимость потенциала от величины для модели цилиндрического конденсатора и зависимость потенциала от величины для модели плоского конденсатора прямолинейные, то теоретические предсказания верны.