Лабораторная работа №2
Программирование разветвлений
1. Цель работы:
1.1.;
ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ
2.1. Изучить теоретический материал
2.2. Проделать практическое задание
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Стандартные арифметические функции
В арифметических выражениях часто используются следующие стандартные функции (табл. 1)
Таблица 1. Некоторые стандартные функции, типы значений аргумента и результата
| Стандартная функция | Выполняемое действие | Тип | |
| Аргумента | Результата | ||
| abs(x) | | x | | real | Real |
| integer | integer | ||
| sqr(x) | X2 | real | Real |
| integer | integer | ||
| sqrt(x) | X1/2 | real | Real |
| integer | Real | ||
| exp(x) | ex | real | Real |
| integer | Real | ||
| Ln(x) | Ln(x) | real | Real |
| integer | Real | ||
| Pi | число пи | — | Real |
| sin(x) | Sin(x) | real | Real |
| integer | Real | ||
| cos(x) | Cos(x) | real | Real |
| integer | Real | ||
| arctan(x) | arctg(x) | real | Real |
| integer | Real |
Вызов стандартной функции осуществляется путем указания в нужном месте программы имени функции (abs, ln, exp и др.) и ее аргумента, заключенного в круглые скобки. После вычисления значения функции ее вызов заменяется результатом, и расчет содержащего ее выражения продолжается дальше.
Примечание:
1 аргумент прямых тригонометрических функций sin и cos задается в радианах. Для преобразования значения угла из радианной меры в градусную необходимо умножить величину угла на число 180/pi. Для перевода значения угла из градусной меры в радианную необходимо умножить величину угла на число pi/180;
Результат функции arctan получается в радианах.
Кроме приведенных в табл. 1, в арифметических выражениях также используются следующие стандартные функции:
1 функция random (диапазон) возвращает случайное число x, удовлетворяющее условию 0<=x<диапазон. Тип аргумента и результата — word. В том случае, если нам необходимы целые случайные числа из диапазона a<=x<b, мы можем получить их, используя выражение random(b‑a)+a. Если параметр диапазон не указан, то random возвращает число x в диапазоне 0<=x<1. Тип результата — real. В том случае, если нам необходимы вещественные случайные числа из другого диапазона: a<=x<b, мы можем задать его при помощи random*b+a. Перед первым обращением к функции random необходимо с помощью вызова процедуры randomize инициализировать программный генератор случайных чисел. В противном случае при каждом запуске программы датчик будет выдавать одни и те же числа. Эту особенность можно использовать при отладке программы;
функция frac(x) вычисляет дробную часть x. Аргумент и результат — real. Например, write(frac(0.25*11):4:2); {результат 0.75};
функция int(x) вычисляет целую часть x. Аргумент и результат — real. Например, write(int(422.117):4:2); {результат 422.00}; Таким образом, x=int(x)+frac(x).
Полезные формулы
Возведение в степень
Вычисление степени числа выполняется в Pascal с использованием свойств логарифмов:
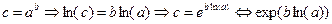
Таким способом нельзя возвести в степень отрицательное число. Можно возвести в степень модуль этого числа, а знак обработать отдельно.
Логарифм с произвольным основанием
Для вычисления логарифма с основанием a используем:







