Анализ зависимости частот колебаний ЛА от массы топлива ракеты

Лабораторная работа 1, 2, 3

по дисциплине «Динамика и прочность ракетных двигателей»

Тема: «Анализ зависимости частот колебаний ЛА от массы топлива ракеты, от геометрических характеристик ракетного двигателя»

 

 

Выполнил студент гр. ЛА-08	Наугольных Д. А.
Проверил профессор	Сальников А.Ф.

 

Пермь, 2012

 

Цель работы:

1. Провести анализ частотных характеристик, изменяя массу топлива на 20 %.

2. Провести анализ частотных характеристик, изменяя массу корпуса на 20 %.

3. Провести анализ частотных характеристик, изменяя массу корпуса и топлива на 20 %, тем самым изменяя длину ЛА.

 

Теоретические сведения

Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Два основных подхода в изучении колебаний элементов и узлов машин:

Первый:

Связан с формированием вектора колебательного движения с использованием Максвеловского подхода:

(1)

- матрицы ускорения, скоростей и перемещения элементов системы.

[m]- массовые характеристики.

[L]- матрица конструктивной вязкости.

[C]- матрица жесткости.

[F]- столбец внешних сил.

-матрица силовых связей элементов систем.

Уравнение в общем виде (1), формирует общую базу математического описания колебательной системы в общем виде из которого можно получить записи собственных, вынужденных, парциальных колебаний.

Любое колебательное движение системы содержит в себе собственные колебания и вынужденные колебания, которые будут определяться правой частью уравнения (1). Основными параметрами любого колебательного процесса является период, амплитуда, длина волны.

Виды колебаний:

1. Собственные - это когда в уравнении (1), элементы 2,4,5 равны 0, следовательно: .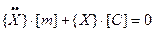

2. Затухающие - когда в уравнении (1), элементы 4,5 равны 0.

3. Вынужденные - это такие колебания системы, когда в уравнении (1), элемент 5, равен 0, следовательно:

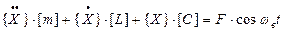
Количество вынужденных колебаний, равно количеству вынужденных сил:

.

i= (1÷n).

Второй:

Метод распределенной массы. Каждый элемент имеет пространственную систему распределения массы: m(x), m(y),m(z)

Каждая из сечений s связаны между собой внутренними силами, которые зависят от момента инерции и модуля материала.

В связи с этим сформирован основной подход.

Данный метод позволяет просматривать продольные, крутильные и изгибные колебания.

1. Продольные колебания смещения относительно положения равновесия.

2. Изгибные колебания – относительное смещение сечения с его поворотом сечения относительно его равновесия.

3. Кручение – поворот относительной оси.

Таким образом, структура колебательного движения жестко предполагает формирования таких, которые могут существовать в изделии в той или иной форме. Полагая при этом, что колебания не зависимы друг от друга.

Продольные колебания

А=a sin 𝜔t

 

 

Рассмотрим параллельное смещение:

S1-продольная волна. Эффект сжатия называют продольной волной,которая распространяется со скоростью звука либо выше.

· Если ниже скорости звуко-механические колебания;

· Если выше скорости звуко-ударная волна;

 

-m(x)* =f(xt)

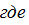f(xt)-внешняя нагрузка которая приводит к смещению сечения при определенном воздействии. Если предполагать, что f(xt) –это кратковременное воздействие, то

-m(x)* =0 (2)

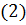-уравнение собственных колебаний элемента;

 

Чтобы найти характер смещения необходимо ввести следующие понятия: φ(х)-функция смещения (закон изменения смещения относительно равновесия), Ψ(х)функционал смещения, определяет в первом приближении амплитуду смещения; функционал зависит от массы и положения. Следовательно, u –смещение точки в сечении.

u (xt)= φ sin () (3),

где н-индекс смещения; φ- форма; -изменение формы.

Выражение (3) подставляем в (2) и получаем:

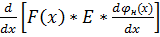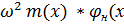=- ), (4)-функция смещения

 

Для того чтобы решить уравнение нужно взять интеграл на границах. На границах производная при х=0 и х=L.Получаем,

= 0

Смещение есть, а скорости нет в данном месте. Нужно взять интеграл от (4) полагая, что х- постоянная величина. Аналитическое решение (4) может быть решено приближенно. Есть 2 случая когда уравнение решено:

1) Ψ(х)-когда задано;

2) M(x) есть величина постоянная u=x

Возьмем интеграл из выше указанных условий, тогда

=- (5)

В это случае (5) можно решить только тогда, когда будет известна функция смещения .

После второго интегрирования необходимо, что функция совпадала с первой. Для этого введем нормирующий функционал.

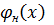=-𝜔 + (6),

где -постоянная интегрирования;

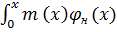= = dx, тогда =

После постоянного интегрирования получаем:

=

Выбранная функция будет зависеть от частоты: 𝜔 =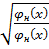

Для возникновения продольных колебаний необходимо осевые силы, которые сжимают(растягивают) конструкцию.

Изгибные колебания.

𝜔 – характеристика прогиба, конструктивного элемента, под действием периодической силы перпендикулярной продолжению оси объекта.

В допущениях величина осевого смещения при колебаниях будем считать равным нулю.

Изгибные колебания будем рассматривать как поворот при ортогональном смещении. Изгиб оси симметрии связан с моментом.

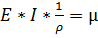(1)

где текучий радиус изгиба

Е – модуль упругости

I – момент инерции

Для того чтобы учесть изменения момента инерции относительно оси изгиба предполагается его интегральное значение.

Радиус прогиба элемента будет определяться как:

Так как в силу малости смещения знаменатель стремится к 1 и получаем формулу.

Уравнение (3) связывает изгибающий момент с функцией прогиба.

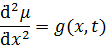
Получаем

()= (4)

- инерционная массовая нагрузка,связанная с инерцией смещения поперечной массы.

и (5)

()+m * = (6)

(5)- уравнение движения при изгибе объекта относительно его продольной оси.

(6) – описывает изменение во t смещения по оси n по времени.

Будем полагать что:

()+m * =0 (7)

(7) – собственные колебания тел.

Подразделение переменной позволит нам получить новую формулу выражения (7).

W(x,t)= 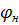(x) (8) - функция прогиба

Тогда первая производная функции смещения в точке x=0 и x=L от сюда следует, что W=0

Данное утверждение позволяет (7) с учетом (8) переписать в новом виде:

()- m )=0 (9)

W(x,t)= )*cos (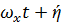) (10)

ή – фазовый угол смещения функции преобразования прогиба оси объекта при изгибных колебаниях.

Исходя из физики взаимодействия частот по модам будем раздельно рассматривать условие возникновения колебательных движений при изгибе объекта.

f (n)=

dx=1

Использование нормирования форм колебаний четко позволяет в отличии от продольных колебаний получить моду(тон).

 

Крутильные колебания

В случае крутильных колебаний собственные частоты не образуют гармонического ряда, т.к. скорость распространения крутильных волн зависит от частоты.

 

Исходные данные

Количество ступеней:
Диметр Миделя, м:	1,6
Количество форм колебаний:
Шаг по длине ЛА, м:	0,001
Точность расчета, Гц:
Материал корпуса:	Боропластик

 

Характеристики топлива №2

	- плотность топлива
	- температура в КС
	- газовая постоянная ПС
	- показатель в законе горения
	- коэффициент в законе горения
	- единичный импульс топлива

 

 

Анализ зависимости частот колебаний ЛА от массы топлива ракеты

1) Увеличим массу топлива на 20%.

Рис.1.1.1 Изгибные колебания

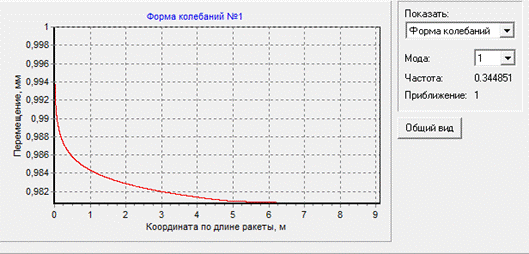
Рис.1.1.2 Продольные колебания

Рис.1.1.3 Крутильные колебания

2) Уменьшим массу топлива на 20%.

Рис.1.2.1 Изгибные колебания

Рис.1.2.2 Продольные колебания

Рис.1.2.3 Крутильные колебания