Список использованных источников. на тему: Теплопередача. Основные закономерности

РЕФЕРАТ

на тему: Теплопередача. Основные закономерности. Передача тепла теплопороводностью.

 

 

Выполнил: студент группы ПСКб-09П1

Невзоров А.С.

Приняла: д.т.н., проф.

Чулкова И.Л.

 

Омск – 2012

Содержание

1 ТЕПЛОВЫЕ ПРОЦЕССЫ И АППАРАТЫ....................................... 3

2 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕПЛООБМЕНА...... 3

3 ТЕПЛОПРОВОДНОСТЬ...................................................................... 5

3.1 Температурное поле. Уравнение теплопроводности................... 6

3.2 Стационарная теплопроводность через плоскую стенку.............. 8

3.3 Стационарная теплопроводность через цилиндрическую стенку 10

3.4 Стационарная теплопроводность через шаровую стенку.......... 13

Список использованных источников.................................................... 14

1 ТЕПЛОВЫЕ ПРОЦЕССЫ И АППАРАТЫ

Тепловыми называются процессы, скорость протекания которых определяется скоростью подвода или отвода теплоты.

В производстве искусственных строительных материалов тепловая обработка является важным переделом при изготовлении большинства видов изделий. Зачастую эта операция – конечная стадия технологической переработки, определяющая свойство строительного материала и качество получаемых изделий. Как правило, тепловая обработка осложняется массообменными процессами.

Отнесение процесса, происходящего в аппарате или установке, к тому или иному классу определяется целенаправленностью процесса. Например, во время сушки удаляется влага, т. е. происходит массообменный процесс. Однако характер его протекания, изменения параметров процесса и даже его скорость во многом определяется законами теплопередачи т. е. тепловыми процессами. Из наиболее распространенных тепловых процессов, как нагревание, охлаждение, конденсация и испарение, по существу, тепловыми являются только два первых, остальные же определяются не только законами переноса теплоты, но и законами массообмена.

 

2 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕПЛООБМЕНА

Теория теплообмена изучает процессы распространения теплоты в твердых, жидких и газообразных телах. Перенос теплоты может передаваться тремя способами:

· теплопроводностью;

· конвекцией;

· излучением (радиацией).

Процесс передачи теплоты теплопроводностью происходит при непосредственном контакте тел или частицами тел с различными температурами и представляет собой молекулярный процесс передачи теплоты. При нагревании тела, кинетическая энергия его молекул возрастает и частицы более нагретой части тела, сталкиваясь с соседними молекулами, сообщают им часть своей кинетической энергии.
Конвекция – это перенос теплоты при перемещении и перемешивании всей массы неравномерно нагретых жидкости или газа. При этом, перенос теплоты зависит от скорости движения жидкости или газа прямо пропорционально. Этот вид передачи теплоты сопровождается всегда теплопроводностью. Одновременный перенос теплоты конвекцией и теплопроводностью называется конвективным теплообменом.
В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей.
Процесс передачи теплоты внутренней энергии тела в виде электромагнитных волн называется излучением (радиацией). Этот процесс происходит в три стадии: превращение части внутренней энергии одного из тел в энергию электромагнитных волн, распространение э/м волн в пространстве, поглощение энергии излучения другим телом. Совместный теплообмен излучением и теплопроводностью называют радиационно-кондуктивным теплообменом.
Совокупность всех трех видов теплообмена называется сложным теплообменом.
Процессы теплообмена могут происходит в различных средах: чистых веществах и разных смесях, при изменении и без изменения агрегатного состояния рабочих сред и т.д. В зависимости от этого теплообмен протекает по разному и описывается различными уравнениями.

 

3 ТЕПЛОПРОВОДНОСТЬ

3.1 Температурное поле. Уравнение теплопроводности

Будем рассматривать только однородные и изотропные тела, т.е. такие тела, которые обладают одинаковыми физическими свойствами по всем направлениям. При передачи теплоты в твердом теле, температура тела будет изменяться по всему объему тела и во времени. Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем:

t = f(x,y,z,τ), (3.1)

где:t –температура тела;

x,y,z -координаты точки;

τ - время.
Такое температурное поле называется нестационарным ∂t/∂i ¹ 0, т.е. соответствует неустановившемуся тепловому режиму теплопроводности
Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным:

t = f(x,y,z), ∂t/∂i = 0 (3.2)

Уравнение двухмерного температурного поля:
для нестационарного режима:

t = f(x,y,τ); ∂t/∂z = 0 (3.3)

для стационарного режима:

t = f(x,y), ∂t/∂z = 0; ∂t/∂i = 0 (3.4)

Уравнение одномерного температурного поля:
для нестационарного режима:

t = f(x,τ); ∂t/∂y = ∂t/∂z = 0; ∂t/∂i ¹ 0 (3.5)

для стационарного режима:

t = f(x); ∂t/∂y = ∂t/∂z = 0; ∂t/∂i = 0 (3.6)

Изотермической поверхностью называется поверхность тела с одинаковыми температурой.
Рассмотрим две изотермические поверхности (Рис 3.1) с температурами t и t + ∆t. Градиентом температуры называют предел отношения изменения температуры∆tк расстоянию между изотермами по нормали ∆n, когда стремится к нулю:

gradt = | gradt | = lim[∆t/∆n]_∆n→0 = ∂t/∂n (3.7)

 

Рис. 3.1

Температурный градиент-это вектор, направленной по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры t по нормали n:

gradt = ∂t/∂n n_o, (9.7^*)

где: n_o – единичный вектор.

Количество теплоты, проходящее через изотермическую поверхность F в единицу времени называется тепловым потоком – Q, [Вт].
Тепловой поток, проходящий через единицу площади называют плотностью теплового потока – q = Q / F, [Вт/м²]
Для твердого тела уравнение теплопроводности подчиняется закону Фурье:
Тепловой поток, передаваемая теплопроводностью, пропорциональна градиенту температуры и площади сечения, перпендикулярного направлению теплового потока.

Q = -λ∙F∙ ∂t/∂n, (3.8)

или

q = -λ ∙ ∂t/∂n ∙ n_o = -λ∙ grad t, (3.9)

где: q – вектор плотности теплового потока;

λ – κоэффициент теплопроводности, [Вт/(м∙К)].
Численное значение вектора плотности теплового потока равна:

q = -λ∙ ∂t/∂n = -λ∙| gradt |, (3.10)

где: |gradt|- модуль вектора градиента температуры.
Коэффициент теплопроводности является физическим параметром вещества, характеризующим способность тела проводит теплоту. Она зависит от рода вещества, давления и температуры. Также на её величину влияет влажность вещества. Для большинства веществ коэффициент теплопроводности определяются опытным путем и для технических расчетов берут из справочной литературы.

Дифференциальное уравнение теплопроводности для трехмерного нестационарного температурного поля имеет следующий вид:

∂t/∂τ=a(d²t/dx²+d²t/dy²+d²t/dz²), (3.11)

где: а = λ/(ρ·ρ) – коэффициент температуропроводности [м²/с], характеризует скорость изменения температуры.

Для стационарной задачи, дифференциальное уравнение имеет вид:

a(d²t/dx²+d²t/dy²+d²t/dz²)=0, (3.12)

 

3.2 Стационарная теплопроводность через плоскую стенку

1).Однородная плоская стенка (Рис.3.2).

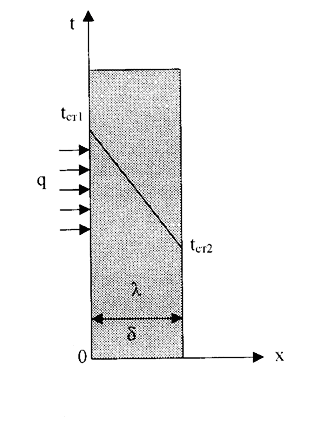
Рис. 3.2

Если R =δ/λ -термическое сопротивление теплопроводности стенки [(м²∙К)/Вт], то плотность теплового потока:

q = (t_ст1 – t_ст2)/R. (3.13)

Общее количество теплоты, которое передается через поверхность F за время τ определяется:

Q = q∙F∙τ = (t_ст1 – t_ст2)/R·F∙τ. (3.14)

Температура тела в точке с координатой х находится по формуле:

t_x = t_ст1 – (t_ст1 – t_ст2)∙x/ δ. (3.15)

2).Многослойная плоская стенка.
Рассмотрим 3-х слойную стенку (Рис.3.3). Температура наружных поверхностей стенокt_ст1 и t_ст2, коэффициенты теплопроводности слоевλ₁, λ₂, λ₃, толщина слоевδ₁, δ₂, δ₃.

Рис. 3.3
Плотности тепловых потокок через каждый слой стенки:

q = λ₁/δ₁∙(t_ст1 – t_сл1), (3.16)

q = λ₂/δ₂∙(t_сл1 – t_сл2), (3.17)

q = λ₃/δ₃∙(t_сл2 – t_ст2), (3.18)

Решая эти уравнения, относительно разности температур и складывая, получаем:

q = (t₁ – t₄)/(δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃) = (t_ст1 – t_ст4)/R_o , (3.19)

где: R_o = (δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃) – общее термическое сопротивление теплопроводности многослойной стенки.
Температура слоев определяется по следующим формулам:

t_сл1 = t_ст1 – q∙(δ₁/λ₁). (3.20)

t_сл2 = t_сл1 – q·δ₂/λ₂). (3.21)

3.3 Стационарная теплопроводность через цилиндрическую стенку

1). Однородная цилиндрическая стенка.
Рассмотрим однородный однослойный цилиндр длиной l, внутренним диаметром d₁и внешним диаметром d₂ (Рис.3.4).

Рис. 3.4

Температуры поверхностей стенки –t_ст1 и t_ст2.
Уравнение теплопроводности по закону Фурье в цилиндрических координатах:

Q = - λ∙2∙π∙r ·l· ∂t / ∂r, (3.22)

или

Q = 2·π·λ·l·Δt/ln(d₂/d₁), (3.23)

где: Δt = t_ст1 – t_ст2 – температурный напор;

λ – κоэффициент теплопроводности стенки.

Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут:

q_l = Q/l =2·π·λ·Δt /ln(d₂/d₁), [Вт/м]. (3.24)

Температура тела внутри стенки с координатойd_х:

t_x = t_ст1 – (t_ст1 – t_ст2) ·ln(d_x/d₁) / ln(d₂/d₁). (3.25)

2). Многослойная цилиндрическая стенка.

Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.3.5).

Рис. 3.5

Температура внутренней поверхности стенки –t_ст1, температура наружной поверхности стенки –t_ст2, коэффициенты теплопроводности слоев -λ₁, λ₂, λ₃, диаметры слоев d₁, d₂, d₃, d₄.
Тепловые потоки для слоев будут:

1-й слой: Q = 2·π· λ₁·l·(t_ст1 – t_сл1)/ ln(d₂/d₁), (3.26)

2-й слой: Q = 2·π·λ₂·l·(t_сл1 – t_сл2)/ ln(d₃/d₂), (3.27)

3-й слой: Q = 2·π·λ₃·l·(t_сл2 – t_ст2)/ ln(d₄/d₃), (3.28)

Решая полученные уравнения, получаем для теплового потока через многослойную стенку:

Q = 2·π·l·(t_ст1 – t_ст2) / [ln(d₂/d₁)/λ₁ + ln(d₃/d₂)/λ₂ + ln(d₄/d₃)/λ₃]. (3.29)

Для линейной плотности теплового потока имеем:

q_l = Q/l = 2·π· (t₁ – t₂) / [ln(d₂/d₁)/λ₁ + ln(d₃/d₂)/λ₂ + ln(d₄/d₃)/λ₃]. (3.30)

Температуру между слоями находим из следующих уравнений:

t_сл1 = t_ст1 – q_l·ln(d₂/d₁) / 2·π·λ₁ . (3.31)

t_сл2 = t_сл1 – q_l·ln(d₃/d₂) / 2·π·λ₂ . (3.32)

 

3.4 Стационарная теплопроводность через шаровую стенку

Пусть имеется полый шар (Рис.3.6) – внутренний диаметр d₁, внешний диаметрd₂, температура внутренней поверхности стенки –t_ст1, температура наружной поверхности стенки –t_ст2, коэффициент теплопроводности стенки -λ.

Рис. 3.6

Уравнение теплопроводности по закону Фурье в сферических координатах:

Q =4·π·λ·Δt/(1/r₂ - 1/r₁) =2·π·λ·Δt/(1/d₁ - 1/d₂) =
= 2·π·λ·d₁·d₂·Δt /(d₂ - d₁) = π·λ·d₁·d₂·Δt / δ, (3.33)

где: Δt = t_ст1 – t_ст2 – температурный напор;

δ –толщина стенки.

Список использованных источников

1. Лариков Н.Н. Теплотехника: Учебник для вузов. -3-е изд., перераб. и дополн.-М.; Стройиздат, 1985 -432 с.ил.

2. Борщ И.М. Процессы и аппараты в технологии строительных материалов. -Киев.; Вища школа, 1981 -296с.

3. Луканин В.Н., Шатров М.Г., Камфер Г.М. и др. Теплотехника: Учебник для вузов. –М.; Высш.шк., 1999.-671 с.ил.

4. Тихомиров К.В. Теплотехника, теплоснабжение и вентиляция. -М.; Стройиздат, 1981-248с.