Практическая работа №1
Тема: Определение опорных реакций
Цель работы: научиться находить реакции опорных устройств балочных систем.
Краткие теоретические сведения
Общие сведения
Часто в машинах и конструкциях используют тела удлинённой формы, называемые балками. Они предназначены для восприятия поперечных нагрузок и имеют специальные опорные устройства (описанные ниже), предназначенные для их сопряжения с другими элементами.
Три формы уравнения равновесия произвольной плоской системы сходящихся сил
- 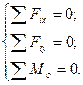 (1)
(1)
где  - сумма проекций всех сил на ось х,
- сумма проекций всех сил на ось х,
 - сумма проекций всех сил на ось у;
- сумма проекций всех сил на ось у;
 - сумма моментов относительно произвольной точки О.
- сумма моментов относительно произвольной точки О.
-  (2)
(2)
где  ,
,  ,
,  - суммы моментов относительно трёх произвольно лежащих точек, не лежащих на одной прямой.
- суммы моментов относительно трёх произвольно лежащих точек, не лежащих на одной прямой.
-  (3)
(3)
где  ,
,  , - суммы моментов относительно двух произвольно лежащих точек;
, - суммы моментов относительно двух произвольно лежащих точек;
 - сумма проекций сил на некоторую ось, не перпендикулярную прямой, проходящей через точки А и В.
- сумма проекций сил на некоторую ось, не перпендикулярную прямой, проходящей через точки А и В.
Опорные устройства балочных систем
- шарнирно – подвижная опора. Эта опора допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. В данной опоре известны точка приложения опорной реакции – центр шарнира и её направление – перпендикуляр к опорной плоскости. Следовательно, неизвестным является лишь значение опорной реакции  . Вид графического представления данной опоры представлен на рисунке 1:
. Вид графического представления данной опоры представлен на рисунке 1:

Рисунок 1 – Графическое изображение шарнирно-подвижной опоры
- шарнирно – неподвижная опора – данная опора допускает лишь поворот вокруг оси шарнира, без линейных перемещений. Является неизвестным направление и значение опорной реакции, которую принято раскладывать на две составляющие:  . Вид графического представления данной опоры представлен на рисунке 2:
. Вид графического представления данной опоры представлен на рисунке 2:

Рисунок 2 – Графическое изображение шарнирно-неподвижной опоры
- жёсткая заделка – данная опора не допускает ни линейных перемещений, ни поворота. Для определения опорной реакции необходимо найти три неизвестные: составляющие  и реактивный момент Ма. Вид графического представления данной опоры представлен на рисунке 3:
и реактивный момент Ма. Вид графического представления данной опоры представлен на рисунке 3:

Рисунок 3 – Графическое изображение жёсткой заделки
Рекомендации по решению задания
Целесообразно составлять уравнения так, чтобы они могли быть решены наиболее просто и быстро. Быстро решается система уравнений равновесия, каждое из которых содержит одну из неизвестных. К такой системе можно перейти, корректно выбирая направления координатных осей и задавая точку центра моментов.
В качестве центра моментов рекомендуется выбирать точку пересечения двух неизвестных сил, направление координатных осей – так, чтобы оси были перпендикулярны неизвестным силам.
Рекомендуется во избежание накопления ошибок при округлении все результаты промежуточных вычислений записывать с точностью до трёх знаков после запятой.
2. Пример расчёта
Пусть имеется балка, крепимая с помощью шарнирно-подвижной и шарнирно-неподвижной основ, изображённая на рисунке 4:

Рисунок 4 – Условие задачи
На эту балку действуют две распределённые силы с интенсивностями: q1 = 5Н и q2 = 10Н, сила F = 15Н и пара сил, создающая момент М = 20Н*м. Длинна балки составляет 1,7м. Определить опорные реакции балки.
Решение:
1). Освобождаем балку от опор и заменяем их действие реакциями (в соотв. с п.1) Ra, Rdx, Rdy. (Указание: В случае жёсткой заделки не забывайте изобразить момент её пары сил!). Выбираем и указываем на рисунке 5 направления координатных осей так, чтобы оси были перпендикулярны некоторым неизвестным силам:

Рисунок 5 – Вид балки после замены опор реакциями
2). Заменяем распределённые нагрузки их равнодействующими и изображаем их на рисунке 6:

Рисунок 6 – Вид балки после замены распределённых нагрузок равнодействующими
3). Составляем уравнения равновесия (Указание: используйте любую из трёх представленных в пункте 1 форм условий равновесия). Составим уравнения равновесия для первой формы:
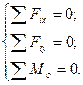 (4)
(4)
Данные уравнения для нашей балки будут записаны, как:
 (5)
(5)
Решим эту систему и найдём реакции опор:
 ; (6)
; (6)

 (7)
(7)

Отрицательное значение в выражении для 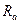 показывает, что на графике надо изменить направление действия этой реакции на противоположное.
показывает, что на графике надо изменить направление действия этой реакции на противоположное.
4). Производим проверку полученного результата, а именно – посчитаем уравнение равновесия для точки Е балки:
 (8)
(8)


 ; (9)
; (9)
Условие равновесия выполнено, следовательно расчёт произведён верно. Ответ: Ra = 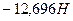 ; Rdx = 0; Rdy =
; Rdx = 0; Rdy =  .
.
Задание к работе
Работа выполняется по индивидуальному заданию – карточке, выдаваемому преподавателем.
4. Содержание отчёта
1. Тема и цель работы.
2. Рисунок с заданием.
3. Исходные данные, сгруппированные в таблицу 1:
Таблица 1 – Вид представления в отчёте исходных данных к работе.

4. Решение задачи по нахождению опорных реакций.
5. Проверка полученного значения.
6. Ответ.
7. Вывод: анализ полученных данных.






