В программе «Дифракция» предлагается серия компьютерных экспериментов, моделирующих опыты по дифракции света на препятствиях различной формы при различных условиях наблюдения. На рис.7,8 показаны виды экранов, используемых в данной программе, и даны пояснения к каждому пункту меню. Программа разделена на три части, указанные в основном меню:
1. Распределение интенсивности (дифракционные явления при различных значениях волнового параметра).
2. Дифракция Френеля.
3. Дифракция Фраунгофера.
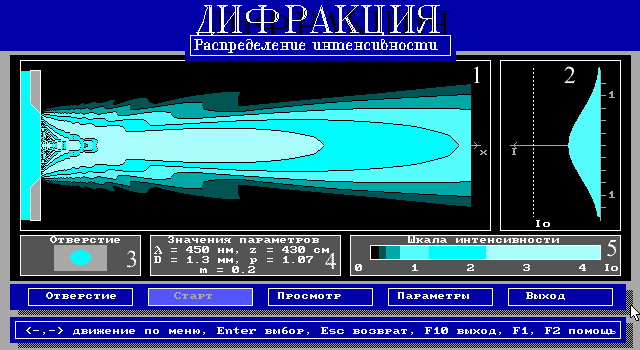
В первой части программы (рис.7) компьютер на основе вычисления интегралов Френеля–Кирхгофа строит в динамическом режиме продольный разрез дифракционного поля при дифракции света на щели и на круглом отверстии. В окне 1 показана общая структура дифракционного поля на различных расстояниях плоскости наблюдения от препятствия. Результаты расчета выводятся на экран в виде картины, на которой области с различным значением интенсивности изображены либо различными цветами, либо оттенками одного цвета. В окне 2 показано распределение интенсивности света в выбранной плоскости наблюдения. В окне 3 изображена геометрическая форма препятствия (щель, круглое отверстие). Окно 4 – окно параметров, окно 5 – шкала интенсивности.
|
| Рис.7. Распределение интенсивности в дифракционной картине. |
1 – структура дифракционного поля; 2 – график интенсивности в текущем разрезе дифракционного поля; 3 – форма отверстия; 4 – окно параметров; 5 – шкала интенсивности.

а) выбор формы отверстия; b) начало компьютерного эксперимента; с) просмотр дифракционного поля; d) изменение параметров и типа шкалы.
В окне 4 выводится текущее значение волнового параметра p, изменяющееся по мере удаления плоскости наблюдения от экрана, m – число зон Френеля, а также длина волны λ и размер препятствия D. Параметры λ, D, z – расстояние плоскости наблюдения от экрана, могут изменяться по желанию пользователя, причем диапазон изменений этих параметров соответствует физическим условиям реальных оптических опытов. Следует обратить особое внимание на изменение качественной структуры дифракционного поля при изменении условий эксперимента. Продольное сечение дифракционного поля, воссоздающееся на экране, позволяет визуально выделить область геометрической оптики, область дифракции Френеля (ближняя волновая зона) и область дифракции Фраунгофера (дальняя волновая зона).
Следует отметить, что адекватное изображение разреза дифракционного поля является непростой задачей для компьютерной графики. Для большего удобства в программе предусмотрено изображение результатов расчета дифракционного поля разными способами (пункт меню «Картинка»). Сечение дифракционного поля изображается в виде своеобразной «томограммы» (пункт меню «Томограмма»), где области с различными уровнями интенсивности изображаются различными цветами или оттенками одного цвета; при этом границы этих областей четко очерчены и поэтому удобно наблюдать основные максимумы в дифракционной картине. Однако, такая томограмма, разумеется, мало похожа на реально наблюдаемую картину дифракции. При использовании одного цвета и непрерывной шкалы интенсивностей (пункт меню «Непрерывно») изображение дифракционного поля в большей степени напоминает реальный эксперимент. Однако, при этом в областях малой интенсивности возможно появление отдельных точек, что следует рассматривать как погрешности графики. В программе предлагается также картинка, построенная в логарифмическом масштабе интенсивности (пункт меню «Логарифм»).
Вторая часть программы посвящена изучению дифракционных явлений в ближней волновой зоне (дифракция Френеля). Методом векторных диаграмм и зон Френеля рассмотрены задачи дифракции света на круглом отверстии, щели и крае экрана. На рис.8 в окне 1 показана схема дифракционного эксперимента, в окне 2 – имитация визуально наблюдаемой дифракционной картины, в окне 3 – распределение интенсивности в дифракционной картине. Окно 4 – предназначено для схематического изображения экрана и границ зон Френеля. В окне 5 выводится информация о параметрах эксперимента; в окне 6 изображена векторная диаграмма (векторная диаграмма для кольцевых зон Френеля при дифракции света на круглом отверстии и спираль Корню при дифракции света на щели, или на краю экрана). В окне параметров указывается число m открытых зон Френеля и значение волнового параметра p. В программе предусмотрена возможность изменения параметров λ и z. Для случая дифракции на краю экрана программа иллюстрирует применение спирали Корню к расчету дифракционной картины при поперечном смещении точки наблюдения.
В третьей части изучается дифракция Фраунгофера на щели и круглом отверстии. Окна на экране расположены аналогично рис.8. В компьютерном эксперименте изучается дифракционная картина в фокальной плоскости линзы.

|
| Рис.8. Дифракция Френеля. |
1 – схема эксперимента; 2 – дифракционная картина; 3 – график распределения интенсивности; 4 – информация о параметрах эксперимента; 5 – изображение отверстия и границ зон Френеля; 6 – векторные диаграммы.

а) выбор формы отверстия; b) изменение А; с) изменение расстояния до экрана; d) изменение размера отверстия.
Задание к работе в лаборатории.
1) Используя два типа входных отверстий (круглое, щелевое) рассмотреть распределение интенсивности в пространстве в зависимости от различных длин волн и диаметров входного отверстия.
2) На примере одного из отверстий рассмотреть дифракцию Френеля.
3) На примере двух отверстий (круглого и щелевого) рассмотреть дифракцию Фраунгофера.






