Лабораторная работа № 3
«Аттестация методики выполнения измерения»
Выполнил: Ст. 41(1) ПГ Белячков А.В.
Проверил: Кузнецов А.И.
Москва,2012
Задание: произвести аттестацию методики определения смещения деформационных марок с заданной точностью 
. С этой целью были выполнены опытные измерения смещений деформационных марок, расположенных через расстояние D вдоль створа, задаваемого опорными пунктами. При этом теодолит располагался на одной стороне створа (односторонние измерения) и положение каждой марки определялось 10-ю приемами (рис.1).
Исходные данные:
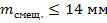– СКП определения смещения;
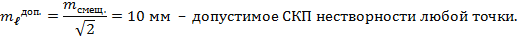
Для наблюдения за изменением тела оползня заложены 6 марок. Расстояние между марками D=60 метров. Характеристика нестворности данных марок приведены в табл. 1
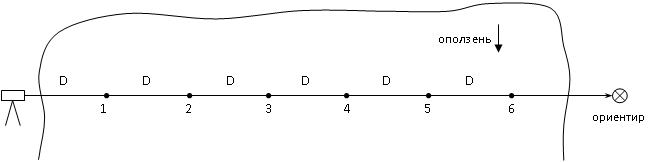
Рис.1. Схема выполняемых измерений
Характеристика нестворности марок
Табл. 1
| Нестворности | ||||||
| № | 1 D | 2 D | 3 D | 4 D | 5 D | 6 D |
| Ср. (l)знач | 279,8 | 309,7 | 256,2 | 171,1 | 305,4 |
Решение:
Вычислим отклонение от среднего каждого цикла наблюдений и оценим их точность по формулеБесселя: 
См. Табл.2
Отклонение каждого цикла наблюдений от среднего и определение СКП наблюдений.
Табл. 2
| № | 1 D (v) | 2 D (v) | 3 D (v) | 4 D (v) | 5 D (v) | 6 D (v) |
| -0,8 | -2 | 4,3 | -6,2 | 6,9 | 10,6 | |
| 1,2 | -3,7 | 5,8 | 5,9 | -1,4 | ||
| -1,8 | -3 | -2,7 | 1,8 | -7,1 | -13,4 | |
| -1,8 | -3,7 | -4,2 | -6,1 | -8,4 | ||
| 2,2 | 6,3 | -4,2 | 7,9 | 11,6 | ||
| 2,2 | 1,3 | 3,8 | -0,1 | 10,6 | ||
| 0,2 | -3 | 0,3 | 4,8 | -3,1 | -15,4 | |
| -0,8 | 4,3 | 1,8 | 6,9 | 5,6 | ||
| -0,8 | -3,7 | -2,2 | -6,1 | -10,4 | ||
| 0,2 | -2 | -2,7 | -1,2 | -5,1 | 10,6 | |
(Sl)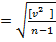 
| 1,37 | 2,28 | 3,77 | 4,08 | 6,16 | 11,06 |
Сравнить полученные значенияSlс допустимым значением Slдоп = 10мм.
Необходимо создать модель, отражающую зависимость погрешности от расстояния между прибором и маркой (т.е. вывести уравнение регрессии). Форму модели выбрать между линейной и квадратичной зависимостями, качество которых оценить по отклонениям реальных и статистических значений.
В нашем случае разброс данных для наиболее удаленной марки превышает допустимое значение, поэтому на данном этапе нельзя признать методику аттестованной, и необходимо перейти к следующему этапу решения.
Квадратичная регрессия
| Вычисление коэффициентов квадратичного уравнения регрессии. | |||||||
| n | D | D^2 | D^3 | D^4 | Sl | Sl*D | Sl*D^2 |
| 1,4 | 82,2 | 4933,2 | |||||
| 2,3 | 273,9 | 32872,1 | |||||
| 3,8 | 677,8 | 121997,0 | |||||
| 4,1 | 980,1 | 235229,4 | |||||
| 6,2 | 1848,2 | 554472,7 | |||||
| 11,1 | 3980,7 | 1433042,4 | |||||
| 28,7 | 7843,0 | 2382546,8 |
1) Составим уравнения регрессии, показывающее зависимость 
от D:
Квадратичная регрессия (считается наиболее надежной).
Выражается уравнением вида:
Коэффициенты a, b, c определяются из решения системы уравнений
| |||||||||
| D, м | ||||||
| Sl, мм | 1,8 | 1,9 | 2,9 | 4,6 | 7,1 | 10,4 |
Максимально допустимая СКП нестворности равна 10 мм
Линейная регрессия
2)Составим уравнения регрессии, показывающее зависимость от D:
| Коэффициенты | a | 0,028854 | |
| линейного | b | 1,344737 | |
| ур-я регрессии | |||
Оценка точности уравнения регрессии:
| Квадратичного уравнения регрессии. |
| Sli | Slэмп. | Sli - Slэмп. | (Sli - Slэмп.)^2 |
| 1,37 | 1,80 | -0,43 | 0,19 |
| 2,28 | 1,93 | 0,35 | 0,12 |
| 3,77 | 2,86 | 0,90 | 0,82 |
| 4,08 | 4,59 | -0,50 | 0,25 |
| 6,16 | 7,11 | -0,95 | 0,90 |
| 11,06 | 10,43 | 0,63 | 0,40 |
| Ʃ | 2,67 | ||
| Ss | 0,82 |
Где Ss- надежность СКП
Оценка точности линейных коэффициентов регрессии
| Sli | Slэмп. | Sli - Slэмп. | (Sli - Slэмп.)^2 |
| 1,37 | 0,60 | 0,77 | 0,59 |
| 2,28 | 2,00 | 0,28 | 0,08 |
| 3,77 | 3,90 | -0,13 | 0,02 |
| 4,08 | 5,80 | -1,72 | 2,95 |
| 6,16 | 7,70 | -1,54 | 2,37 |
| 11,06 | 9,30 | 1,76 | 3,089 |
| Ʃ | 9,09 | ||
| Ss | 1,51 |
Из оценки уравнений регрессии мы видим что,Ss - надежность квадратичной регрессия является более точной в 0,5 раза, чем надёжность линейной регрессии (Ssквадр.=0,82, а Ssлин=1,51)поэтому мы будем использовать её.
Максимальное расстояние до марки:
= 353м при ml=10 мм
Вывод: На основании проведенных результатов математической обработки в программе Exel построены соответствующие графики (линейной и квадратичной регрессии). Произведена оценка уравнений регрессии. По этим данным делаем вывод, что аттестация производится по уравнению квадратичной регрессии.
Аттестация методики измерения оползня можно применить при максимальном расстоянии до деформационной марки 353м. Погрешность нестворности конечной точки составляет 10,4 мм, что превышает допуск в 10 мм. Данную технологию измерения нельзя аттестовать.
Оценка точности уравнениярегрессии:
Где Sℓ эмп- надежность СКП
Оценка точности линейных коэффициентов регрессии
Из оценки уравнений регрессии мы видим что квадратическая регрессия является более надежной, поэтому мы будем использовать ее. максимальное расстояние до марки:
|
= 353м при ml=10 ммМетрологическая оценка метода
| Найдём Sv, принимая соответственно Т = 1 год, 0,5 года, 0,25 года а Sl = 10 мм | ||||||
| DT, год | Sv, мм/год | V мм/год | ||||
| 0,5 | ||||||
| 0,25 |
Вывод:Погрешность нестворности конечной точки составляет составляет 10,4 мм, что превышает допуск в 10 мм.Данную технологию измерения оползня нельзя аттестовать.
