Массивы
Массив состоит из нескольких элементов одного и того же типа. Можно выбирать любой элемент массива. Для этого необходимо задать индекс, который указывает относительную позицию элемента в массиве. Число элементов массива задается при его объявлении и в дальнейшем не меняется. Если массив объявлен, к любому его элементу можно обратиться следующим образом: указать имя массива и индекс его элемента в квадратных скобках.
Массивы объявляются так же, как и переменные. Например:
int a[100];
float c[10][20];
В первой строке объявляем массив а из 100 элементов целого типа: а[0],a[1], …,a[99] (индексация всегда начинается с нуля). Во второй строке объявлен двумерный массив вещественного типа. Двумерный массив представляется как одномерный, элементы которого являются тоже массивами. В первых квадратных скобках указывается количество строк в массиве, во вторых – количество столбцов.
Массив можно инициализировать, т.е. присвоить его элементам начальные значения. Это делается при объявлении типа массива, например: int a[5]= { 0, 0, 0, 0, 0};
Это значит, что все элементы массива получают нулевое значение.
При инициализации число элементов можно не указывать, т.к. в этом случае оно может быть вычислено по количеству присваиваемых значений (в фигурных скобках), например:
int a[] = {10,20,30,40,50};
Двумерный массив можно инициализировать следующим образом:
int a[][3] = {
{10,20,30},
{40,50,60},
{70,80,90}
};
Первая размерность массива будет определена автоматически.
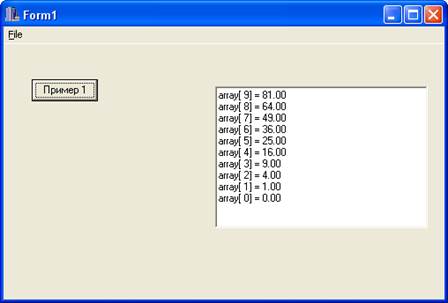
Пример 1. Работа с одномерным массивом
Требуется создать одномерный массив, состоящий из десяти элементов вещественного типа. Требуется инициализировать и вывести на экран значения элементов этого массива в обратном порядке.
void __fastcall TForm1::Button1Click(TObject *Sender)
{
float array [10];
int i;
String S;
for (i=0;i<10;i++)
array[i] = i*i;
for (i=9;i > -1;i --)
{
S.sprintf ("array[%2d] = %4.2f", i, array[i]);
Memo1->Lines->Add(S);
}
}
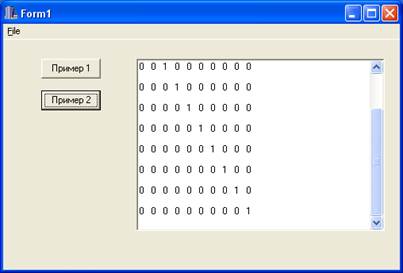
Пример 2. Создаем и выводим на экран единичную матрицу
Квадратная матрица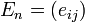 
размера (порядка 
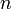), где 
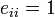для всякого 
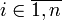, и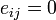 
для всяких 
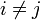, называется единичной матрицей порядка 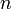. Единичная матрица размера 
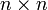обычно обозначается 
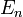и имеет вид:
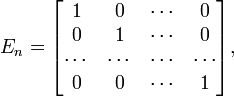
Так же используется и другое обозначение: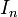 
.
Свойства
- Произведение любой матрицы и единичной матрицы подходящего размера равно самой матрице:
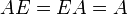
- Квадратная матрица в нулевой степени дает единичную матрицу того же размера:
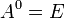
- При умножении матрицы на её обратную матрицу получается единичная матрица:
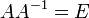
- Единичная матрица получается при умножении ортогональной матрицы на ей транспонированную:
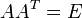
- Определитель единичной матрицы равен единице:
.
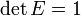void __fastcall TForm1::Button2Click(TObject *Sender)
{
float E[10][10];
int i, j;
String S;
for (i=0;i<10;i++)
for (j=0;j<10;j++)
if (i == j) E[i][j] =1.0;
else E[i][j] =0.0;
// вывод на экран
for (i=0;i<10;i++)
{
S.sprintf ("");
Memo1->Lines->Add(S);
for (j=0;j<10;j++)
S.cat_sprintf("%1.0f ",E[i][j]);
Memo1->Lines->Add(S);
}
return;
}
Пример 3. Вычисление следа матрицы.
След м а трицы – это сумма диагональных элементов матрицы. Это понятие устанавливается только для квадратной матрицы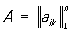 
След матрицы обозначается через Sp A (от нем. Spur — след) или Тr А (от англ. tract — след).
Таким образом: Sp А = a11+ a22 +... + ann.
void __fastcall TForm1::Button3Click(TObject *Sender)
{
float Tr = 0.0,A[][5]={
{1,2,3,4,5},
{6,7,8,9,5},
{5,6,7,8,9},
{2,3,5,6,5},
{1,2,3,4,5}
};
String S;
for (int i =0; i < 5; i++)
Tr = Tr + A[i][i];
S.sprintf ("Tr A= %4.2f", Tr);
Label1->Caption=S;
return;
}
