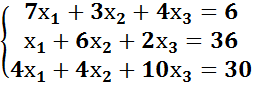СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1.РЕШЕНИЕ СЛАУ МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ
1.1 Описание метода решения
1.2 Исходные данные
1.3 Алгоритм
1.4 Программа на языке QBasic
1.5 Результат работы программы
1.6 Проверка результата работы программы
2. УТОЧНЕНИЕ КОРНЯ МЕТОДОМ КАСАТЕЛЬНЫХ
2.1 Описание метода решения
2.2 Исходные данные
2.3 Алгоритм
2.4 Программа на языке QBasic
2.5 Результат работы программы
2.6 Проверка результата работы программы
3.ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ПО ПРАВИЛУ ПРЯМОУГОЛЬНИКА
3.1 Описание метода решения
3.2 Исходные данные
3.3 Алгоритм
3.4 Программа на языке QBasic
3.5 Проверка результата работы программы
4.WinRAR
4.1 Общие сведения о программе
4.1.1 Назначение и отличительные особенности
4.1.2 Ограничения WinRAR
4.1.3 Системные требования WinRAR
4.2 Интерфейс WinRAR
4.3 Режимы управления файлами и архивами
4.4 Использование контекстных меню
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Целью данной курсовой работы является разработка алгоритмов и программ для решения системы линейных алгебраических уравнений с помощью метода Гаусса; нелинейного уравнения с помощью метода хорд; для численного интегрирования по правилу трапеций.
Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.
Способы решения систем линейных алгебраических уравнений делятся на две группы:
· точные методы, представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, правило Крамера, метод Гаусса и др.),
· итерационные методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации, метод Зейделя и др.).
Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода.
Решение систем линейных алгебраических уравнений – одна из основных задач вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности – нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма.
Для того чтобы система линейных алгебраических уравнений имела решение, необходимо и достаточно, чтобы ранг основной матрицы был равен рангу расширенной матрицы. Если ранг основной матрицы равен рангу расширенной матрицы и равен числу неизвестных, то система имеет единственное решение. Если ранг основной матрицы равен рангу расширенной матрицы, но меньший числа неизвестных, то система имеет бесконечное число решений.
Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Этот метод известен в различных вариантах уже более 2000 лет. Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Строго говоря, описываемый выше метод правильно называть методом "Гаусса-Жордана" (Gauss-Jordan elimination), поскольку он является вариацией метода Гаусса, описанной геодезистом Вильгельмом Жорданом в 1887 г.). Также интересно заметить, что одновременно с Жорданом (а по некоторым данным даже раньше него) этот алгоритм придумал Класен (B.-I. Clasen).
Под нелинейными уравнениями понимаются алгебраические и трансцендентные уравнения вида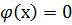 
, где х - действительное число, а 
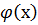– нелинейная функция. Для решения этих уравнений применяется метод хорд – итерационный численный метод приближенного нахождения корней. Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Кроме того, в некоторых случаях уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнения теряет смысл. Для их решения используются итерационные методы с заданной степенью точности. Решить уравнение итерационным методом значит установить, имеет ли оно корни, сколько корней и найти значения корней с нужной точностью.
Задача нахождения корня уравнения f(x) = 0 итерационным методом состоит из двух этапов:
· отделение корней - отыскание приближенного значения корня или содержащего его отрезка;
· уточнение приближенных корней - доведение их до заданной степени точности.
Определенным интегралом функции f(x), взятом в интервале от a до b, называется предел, к которому стремится интегральная сумма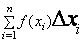 
при стремлении всех промежутков ∆xi к нулю. Согласно правилу трапеций, необходимо заменить график функции F(x) прямой, проходящей через две точки (х0,у0) и (х0+h,у1), и вычислить значение элемента интегральной суммы как площадь трапеции: 
.
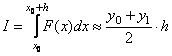РЕШЕНИЕ СЛАУ МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ
1.1 Описание метода постой итерации
Системы алгебраических уравнений (СЛАУ) имеют вид:
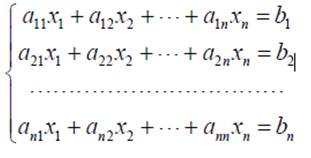
или, при записи в матричной форме:
A⋅ x = b,
В практике используют два типа методов численного решения СЛАУ – прямые и косвенные. При использовании прямых методов СЛАУ приводится к одной из специальных форм (диагональной, треугольной) позволяющих точно получить искомое решение (если таковое существует). Наиболее распространенным прямым методом решения СЛАУ является метод Гаусса. Итерационные методы служат для поиска приближенного решения СЛАУ с заданной точностью. Следует отметить, что итерационный процесс не всегда сходится к решению системы, а только тогда, когда последовательность получаемых при расчетах приближений стремиться к точному решению. При решении СЛАУ методом простой итерации ее преобразуют к виду, когда в левой части находится только одна из искомых переменных:
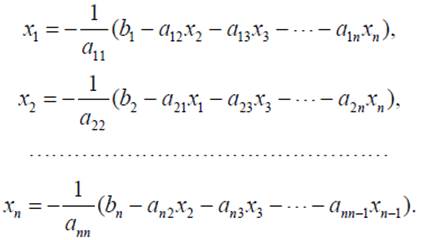
Задав некоторые исходные приближения xi, i=1,2,…,n, подставляют их в правую часть выражений и вычисляют новые значения x. Процесс повторяют до тех пор, пока максимальная из невязок, определяемых по выражению:
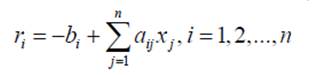
не станет меньше заданной точности ε. Если максимальная невязка при k -ой итерации окажется больше максимальной невязки при k-1 -ой итерации, то процесс аварийно завершают, т.к. итерационный процесс расходится. Для минимизации количества итераций новые значения x можно вычислять с использованием значением невязок на предыдущей итерации:
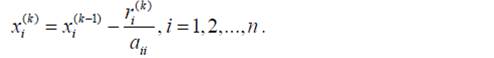
Невязки, в этом случае определяют по выражению:
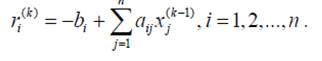
1.2 Исходные данные
В качестве исходных данных дана следующая СЛАУ:
