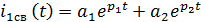
Общее решение: 
t)
Для нахождения i1(t) – тока в конденсаторе, определим UC(t)
Запишем систему уравнений для напряжения на конденсаторе:
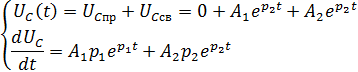
6) Определяем А1 и А2 из расчета системы при t=0 (начало переходного процесса)
По законам коммутации запишем независимые начальные условия:
Определим зависимые начальные условия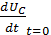 
из формулы
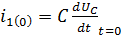
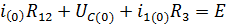
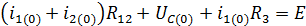
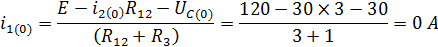
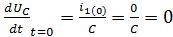
Подставляем значения в уравнение:
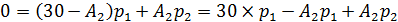
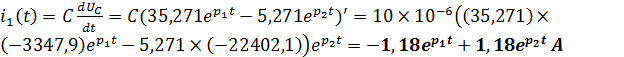
РАСЧЕТ ПЕРЕХОДНОГО ПРОЦЕССА ОПЕРАТОРНЫМ МЕТОДОМ
Суть операторного метода заключается в замене дифференциально-интегральных уравнений с вещественной переменной 
, алгебраическими уравнениями с некоторой комплексной переменной 
. Такая замена осуществляется за счет перевода решения из плоскости с переменной в плоскость с переменной .
Функции с вещественной переменной называются оригинальными.
Функции с комплексной переменной называются изображениями.
,
где 
- знак соответствия.
Для перехода от оригинала по найденному изображению используется прямое преобразование Лапласа:
Для определения оригинала по найденному изображению используют либо таблицы соответствия, либо формулу разложения.
,
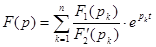где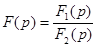 
, 
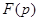-изображение искомой функции.
Составим операторную схему замещения:
Рассмотрим схему методом контурных токов. Найдем I1(p)=I11(p).
-квадратное уравнение такое же как в классическом методе
Приравниваем 
Получаем корни 
Производная: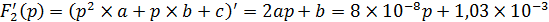 
По формуле разложения перейдем от I1(p) к i1(t):
Построим график закона изменения 
(t)
Задача №2
Дана Электрическая схема, на входе которой действует напряжение, изменяющейся во времени по заданному закону u1(t). Требуется определить закон изменения во времени тока в одной из ветви схемы или напряжения на заданном участке схемы. Параметры цепи R,L,C заданы в буквенном виде.
Задачу требуется решить с помощью интеграла Дюамеля. Искомую величину следует определить (записать ее аналитическое выражение) для всех интервалов времени. В зависимости от условий задачи полный ответ будет содержать два или три соотношения, каждое из которых справедливо лишь в определенном диапазоне времени.
В каждом ответе следует выполнить приведение подобных членов относительно 
и выделить постоянную составляющую.
Определить 
Формула интеграла Дюамеля:
Определим g(t)-переходную проводимость из расчета включения схемы на ЭДС E=1 В
Принужденное значение:
Свободная составляющая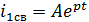 
Определим p-показатель затухания переходного процесса из расчета характеристического уравнения схемы:
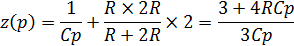
z(p)=0 если числитель 3+4RCp=0
Определим A-постоянную интегрирования из расчета схемы при t=0
По 2 закону коммутации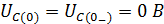 
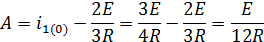
-g(t)-переходная проводимость
1) Запишем интеграл Дюамеля для 
На этом интервале: 
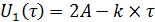
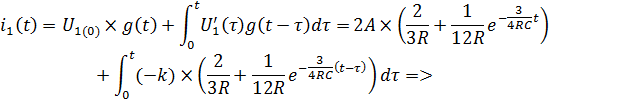
Заменим для удобства 
на p
=> 
2) Запишем интеграл Дюамеля для 
На этом интервале: 
Заменим на p
 |  |
3) Запишем интеграл Дюамеля для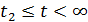 
На этом интервале: 
Заменим на p
«Нелинейные магнитные цепи постоянного тока»
Задача №3
1. Рассчитать магнитную цепь методом двух узлов и определить заданные величины.
2. Для принятых в п. 1 положительных направлений магнитных потоков и заданного направления МДС составить систему уравнений по законам Кирхгофа.
Указания: 1. Обозначения: l- длина средней магнитной линии одной ветви магнитной цепи;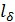 
- длина воздушного зазора (его положение в магнитной цепи дано на схемах магнитопроводов); S- сечение участков магнитопровода; ω-число витков катушек; I -постоянный ток в катушке.
Обозначения величин даются с индексами, которые указывают, к какой ветви магнитной цепи относится та или иная величина; индекс 1-к левой магнитной ветви, 2-к средней, 3-к правой.
2.Магнитные свойства стали, из которой изготовлены магнитопроводы, определяются кривой намагничивания, которая дана в следующей таблице:
| H, A/м | ||||||||||
| B, Тл | 0,22 | 0,75 | 0,93 | 1,02 | 1,14 | 1,28 | 1,47 | 1,53 | 1,57 | 1,6 |
Схема замещения магнитной цепи.
Дано:
e1=33,5 см=0,335 м e3=45 см=0,45 м
S1=7,6 см2=7,6×10-4 м2 S3=11,3 см2=11,3×10-4 м2
ω1=500 ω3=975
I1=0,21 A ω4=20
e2=12 см=0,12 м I4=0,5 A
S2=12 см2=12×10-4 м2 Ф3-Ф1=20×10-5 Вб
ω2=400
I2=0,05 A
Найти: I3 и Ф1
Составим уравнения по законам Кирхгофа для магнитных цепей:
(1)- по первому закону Кирхгофа
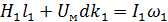
(2)-по второму закону Кирхгофа через Uмdk
Отсюда получаем:
(2.3)
I3 – неизвестно
Магнитные потоки в ветвях схемы рассчитаем по формулам:
Магнитные напряжения определим по формулам (2.1), (2.2)
Значения магнитной индукции B и напряженности магнитного поля H берем из заданной по условию кривой намагничивания: B=f(H)
Расчетная таблица
| Н, А/м | В, Тл |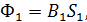 
10 Вб
| 
А
| 
10 Вб
| 
 ,
А
|
| 105.000 | 30.000 | ||||
| 0.22 | 1.672 | 98.300 | 2.640 | 27.600 | |
| 0.75 | 5.700 | 91.600 | 9.000 | 25.200 | |
| 1.02 | 7.752 | 78.200 | 12.240 | 20.400 | |
| 1.14 | 8.664 | 64.800 | 13.680 | 15.600 | |
| 1.28 | 9.728 | 38.000 | 15.360 | 6.000 | |
| 1.47 | 11.172 | -29.000 | 17.640 | -18.000 | |
| 1.53 | 11.628 | -96.000 | 18.360 | -42.000 | |
| 1.57 | 11.932 | -163.000 | 18.840 | -66.000 | |
| 1.6 | 12.160 | -297.000 | 19.200 | -114.000 |
По расчетным значениям построим графики 
, 
выразим из дополнительного условия Ф3
и подставим Ф3 в (1)
(3)
По графику находим точку “A”, где выполняется условие (3), перпендикуляром на ось Uмdk определяем Uмdkистинное=25 A и находим на этом Uмdkист магнитные потоки
Проверка по первому закону Кирхгофа:
 |
Ф,×10-4 Вб
20
Ф2
 |
15
 |
10,2
10 
Ф1
5
 |
Uмdk
-300 -200 -100 0 30 100 200 A
Uмdk=25 A
Магнитная индукция в третьем стержне:
По заданной кривой намагничивания B=f(H) определяем напряженность магнитного поля H3.
В, Тл
 |
1,8
1,6
1,4
1,2
1
0,8
0,6
0,4
0,2
0 Н, А/м
100 200 300 400 500 600 700 800 900 1000 1100 1200
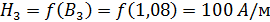
Из уравнения (2.3) выразим I3:
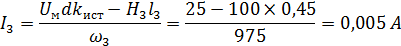
Проверка:
По кривой намагничивания:
Подставим найденные значения в уравнение (1):
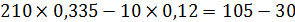
Задача №4
Рассчитать периодические процессы в нелинейной электрической цепи по характеристикам для мгновенных значений и построить графики изменения требуемых величин во времени.
Соответствуя своему варианту №84, решаю задачу 3д.
Схема рисунка 4.25 имеет резисторы сопротивлениями R1, R2, два идеальных диода, вольт-амперные характеристики которых изображены на рисунке 4.21, а, два источника синусоидальной ЭДС: 
и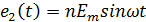 
(где n- численный коэффициент) и источник постоянной ЭДС Е0. Значения Еm, Е0, R1, R2 и n даны в таблице.
Построить графики величин, указанных в таблице:
| Вариант | Еm, В | n | Е0, В | R1, Ом | R2, Ом | Построить графики в функции времени |
| д | 1,4 | i1, i2 |
1) Напишем систему уравнений по Законам Кирхгофа для мгновенных значений величин:
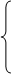
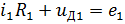
2) Рассмотрим работу схемы на разных участках ВАХ диода
Участок (0-1): 
(диод открыт)
 |
0,05-0,14sinωt 0,2sinωt
0,2 
0,1
0,05
ωt1=210 159 ωt
0 900 1800 2700 3600
-0,1
-0,2
 |
Заключение:
При расчёте переходного процесса в линейной электрической цепи и в классическом, и в операторном методе пришли к одному и тому же решению. Оба эти метода можно применять для решения задач любой сложности. Каким из них пользоваться, во многом зависит от навыка и привычки. Однако, классический метод физически более прозрачен, чем операторный, в котором решение уравнений во многом формализовано. Если при сравнении этих методов исходить из объёма вычислительной работы, то решение уравнений первого, второго, а иногда и третьего порядков для источников постоянной (синусоидальной) ЭДС или тока целесообразно проводить классическим методом, а решение уравнений более высоких порядков - операторным. Объясняется это тем, что чем выше порядок характеристического уравнения, тем более громоздкой и трудоёмкой оказывается операция нахождения постоянных интегрирования в классическом методе. Операторный метод имеет перед классическим явное преимущество при решении задач, в которых определение принуждённой составляющей искомой величины оказывается затруднительным вследствие сложного характера принуждающей силы.
Расчет и исследование нелинейных цепей во многих случаях производят графо-аналитическими методами, в основу которых положены законы Кирхгофа. Если ВАХ НС выражена аналитической функцией, то может быть выполнен и аналитический расчет (на основании законов Кирхгофа). При расчете нелинейных цепей вводят понятие статического и динамического (дифференциального) сопротивлений нелинейного элемента.
Список литературы и интернет-ресурсы
1. Бессонов Л. А. Теоретические основы электротехники: Электрические цепи: Учебник / Л.А. Бессонов. - М.: Юрайт, 2012.
2. Бессонов Л.А., Демидова И.Г., Заруди М.Е. и др. Сборник задач по теоретическим основам электротехники. - М.: Высшая школа, 2000.
3. Прянишников В.А., Петров Е.А., Осипов Ю.М. Электротехника и ТОЭ в примерах и задачах: Практическое пособие. - КОРОНА принт, 2003.
4.Теоретические основы электротехники: Методические указания и контрольные задания для студентов технических специальностей вузов / Л.А. Бессонов, И.Г. Демидова, М.Е. Заруди и др. - М.: Высш. шк., 2003.
