Задача 1.
Дано:
|
|
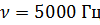
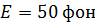
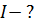
Решение:
Используя зависимость уровня громкости от звукового давления и частоты:
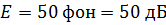
Из формулы:
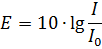
Где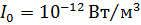 
Найдем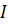 
:
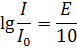
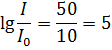
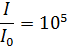
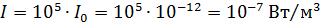
Ответ: 
.
Задача 2.
Поток веществ через мембрану подчиняется уравнению Теорелла:
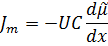
Подставив сюда уравнение для электрохимического потенциала получаем:
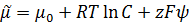
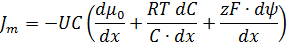
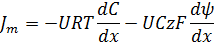
Последнее выражение и есть уравнение Нернста-Планка, оно показывает две причины переноса веществ через мембрану: градиент концентрации и градиент электрического потенциала.
Подход Планка-Гендельсона предполагает электронейтральность мембраны и равенство концентраций катионов и анионов по разные стороны мембраны. Следовательно, равенство потоков катионов и анионов, тогда:
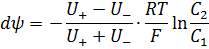
Годьдман предположил линейность электрохимического потенциала в толще мембраны:
Тогда решение уравнения для концентрации иона на краях мембраны будет таким:
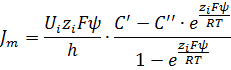
Ходжкин в дальнейшем предположил, что концентрация ионов на краях мембраны пропорциональны концентрациям в соответствующих растворах.
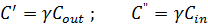
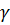– коэффициент липофильности.
Тогда уравнение Гольдмана преобразуется:
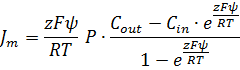
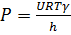- коэффициент проницаемости.
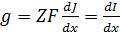– проводимость.
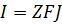– электрический ток.
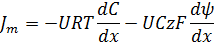
Уравнение Нернста-Планка показывает две причины переноса веществ через мембрану: градиент концентрации и градиент электрического потенциала. Для неполярных веществ (z = 0) формула сводится к закону диффузии Фика:
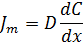
Закон диффузии Фика показывает, что транспорт неполярных веществ молекул зависит только от проницаемости молекул, что выражается в коэффициенте диффузии, и пропорционален разности концентраций.
Существует три механизма пассивного транспорта неполярных веществ: простая диффузия, облегченная диффузия и фильтрация.
Простая диффузия неполярных веществ не требует наличия специальных структур и зависит только от растворимости в липидах – липофильности – и от вязкости мембраны.
Облегченная диффузия для неполярных веществ происходит с участием специальных переносчиков. Этот процесс может происходить в симпорте или антипорте с другими веществами.
Транспорт через поры или каналы – специальные мембранные структуры, транспорт через которые зависит только от градиента концентрации. Каналы являются регулируемыми структурами.
В то же время возможен и активный транспорт неполярных веществ против градиента их концентрации.
Задача 3.
Дано:
|
|
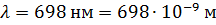
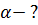
Решение:
Найдем угол между поверхностями клина из формулы для нахождения ширины интерференционного максимума:
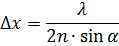
При малых углах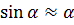 
, значит 
радиан.
Задача 4.
Дано:
|
|
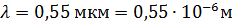
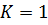
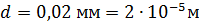
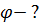
Решение:
Из условия максимума для дифракционной решетки:
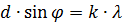
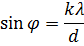
Ответ: 
.
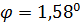Задача 5.
Дано:
|
|
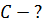
Решение:
Найдем объемно-массовую концентрацию из формулы:
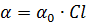
Ответ: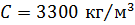 
.
Задача 6.
Дано:
|
|
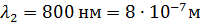
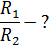
Решение:
Так как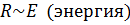 
, где 
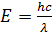, то
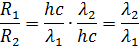
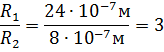
Ответ: Энергетическая светимость усилилась 3 раза.
Задача 7.
Дано:
|
|
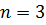
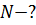
Решение:
Атом может испустить два кванта при переходе с n = 3 на n = 2, и с n = 3 на n = 1
Задача 8.
Дано:
|
|
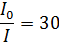
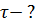
Решение:
Найдем время жизни молекулы в возбужденном состоянии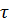 
из уравнения:
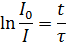
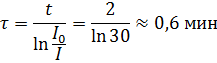
Ответ: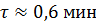 
Задача 9.
Дано:
|
|
Решение:
По закону сохранения энергии:
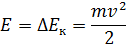
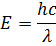
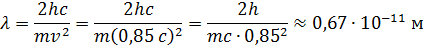
Ответ: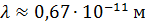 
.
Задача 10.
Дано:
|
|
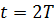
Решение:
По закону радиактивного распада:
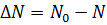
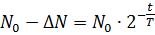
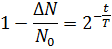
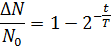
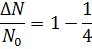
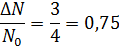
Ответ: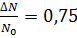 
ГБОУ ВПО «Смоленская государственная медицинская академия»
Кафедра медицинской и биологической физики
Физика
Контрольная работа № 1
Вариант № 32
Выполнила: студентка 1 курса
2 группы
фармацевтического факультета
Борисова Анна
Проверила: Деревцова С.Н.
Оценка:
Смоленск 2012
