Отчет по лабораторной работе №1
«Определение ускорения свободного падения с помощью математического маятника»
Цель работы:
- изучение законов колебания математического маятника;
- научиться производить прямые и косвенные измерения;
- научиться производить расчеты погрешностей при проведении прямых и косвенных измерений;
- измерить ускорение свободного падения (на широте г. Ижевска).
Краткое изложение теоретических предпосылок для проведения работы:
Математический маятник – это система, состоящая из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения.
Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен,

И не зависит от амплитуды и массы маятника.
Приборы и принадлежности
Приборы:
- Линейка цена деления 1,0 мм;
- Секундомер цена деления 0,1 сек.
Принадлежности:
1 – массивное основание;
2 – стойка;
3 – подвес (нитка считается
абсолютно нерастяжимой и невесомой);
4 – груз математического маятника;
L – длина подвеса.
Расчетные формулы и соотношения
Прямые измерения
Прямое измерение — измерение, при котором искомое значение физической
величины получают непосредственно.
Среднее значение 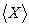 измеряемой величины X производится по формуле:
измеряемой величины X производится по формуле:
 (1),
(1),
где 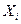 – измеренное значение величины (непосредственно измеренное тем или иным измерительным прибором);
– измеренное значение величины (непосредственно измеренное тем или иным измерительным прибором);
i – номер измерения;
n – число непосредственных измерений в проводимом эксперименте.
Случайная ошибка измеряемой величины 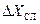 (при прямых измерениях) определяется по формуле:
(при прямых измерениях) определяется по формуле:
 (2),
(2),
где  – коэффициент Стьюдента для числа измерений равному n и уровне доверительной вероятности P =95% (берется из таблиц для соответствующих n и P).
– коэффициент Стьюдента для числа измерений равному n и уровне доверительной вероятности P =95% (берется из таблиц для соответствующих n и P).
Приборная ошибка при прямых измерениях  определяется по формуле:
определяется по формуле:
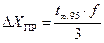 (3),
(3),
где 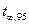 – коэффициент Стьюдента для бесконечного числа измерений и уровне доверительной вероятности P =95% (берется из таблиц для соответствующих n и P),
– коэффициент Стьюдента для бесконечного числа измерений и уровне доверительной вероятности P =95% (берется из таблиц для соответствующих n и P),
f – цена деления измерительного прибора.
Полная ошибка при измерениях 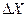 (прямых) определяется по формуле:
(прямых) определяется по формуле:
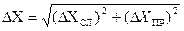 (4),
(4),
Если какая-либо из ошибок превосходит другую в 10 и более раз, то при определении полной ошибки по формуле (4) меньшей ошибкой можно пренебречь.
Результат прямого измерения представляется в виде:
Величина 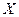 (длина подвеса) равна
(длина подвеса) равна 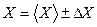 при доверительной вероятности 95% (5),
при доверительной вероятности 95% (5),
Косвенные измерения
Косвенное измерение — это определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
В настоящей лабораторной работе проведены косвенные измерения следующих величин:
- период колебаний математического маятника 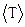 ;
;
- ускорение свободного падения  .
.
Измерение периода колебаний математического маятника 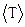 (косвенные измерения) проводится по формуле:
(косвенные измерения) проводится по формуле:
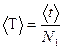 (6),
(6),
где 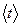 – время
– время  полных колебаний математического маятника;
полных колебаний математического маятника;
 – число полных колебаний математического маятника.
– число полных колебаний математического маятника.
Определение погрешности (ошибки) измерения периода колебаний математического маятника  (косвенные измерения) проводится по формуле:
(косвенные измерения) проводится по формуле:
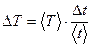 (7).
(7).
Результат измерения представляется в виде:
период колебаний математического маятника равен 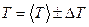 при доверительной вероятности 95%
при доверительной вероятности 95%
Определение (измерение) ускорения свободного падения  в поле тяжести Земли (косвенное измерение) проводится по формуле
в поле тяжести Земли (косвенное измерение) проводится по формуле
 (8),
(8),
где 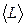 – результат прямого измерения длины подвеса математического маятника,
– результат прямого измерения длины подвеса математического маятника,
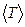 – период свободных колебаний математического маятника (результат косвенного измерения),
– период свободных колебаний математического маятника (результат косвенного измерения),
Определение ошибки измерения ускорения свободного падения 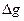 (косвенное измерение) проводится по формуле:
(косвенное измерение) проводится по формуле:
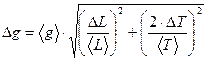 (9).
(9).
Результат измерения представляется в виде:
ускорения свободного падения равно 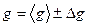 при доверительной вероятности 95%
при доверительной вероятности 95%
Выполнение работы
Этап 1: измерение длины подвеса 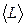 математического маятника (прямое измерение)
математического маятника (прямое измерение)
Линейкой измерили длину маятника (от точки подвеса до центра шарика).
В ходе выполнения данного этапа было проведено 5 измерений длины подвеса математического маятника 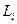 . Результаты представлены в графе 2 таблицы 1.
. Результаты представлены в графе 2 таблицы 1.
Таблица 1.
| Номер измерения (непосредственные измерения) | 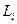 ,(мм) ,(мм)
|  ,(мм) ,(мм)
| 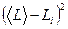 , (мм) , (мм)
|
| 0,4 | 0,16 | ||
| 1,4 | 1,96 | ||
| -1,6 | 2,56 | ||
| -0,6 | 0,36 | ||
| 0,4 | 0,16 | ||
 496,4 496,4
| 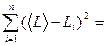 5,2 5,2
|
Среднее значение длины подвеса математического маятника 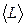 определялось по формуле (1):
определялось по формуле (1):
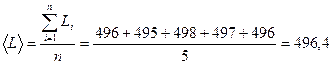 (мм);
(мм);
Случайная ошибка измерения длины подвеса математического маятника 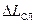 определялась по формуле (2):
определялась по формуле (2):

где  =2,8
=2,8
Приборная ошибка при измерениях 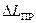 определяется по формуле (3):
определяется по формуле (3):
 (мм)
(мм)
где 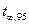 =2,0
=2,0
f = 1,0 мм
Полная ошибка измерения определяется по формуле:
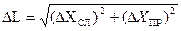
 ≈1,6мм
≈1,6мм
Отсюда  = 1,6 (мм)
= 1,6 (мм)
Таким образом, полученный результат:
 496,4 + 1,6 (мм)
496,4 + 1,6 (мм)
Этап 2: определение времени 20-ти полных колебаний математического маятника t (прямое измерение)
1. Отклонив маятник от положения равновесия на 5-8 градусов, предоставив ему возможность свободно колебаться.
2. В момент наибольшего отклонения маятника пускают в ход секундомер и отсчитывают время 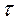 , в течение которого маятник совершает N=20 полных колебаний. В ходе выполнения данного этапа было проведено 5 отсчетов времени 20-ти полных колебаний
, в течение которого маятник совершает N=20 полных колебаний. В ходе выполнения данного этапа было проведено 5 отсчетов времени 20-ти полных колебаний 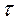 .Результаты представлены в графе 2 таблицы 2.
.Результаты представлены в графе 2 таблицы 2.
Таблица 2.
| № п/п | Измеренные значения, 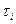 (с) (с)
|  (с) (с)
| ( ) )  (с) (с) 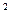
|
| 1. | 28,3 | -0,1 | 0,01 |
| 2. | 28,3 | -0,1 | 0,01 |
| 3. | 28,0 | 0,2 | 0,04 |
| 4. | 28,4 | -,02 | 0,04 |
| 5. | 28,0 | 0,2 | 0,04 |
 28,2 28,2
| 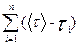 =0,14 =0,14
|
Среднее значение времени 20-ти полных колебаний математического маятника <t> определялось по формуле (1):
 28,2 (сек)
28,2 (сек)
Случайная ошибка измерения времени 20-ти полных колебаний математического маятника 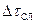 определялась по формуле (2):
определялась по формуле (2):
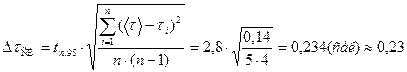 (сек)
(сек)
где  =2,8
=2,8
Приборная ошибка при измерениях 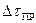 определяется по формуле (3):
определяется по формуле (3):
 (сек)
(сек)
где 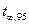 =2,0
=2,0
f = 0,1 сек
Полная ошибка при измерении 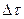 определялась по формуле (4):
определялась по формуле (4):
 0,24 (сек) ≈ 0,2 (сек)
0,24 (сек) ≈ 0,2 (сек)
Таким образом, полученный результат:
 28,2 + 0.2 (сек)
28,2 + 0.2 (сек)
Этап 3: определение периода колебаний T математического маятника (косвенное измерение)
Период колебаний математического маятника определялся по формуле (6):
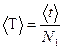 =
= 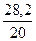 =1,410(сек)≈1,41(сек)
=1,410(сек)≈1,41(сек)
Определение погрешности (ошибки) измерения периода колебаний математического маятника  (косвенные измерения) проводится по формуле (7):
(косвенные измерения) проводится по формуле (7):
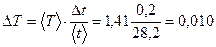 (сек) ≈0,01(сек)
(сек) ≈0,01(сек)
Таким образом, полученный результат:
Т=1,41±0,01 (сек)
Этап 4: определение ускорения свободного падения в поле сил тяжести Земли на широте г. Ижевска (косвенное измерение)
Измерение ускорения свободного падения  в поле тяжести Земли (косвенное измерение) проводится по формуле (8):
в поле тяжести Земли (косвенное измерение) проводится по формуле (8):
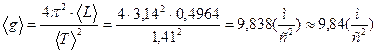
Определение ошибки измерения ускорения свободного падения 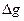 (косвенное измерение) проводится по формуле (9):
(косвенное измерение) проводится по формуле (9):
Таким образом полученный результат:
g=9,84±0,14 (м/с²)
Подведение итогов выполнения лабораторной работы
В результате проведения лабораторной работы были:
1. изучены законы колебательно движения математического маятника;
2. проведены измерения (прямые) длины подвеса математического маятника, времени 20-ти полных колебаний математического маятника.
3. проведены измерения (косвенные) периода колебания математического маятника, ускорения свободного падения на широте г. Ижевска.
4. полученное значение ускорения свободного падения составило:
g=9,84±0,14 (м/с²). Полученное значение соответствует значению ускорения свободного падения на широте города Ижевска равное,
g=9,815847326 м/с², рассчитанное по формуле:
Реальное ускорение свободного падения на поверхности Земли зависит от широты, высоты над уровнем моря и других факторов. Оно может быть вычислено (в м/с²) по формуле: 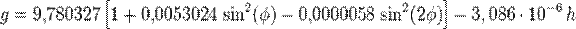
где 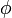 — широта рассматриваемого места,
— широта рассматриваемого места,  — высота над уровнем моря в метрах. (Ю.Н. Сарайский. Геоинформационные основы навигации: Учебное пособие. Санкт-Петербург, 2010г. с. 20.)
— высота над уровнем моря в метрах. (Ю.Н. Сарайский. Геоинформационные основы навигации: Учебное пособие. Санкт-Петербург, 2010г. с. 20.)
Географические параметры г. Ижевска необходимые для расчетов: Широта 56o50'. Высота над уровнем моря: 159м.
Произведем расчет ускорения свободного падения для географических параметров г. Ижевска
gizhevsk= 9,780327(1+0,0053024*sin56,5* sin56,5 – 0,0000058* sin113* sin113)– 3,086*159/1000000 = 9,815847326 м/с²
Вывод: Расчетное значение ускорения свободного падения входит в допустимый интервал значений полученных в лабораторной работе.
9,7 ≤ 9,815847326 ≤ 9,98
Следовательно, измерения и расчеты ускорения свободного падения, выполненные в лабораторной работе верны.
входит в найденный промежуток [9.7…9.98].






