Магнитное поле
В пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным.
Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием поля, создаваемого током (это явление впервые обнаружено датским физиком X. Эрстедом (1777—1851)).
Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды.
Особенностью магнитного поля является то, что оно действует только на движущиеся в этом поле электрические заряды. Характер воздействия магнитного поля на ток зависит от формы проводника, по которому течет ток, расположения проводника и направления тока.
При исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле (рис.15.1). Ориентация контура в пространстве определяется направлением нормали к  контуру. Направление нормали определяется правилом правого винта: за положительное нап-равление нормали при-нимается направление поступательного дви-жения винта, головка которого вращается в направлении тока, текущего в рамке.
контуру. Направление нормали определяется правилом правого винта: за положительное нап-равление нормали при-нимается направление поступательного дви-жения винта, головка которого вращается в направлении тока, текущего в рамке.
 Магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая её определенным образом. Этот результат используется для выбора направления магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль кото-рого располагается положительная нормаль к рамке(рис.15.2).
Магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая её определенным образом. Этот результат используется для выбора направления магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль кото-рого располагается положительная нормаль к рамке(рис.15.2).
За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.
Рамкой с током можно воспользоваться также и для количественного описания магнитного поля.
Так как рамка с токомиспытывает ориентирующее действие поля, то на нее в магнитном поле действует пара сил. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой
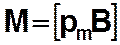 , (15.1)
, (15.1)
где pm — вектор магнитного момента рамки с током; В — вектор магнитной индукции (количественная характеристика магнитного поля). Для плоского контура с током I
 , (15.2)
, (15.2)
где S - площадьповерхности контура (рамки), n - единичный вектор нормали к поверхности рамки. Направление pm совпадает, таким образом, с направлением положительной нормали.
Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на нихдействуют различные вращающие моменты, однако отношение 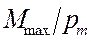 (M max. - максимальный вращающий момент) для всех контуров одно и то же и поэтому оно может служить характеристикой магнитного поля. Эта характеристика магнит-ного поля получила называние магнитной индукцией:
(M max. - максимальный вращающий момент) для всех контуров одно и то же и поэтому оно может служить характеристикой магнитного поля. Эта характеристика магнит-ного поля получила называние магнитной индукцией:
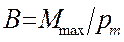 .
.
Магнитная индукция вданной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля.
Следует отметить, что вектор В может быть выведен также из закона Ампера и из выражения для силы Лоренца.
Так как магнитное поле является силовым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции. Это такие линии, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.
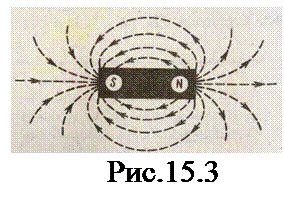 Линии магнитной индукции можно ²проявить² с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам.
Линии магнитной индукции можно ²проявить² с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам.
Линии магнитной индукции всегда замкнуты и охватывают проводники с током. Этим они отличаются от линий напряжен-ности электростатического поля, которые являются разомкнутыми (начинаются на положительных зарядах и кончаются на отрицательных).
До сих пор мы рассматривали макроскопические токи, текущие в проводниках. Однако, согласно предположению французского физика А. Ампера (1775—1836), в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Эти микроскопические молекулярные токи создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т. е. при одном и том же токе и прочих равных условиях вектор В в различных средах будет иметь разные значения.
Магнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индук-ции связан с вектором напряженности следу-ющим соотношением:
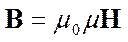 , (15.3)
, (15.3)
где m 0 - магнитная постоянная, m - безразмер-ная величина - магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды.
Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор магнитной индукции В, так как векторы Е и В определяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля.
 15.2. Закон Био‑Савара‑Лапласа
15.2. Закон Био‑Савара‑Лапласа
Магнитное поле постоянных, токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
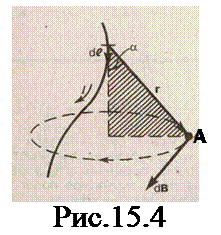 Закон Био‑Савара‑Лапласа. Выделим на проводнике с током I, элемент d l. Этот элемент создает в некоторой точке А (рис.15.4)
Закон Био‑Савара‑Лапласа. Выделим на проводнике с током I, элемент d l. Этот элемент создает в некоторой точке А (рис.15.4)
индукцию поля
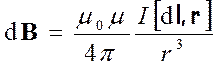 , (15.4)
, (15.4)
где 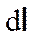 — вектор, по модулю равный длине d l элемента проводника и совпадающий по направлению с током, r - радиус-вектор, проведенный из элемента d l проводника в точку А поля, r - модуль радиуса-вектора r. Направление d B перпенди-кулярно плоскости, в которой лежат векторы d l и r, и совпадает с касательной к линии магнитной индукции. Это направление опре-деляется по правилу правого винта: направле-ние вращения головки винта дает направление d B, если поступательное движение винта соответствует направлению тока в элементе.
— вектор, по модулю равный длине d l элемента проводника и совпадающий по направлению с током, r - радиус-вектор, проведенный из элемента d l проводника в точку А поля, r - модуль радиуса-вектора r. Направление d B перпенди-кулярно плоскости, в которой лежат векторы d l и r, и совпадает с касательной к линии магнитной индукции. Это направление опре-деляется по правилу правого винта: направле-ние вращения головки винта дает направление d B, если поступательное движение винта соответствует направлению тока в элементе.
Модуль вектора d B определяется выраже-нием
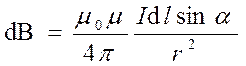 , (15.5)
, (15.5)
где a — угол между векторами d l и r.
Принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися заряда-ми, равна векторной сумме магнитных индук-ций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
 . (15.6)
. (15.6)
 Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока име-ет определенную симметрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля.
Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока име-ет определенную симметрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля.
Рассмотрим два примера.
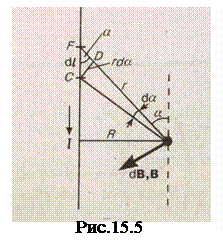
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис.15.5). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы d B от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов d B можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами d l и r), выразив через него все остальные величины. Из рис.14.5 следует, что
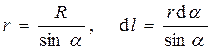
(радиус дуги CD вследствие малости d l равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (14.5), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
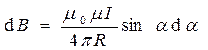 . (15.7)
. (15.7)
Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то согласно (14.6) и (14.7),
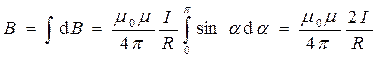 .
.
Следовательно, магнитная индукция поля прямого тока
 . (15.8)
. (15.8)
2.Магнитное поле в центре кругового проводника с током (рис.15.6). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin a =l) и расстояние всех элементов проводника до центра кругового тока одинаково и 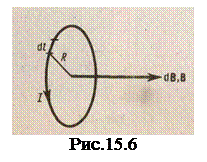 равно R, то, согласно (15.5),
равно R, то, согласно (15.5),
 .
.
Тогда  .
.
Следовательно, магнитная индукция поля в центре круглого проводника с током

 .
.






