ЮЖНЫЙ ФИЛИАЛ
«КРЫМСКИЙ АГРОТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра Геодезии и геоинформатики
Курсовой проект по геодезии
на тему: «Уравновешивание геодезических сетей сгущения и систем ходов плановой съемочной сети»
Проект выполнила:
Студент (ка)) группы К-
Проект принял:
старший преподаватель кафедры землеустройства и
геодезии
Старший преподаватель
Нечаев В.А.
г. Симферополь2013 г.
СОДЕРЖАНИЕ
Введение Часть 1.
Уравновешивание триангуляции 2 разряда.
1.1. Предварительная математическая обработки измерений.
1.2. Уравнивание триангуляции 2 разряда.
Отчетная схема триангуляции 2 разряда. Часть 2. Уравновешение систем ходов плановой съемочной сети.
2.1. Уравновешивание системы теодолитных ходов с одеон узловой точкой.
2.2. Уравновешивание углов сети теодолитных ходов по способу полигонов профессора В.В.Попова.
2.3. Уравновешивание системы полигонометрических ходов способом последовательных приближений.
Введение
Курсовой проект состоит из двух частей.
1. Уравновешивание триангуляции 2 разряда.
2. Уравновешивание систем ходов плановой съемочной сети.
Часть 1. Уравновешивание триангуляции 2 разряда.
1.1. Предварительная математическая обработка измерений. 1.1.1. Исходные данные.
На рисунке 1 приведена схема триангуляции 2-го разряда. Пункт полигонометрии «Марьино» является пунктом геодезической сети высшего разряда Сторона между пунктами «Марьино» и «Луговое» является исходной.
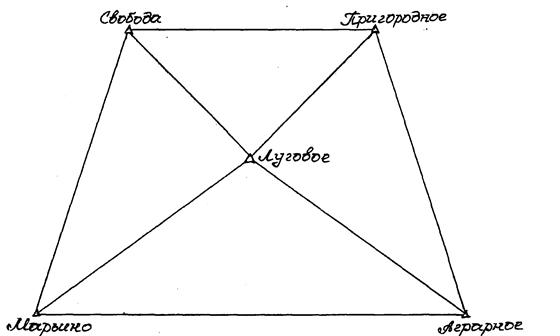
Рис 1. Схема триангуляции 2-го разряда
В таблице 1 представлены координаты опорного пункта «Марьино» и результаты полевых измерений длины исходной стороны и ее направления.
Таблица!
Исходные данные по вариантам
| № | Название пункта | Координаты | Длина исходной стороны,d(м) | Дирекционный угол, α | На какой пункт | |
| Х | ү | |||||
| Марьино | Луговое |
1.1.2. Порядок вычислений.
1.1.2.1. Составить первую рабочую схему исполненной сети (рис. 2) на которую выписать из таблицы 2 измеренные направления
ис 2. Рабочая схема 1 (углы измеренные)
1.1.2.2. На схеме намечаем исходную (твердую) сторону, пронумеровываем треугольники, обозначаем промежуточные стороны и углы.
Таблица 2 Измеренные элементы приведения и направления
| Название пунктов | Элементы приведения | Название направлений | Измеренные направления |
| Аграрное | E= e1= | Луговое | 0˚ 00΄ 00˝ |
| Q= на Луговое; | Пригородное | 35 20 07 | |
| Q1= на Луговое; | Марьино | 341 13 00 | |
| Марьино | E= e1= | Свобода | 0˚ 00 00˝ |
| Q= | Луговое | 26 16 37 | |
| Q1= на Свободу | Аграрное | 95 42 18 | |
| Свобода | E= e1= | Пригородное | 0˚ 00΄ 00˝ |
| Q= | Луговое | 99 00 30 | |
| Q1= на Пригородное | Марьино | 116 24 47 | |
| Луговое | E= e1= | Пригородное | 0˚ 00΄00˝ |
| Q= на Пригородное наПригороднПригородное | Аграрное | 93 30 39 | |
| Q1= на Пригородное | Марьино | 185 17 59 | |
| Свобода | 321 37 05 | ||
| Пригородное | E= e1= | Аграрное | 0˚ 00΄ 00˝ |
| Q= | Луговое | 51 09 14 | |
| Q1= на Аграрное | Свобода | 93 45 48 |
Примечание: Значения угловых элементов приведения θ и е на каждом пункте выписываем в таблицу 2 в соответствии со своим вариантом из приложения.
1.1.2.3. По данным таблицы 2 вычисляем измеренные углы и выписываем их значения на рабочую схему (см. рис 2.)
1.1.2.4. Вычисленные значения углов выписываем с округлением до 2х знаков после запятой в бланк предварительного решения треугольников в порядке нумерации, указанной в таблице 3. Длину исходной стороны выписываем с округлением до 10 м в одной строке с противоположным углом.
1.1.2.5. Подсчитываем сумму углов по каждому треугольнику. Если она отличается (за счет ошибок округления) от 180° не более чем Г, то находим синусы углов (с тремя десятичными знаками).
1.1.2.6. По теореме синусов вычисляем стороны треугольников, начиная с первого, по формулам:
ai=Di sin A
bi=Di sin A (1)
ci=Di sin A
в которых Di - постоянный коэффициент для 1 треугольника, определяемый соотношением:
 (2)
(2)
Контролем решения треугольников является сходимость длины исходной стороны bi с вычисленным значением в a1
Расхождение не должно быть (для данной сети) более 10 метров, т.е. ∆ B= b1 - a4 ≤ 10 м (см. таблицу 3).
1.1.2.7. В бланк вычисления поправок за центрировку и редукцию (таблица 4) выписать в соответствии со своим вариантом из таблицы 2 линейные и угловые элементы приведения. Цифрами в скобках указан порядок записи и решения.
В каждой графе таблицы 4 записываем название пункта по измерению, начиная с начального и в строку 5, в том же порядке выписываем из ведомости измеренных величин (таблица 2) значения измеренных направлений М.
Таблица 3
Предварительное решение треугольников
| № тр | Название пунктов | № углов | Углы | Синусы углов | Длины сторон |
| Свобода | |||||
| Луговое | |||||
| Марьино | |||||
| Пригородное | |||||
| Луговое | |||||
| Свобода | |||||
| Аграрное | |||||
| Луговое | |||||
| Пригородное | |||||
| Марьино | |||||
| Луговое | |||||
| Аграрное | |||||
1.1.2.8. Из бланка предварительного решения треугольников (таблица 3) выписываем расстояния S (строка 8), находим суммы Q+M и M+Q1, вычисляем значения
k=e p˝ (3)
k=e1 p˝ (4)
а затем k:s и k1:s
| По формулам: |
| (5) |
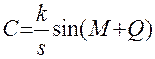
и
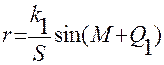
вычислить поправки за центрировку e˝ и редукцию
Вычисление поправок за центрировку и редукцию
| №№ п.п | п. Пригородное | |||||||
| E= e1= на пункт Аграрное Q= Q1= K=ep˝= k1=e1p˝ | ||||||||
| На пункт обозначения | Аграрное | Луговое | Свобода Свобода | |||||
| (10) (6) (5) (7) (9) | M+Q1 Q1 M Q M+Q | |||||||
| (17) (15) (13) (8) (14) (16) | r˝ sin(M+Q1) k1:s s k:s sin(M+Q) | |||||||
| (18) | c˝ | |||||||
| №№ п.п. | п, Луговое | |||||||
| E= e1= -на пункт Пригородное Q= Q1= K=ep˝= k1=e1p˝ | ||||||||
| На пункт обозначения | Пригородноеее | Аграрное Марьино | марьино | Свобода | ||||
| (10) (6) (5) (7) (9) | M+Q1 Q1 M Q M+Q | |||||||
| (17) (15) (13) (8) (14) (16) | r˝ sin(M+Q1) k1:s s k:s sin(M+Q) | |||||||
| (18) | с˝ | |||||||
| №№ п.п | п. Аграрное | |||||||
| E= e1= на пункт Луговое Q= Q1= K=ep˝= k1=e1p˝ | ||||||||
| На пункт обозначения | Луговое | Пригородное | Марьино | |||||
| (10) (6) (5) (7) (9) | M+Q1 Q1 M Q M+Q | |||||||
| (17) 05) (13) (8) (14) (16) | r˝ sin(M+Q1) k1:s s k:s sin(M+Q) | |||
| (18) | ||||
| №№ П.П | п. Марыию | |||
| E= e1= -на пункт Свобода Q= Q1= K=ep˝= k1=e1p˝ | ||||
| На пункт обозначения | Свобода | Луговое | Аграрное | |
| (10) (6) (5) (7) (9) | M+Q1 Q1 M Q M+Q | |||
| (17) (15) (13) (8) (14) (16) | r˝ sin(M+Q1) k1:s s k:s sin(M+Q) | |||
| (18) | ||||
| №№ П.П. | п- Свобода Пригородное | |||
| E= e1= -на пункт Пригородное Q= Q1= K=ep˝= k1=e1p˝ | ||||
| На пункт обозначения | Приторное | Луговое | Марьино | |
| (10) (6) (5) (7) (9) | M+Q1 Q1 M Q M+Q | |||
| (17) (15) (13) (8) (14) (16) | r˝ sin(M+Q1) k1:s s k:s sin(M+Q) | |||
| (18) | С" | — | — | — |
Величины М, M+Q, M+Q1, C" и r" вычислить с точностью: М, М + Q, -до целых минут, e˝ и r˝ до десятых долей угловой секунды
1.1.2.9. По результатам полевых измерений (см. таблицу 2), а также на основании рабочей схемы сети (см. рис. 2) и вычисленных значений поправок за центрировку и редукцию (см. таблицу 4) привести измеренные направления М На каждом пункте к центру к центрам пунктов (таблица5). Поправки за центровку вводим в измеренные направления на том пункте, на котором были определены элементы центрировок с", О; поправка за редукцию вводят на пункте наблюдения в измеренные направления на те пункты, на которых были определены элементы редукции.
1.1.2.10. Из таблицы 2 выписываем в ведомость вычисления приведенных направлений (таблица 5) названия пунктов и измеренные направления. Сначала записываем и подчеркиваем название пункта, на котором произведены измерения, а под ним названия наблюдаемых с него пунктов 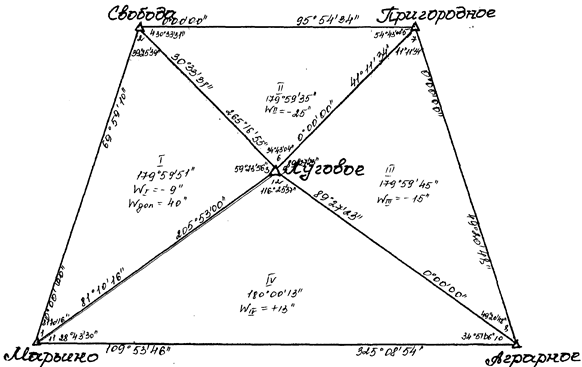
Таблица 5
Приведение направлений к центрам пунктов
| № № П.П | Название направлений | Измеренные направления (М) | Поправки за приведения | приведенные направления | ||||
| с | r | (с+r) | (с+r)- (с+r)0 | |||||
| Аграрное | ||||||||
| Луговое Пригородное Марьино | ||||||||
| Марьино | ||||||||
| Свобода Луговое Аграрное | ||||||||
| Свобода | ||||||||
| Пригородное Луговое Марьино | ||||||||
| Луговое | ||||||||
| Пригородное Аграрное Марьино Свобода | ||||||||
| Пригородное | ||||||||
| Аграрное Луговое Свобода |
Вычислить приведенные направления по формуле  M = M +(e + r) + (e + r)0
M = M +(e + r) + (e + r)0
По данным табл. 5 на вторую рабочую схему триангуляции вписать приведенные направления и по ним вычислить приведенные углы.
Вычислить по приведенным углам и выписать в каждом треугольнике сумму углов, невязку и W1 и сравнить её с допустимой 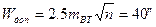
По формуле Ферерро вычислить СКО измеренного угла по невязкам W в треугольниках 
Где N- число треугольников.




