| № № п. п. | Название пункта тип я высота знака тип центра | Разряд | Координаты Х, м У, м | Длина сторон | Дирекционныеуглы | На пункт |
| Свобода пир.6,2м центр 2 типа | Приигородное Луговое Марьино | |||||
| Пригородное пир.6,8м центр 2 типа | Аграрное Луговое Свобода | |||||
| Аграрное пвр,6,5м центр 2 типа | Пригородное Марьиво | |||||
| Луговое пир.6,3м центр 2 типа | Марьино Свобода | |||||
| Марьино пир 6,6м центр 2 типа | Луговое Аграрное Свобода |
Выписал
Считал:
.
Часть II* Уравновешивание систем ходов плановой съемочной сети*
2.1. Уравновешивание систем теодолитных ходов с одной узловой точкой. 2.1.1. Задание.Произвести уравновешивание систем теодолитных ходов, сходящихся в узловой точке 3 и опирающихся на линии геодезической сети АВ, СD, ЕF с известными дирекционными углами и пункты В, О и Р представлены по вариантам в таблице 11. Схема ходов и значения измеренных углов и длин линий приведены на рисунке 5.
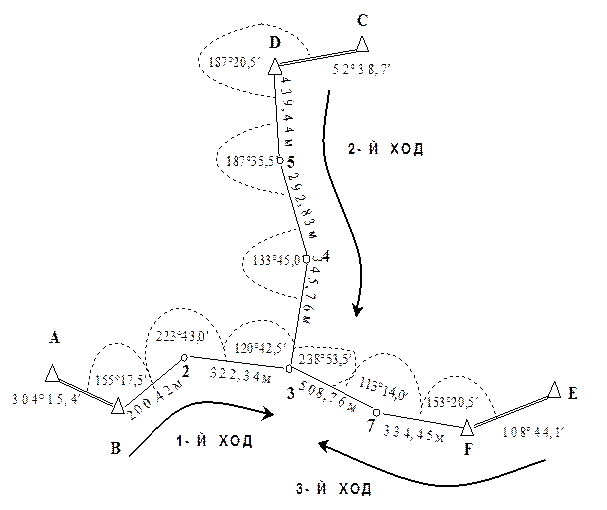
Таблица 11
Исходные данные. 
| № № варианта | Координаты пикетов | Дирекционные углы | |||||||
| В | D | F | AAB | ACD | AEF | ||||
| Х | У | Х | У | X | Y | ||||
Вычисления всех дирекционных углов выполнить с округлением до 0,1'. Приращение координат и координаты вычислить с округлением до 0,01'м. В результате уравнивание сети ходов должны быть представлены:
1. Схематический чертеж (рис. 5)
2. Ведомость вычисления координат (таблица 12).
3. Таблица вычислений окончательных значений дирекционного угла узловой линии (таблица 13).
4. Таблица вычислений окончательных значений координат узловой точки (таблица 14).
2.1.2. Порядок решения.
2.1.2.1. По схеме намечаем узловую линию, например линию 2-3. Выписываем в ведомость координат (таблица 12) измеренные углы (графа 2) и дирекционные углы твердых линий (графа 4). Подсчитываем в графу 2 таблицу 13, а графу 4 записываем число углов л; по каждому ходу.
2.1.2.3. Оцениваем качество угловых измерений» составим для этого разности вычисленных для узловой линии дирекционных углов. Первую разность составляем из дирекционных углов, найденным по двум хода с наименьшим числом углов. Полученная разность равна угловой невязке этих двух ходов. Сравнить эту разность с допустимой невязкой определяемой по формуле:
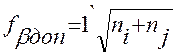
| (23) |
где 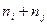 - число углов в обоих ходом.
- число углов в обоих ходом.
Другая разность составляем из дирекционных углов, вычисленных по третьему ходу и одному из двух первых. Эту невязку также сравнивают с предельной, определяемой по формуле (23). Результаты вычислений записываем в графу 9 таблицу 13.
Таблица 12
Ведомость вычисления координат.
| № точек | Углы | Горизонтальное проложение | Приращения координат | Координата! | ||||||
| Измер. | Исправл | Дирекц. | Вычисленные | исправленные | ||||||
| ∆x | ∆y | ∆X | ∆y | X | y | |||||
| 3, | б | |||||||||
| A | (левые) | |||||||||
| B | ||||||||||
 P=
P= 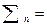
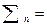
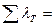
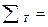
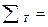
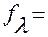
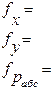
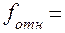

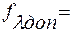
| б | ||||||||||
| C | (врявые) | |||||||||
| D | ||||||||||
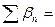 P=
P= 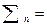
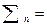
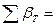
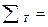
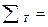

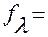
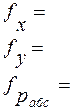
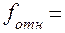

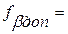
| б | и | |||||||||
| E | (Правые) | |||||||||
| F | ||||||||||
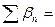 P=
P= 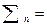
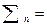
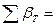
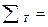
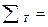

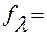
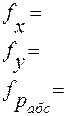
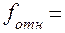

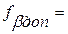
2.1.2.4. Определяем веса вычисленных значений дирекционного угла узловой линии по формуле:
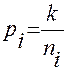 (24).
(24).
где n i - число углов в i - м ходе,
k - произвольный коэффициент, выбираемый так, чтобы веса выражались числами близкими к единице. Найденные веса записываем в графу 5 таблицу 13 с округлением до 0,01.
Таблица 13
Вычисление окончательного значения a3-2
| № ходов | Дирекцион- ные углы | ε, | Число углов | 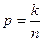 k=12 k=12
| PE | Невязки fβ | pfβ | проверка допустим. угловых. невязок |
| 3 | б | |||||||
a0= [PE]= [Pfβ]=
[P]=
Контроль: ω[P]=
| (25) (26) |
| (27) (28) (29) |
2.1.2.5. По формулам общей арифметической средины:
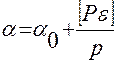
где α0- приближенное значение искомого дирекционного угла ε1 остаток, определяемый по формуле:
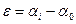 (I=1,2,3)
(I=1,2,3)
вычислить окончательноезначение дирекционного угла α
2.1.2.6. Вычисляем угловые невязки ходом для правых углов поформуле: 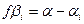
для левых углов по формуле:
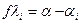
Полученные значения невязок записать в графу 7 таблицы 13. Выполнить контроль вычисления невязок по формуле:
[pfβ] =0
Вследствие ошибок округлений это равенство может не выполняться. В этом случае
[pfβ]=ω[P] (30)
 где ω- ошибка округления при делении [ Pε ] на [ p ].
где ω- ошибка округления при делении [ Pε ] на [ p ].
2.1.2.7. Полученное окончательное значение дирекционного угла а узловой линии в дальнейшем принимают за твердое и записывают в графу 4 таблицы 12. Затем вычислять теоретические суммы углов по каждому ходу по формулам:
• для правых углов
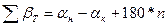
(31)
• для левых углов
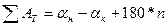
(32)
где αн и αк - начальный и конечный углы хода, найти угловые невязки и сличить их с полученными в графе 7 таблица 12, учитывая, что невязки для правых и левых углов одного и того же хода противоположны по знаку (ход 1).
Если полученные невязки меньше предельных, то распределим их с противоположным знаком поровну на углы соответствующих ходом (с округлением до 0,1').
2.1.2.8. Вычисляем дирекционные углы линий по формулам:
| (33) |
• для правых углов: α1=αi-1+180˚-βi
• для левых углов: α1=αi-1+180˚-λi
Вычисление окончательных значений координат узловой точке 3.
| №№хода | X,м | Εx` см | Pεx` см | Fx` см | Pfx` см | S км | 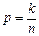 k=4
k=4
| Pfy` см | Fy` см | Pεy` см | Εy` см | Y,м |
| 1 | 3 | 4 | 6 | 9 | ||||||||
X0 = [pεx]= [pfx]= [p]= [pfy]= [pεy]= y0=
X= y=
Контроль ωx[p]= ωy[p]=
2.1.2.9. Вычисляем приращения координат и их суммы (см. таблицу 12), а затем -координаты узловой точки по всем трем хода. Результаты вычислений записать в графы 2 и 13 таблицы 14.
Таблица 14
Проверка допустимости линейных невязок
| №№ ходов | Si+j м | Fx=xi-xj | Fy=yi-yj | fабс | Fотн м |
| 5 | 6 | ||||
| 1+2 | |||||
| 2+3 |
2.1.2.10. Оцениваем качество измерений, вычислив для этого невязки по ходам: по первому - вместе со вторым и по второму - вместе с третьим.
Для этого составляем разности координат по соответствующим парам ходов:
Fx=xi-xj Fy=yi-yj (34)
| (35) |
Одна пара ходов берется с наименьшими периметрами. Подсчеты невязок выписываем внизу таблица 14.
Относительные невязки не должны превышать 1:1000.
2.1.2.11. Вычисляем веса значений координат узловой точки по формуле: 
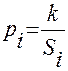
в которой Si - длина соответствующего хода, выражаем в километрах;
k — произвольный коэффициент, выбираем с таким же расчетом, как и при вычислении дирекционных углов. Результаты вычислений записываем в графу 8 таблица 14. 2.1.2.12. По формуле общей арифметической средины:
| (36) |
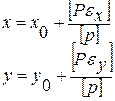
x0 , y0 - приближенные значения координат Х и У.
εxi,εyi - величины определенные по формулам:
εxi=xi-x0 (37)
εyi=yi-y0
вычисляем окончательные значения координат узловой точки Х и У. Полученные значение записываем в таблицу 12.
2.1.2.13. Вычисляем невязки приращений координат для каждого хода по формулам:
f x=xi-x0
f y=yi-y0 (33)
и записываем их в графы 5 и 10 таблицу 14.
Выполняем контроль вычисления Х и У и невязок по формулам:
[p f x]=-ωx[p] (39), [p f y]=-ωy[p] (40)
где ωx и ωy • ошибка округлений при делении [pεx] и [pεy] на [p],
2.1.2.14. Вычисляем для каждого хода в ведомости координат (таблица 12) вторично невязки по формулам:
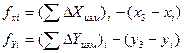 (41)
(41)
где 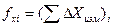 и
и 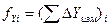 измеренные суммы приращений координат по каждому ходу;
измеренные суммы приращений координат по каждому ходу;
Xi и Yi - координаты начальной точки соответствующего хода;
X3 и Y3 - координаты узловой точки (точка 3).
Эти невязки сличают с полученными ранее.
Данные подсчитываем по каждому ходу fабс и fотн. Если последнее не превышаю 1:1000, то невязки в приращениях координат распределяем на соответствующие приращения с противоположными знаками, пропорционально длине линий.
Затем в графах 8 и 9 таблица 12 вычисляем исправленные приращения координат.
2.1.2.15. По исправленным приращениям координат всех точек (графы 10 и 11 таблица 12).






