ТЕСТЫ
Что является предметом исследования статистики?
а) социально-экономические и технические системы;
б) массовые, социальные и другие сложные явления в системах, изучаемые с помощью статистических данных;
в) группы специально выделенных объектов;
г) предприятия и организации.
Что такое статистический показатель?
а) количественная оценка свойств изучаемого явления, процесса;
б) показатель прогнозируемости явления;
в) специальная оценка наблюдения;
г) качественная оценка свойств изучаемого явления, процесса.
Что такое мониторинг?
а) статистическая обработка результатов наблюдений;
б) систематическое наблюдение за одним или несколькими признаками, характеризующими явление или систему;
в) вероятностная оценка явления;
г) математическое моделирование социально-экономического процесса.
Формула сложения вероятностей для совместных событий?
а) p(A+B) = p(A) + p(B);
б) p(A+B) = p(A) + p(B) + p(AB);
в) p(A+B) = p(A) + p(B) - p(AB);
г) p(A+B) = p(A) + p(B) - 2p(AB).
Формула сложения вероятностей для несовместных событий?
а) p(A+B) = p(A) + p(B);
б) p(A+B) = p(A) + p(B) + p(AB);
в) p(A+B) = p(A) + p(B) - p(AB);
г) p(A+B) = p(A) + p(B) - 2p(AB).
Формула умножения вероятностей для зависимых событий?
а) p(AB) = p(A)p(B);
б) p(AB) = p(A)pА(B);
в) p(AB) = p(B)pB(A);
г) p(AB) = pА(B) pB(A).
Формула умножения вероятностей для независимых событий?
а) p(AB) = p(A)p(B);
б) p(AB) = p(A)pА(B);
в) p(AB) = p(B)pB(A);
г) p(AB) = pА(B) pB(A).
Что такое распределение вероятностей?
а) зависимость значения случайной величины от времени;
б) график изменения случайной величины в зависимости от выбранного фактора;
в) совокупность значений случайной величины и соответствующих им вероятностей;
г) зависимость вероятности от времени.
Что такое плотность вероятности?
а) отношение вероятности к временному диапазону;
б) вероятность, соответствующая единичному интервалу значений случайной величины;
в) отношение вероятности к диапазону изменения выбранного фактора;
г) интеграл вероятности по времени.
Что такое мода?
а) значение признака, приходящегося на середину ранжированной (упорядоченной) совокупности;
б) наиболее вероятное значение случайной вероятности, соответствующее минимуму плотности вероятности;
в) площадь под кривой распределения;
г) наиболее вероятное значение случайной вероятности, соответствующее максимуму плотности вероятности.
Что такое медиана?
а) значение признака, приходящегося на середину ранжированной (упорядоченной) совокупности;
б) наиболее вероятное значение случайной вероятности, соответствующее минимуму плотности вероятности;
в) площадь под кривой распределения;
г) наиболее вероятное значение случайной вероятности, соответствующее максимуму плотности вероятности.
Что такое математическое ожидание?
а) сумма произведений всех возможных значений случайной величины на их вероятности;
б) наиболее вероятное значение случайной вероятности, соответствующее минимуму плотности вероятности;
в) площадь под кривой распределения;
г) сумма произведений всех возможных значений случайной величины на их вероятности.
Что такое дисперсия?
а) математическое ожидание квадрата отклонения случайной величины от ее математического ожидания;
б) сумма произведений всех возможных значений случайной величины на их вероятности;
в) площадь под кривой распределения;
г) значение признака, приходящегося на середину ранжированной (упорядоченной) совокупности.
Что называют средним квадратическим отклонением?
а) интеграл вероятности по времени;
б) квадратный корень из математического ожидания;
в) квадратный корень из дисперсии;
г) сумма произведений всех возможных значений случайной величины на их вероятности.
Что такое асимметрия?
а) отношение центрального момента третьего порядка к кубу среднего квадратического отклонения: 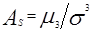 ;
;
б) характеристика, которая определяется равенством: 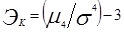 ;
;
в) отношение вероятности к диапазону изменения выбранного фактора;
г) отношение математического ожидания к дисперсии.
Что такое эксцесс?
а) характеристика, которая определяется равенством: 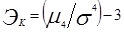 ;
;
б) отношение центрального момента третьего порядка к кубу среднего квадратического отклонения: 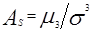 ;
;
в) площадь под кривой распределения;
г) наиболее вероятное значение случайной вероятности, соответствующее максимуму плотности вероятности.
Как выглядит графически нормальное распределение?
а) в виде симметричной кривой;
б) в виде несимметричной кривой;
в) в виде гиперболы;
г) в виде параболы.






