| Способ отбора единиц | ||
| повторный | бесповторный | |
| Средняя ошибка μ: Для средней |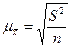 
| 
|
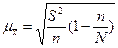
| Для доли |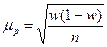 
| 
|
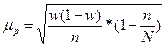
| Предельная ошибка Δ: Для средней |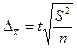 
| 
|
| Для доли |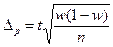 
| 
|
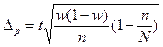
Доверительные интервалы для генеральной средней –
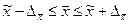
Доверительные интервалы для генеральной доли –
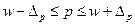
Доверительная вероятность – функция от t, вероятность находится по приложению3
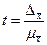
Формулы для определения численности простой и случайной выборки
| Способ отбора единиц | ||
| повторный | бесповторный | |
| Численность выборки (n): Для средней |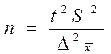 
| 
|
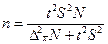
| Для доли* |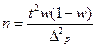 
| 
|
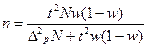
| *В случае, когда частость w даже приблизительно неизвестна, в расчет вводят максимальную величину дисперсии доли, равную 0,25 (если w=0,5, то w(1-w)=0,25). |
Типичная выборка
Применяется в тех случаях, когда из генеральной совокупности можно выделить однокачественные группы единиц (или однородные), затем из каждой группы случайно отобрать определенное число единиц в выборку.
Стандартная среднеквадратическая ошибка:
Повторный отбор -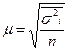 
, 
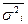- средняя из внутригрупповых
Бесповторный отбор -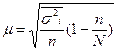 
Отбор единиц при типичной выборке из каждой типичной группы:
1.Равное число единиц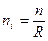 
, 
- число единиц, отобранных из i-ой типичной группы, n – общий объем, R – число групп
2.Пропорциональный отбор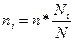 
, 
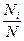- доля i-ой группы в общем объеме генеральной совокупности
3.Отбор единиц с учетом вариации случайного признака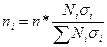 
Серийная выборка
Вместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение.
Средняя стандартная ошибка:
Повторный отбор -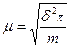 
, 
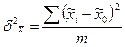, m – число отобранных серий, 
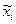- средний уровень признака в серии, 
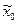- средний уровень признака для всей выборочной совокупности
Бесповторный отбор -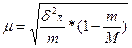 
, M – общее число серий
Малые выборки
Выборки, при которых наблюдением охватывается небольшое число единиц (n<30)
Средняя ошибка малой выборки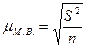 
, 
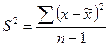
Вероятность того, что генеральная средняя находится в определенных границах, определяется по формуле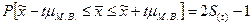 
, 
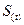- значение функции Стьюдента (приложение 4)
Корреляционная связь
Для оценки однородности совокупности – коэффициент вариации по факторным признакам
, совокупность однородна, если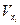 
≤ 33%
Линейный коэффициент корреляции
Несгруппированные данные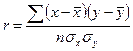 
Сгруппированные данные -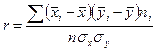 
Оценка существенности линейного коэффициента корреляции
при большом объеме выборки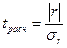 
, 
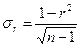. Если это отношение больше значения t-критерия Стьюдента (приложение 6, k=n-2, вероятность – 1-α)
при недостаточно большом объеме выборки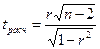 
, 
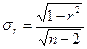
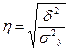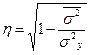Корреляционное отношение 
, 
, где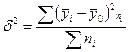 
, 
, 
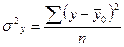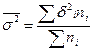
| Признаки | А(да) |  (нет)
| Итого |
| В (да) | a | b | a+b |
 (нет)
| c | d | c+d |
| Итого | a+c | b+d | n |
| A,b,c,d – частоты взаимного сочетания (комбинации) двух альтернативных признаков, n – общая сумма частот |
Коэффициент ассоциации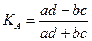 
Коэффициент контингенции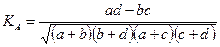 
Уравнение регрессии
Линейная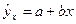 
Гиперболичская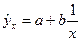 
Параболическая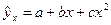 
Показательная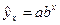 
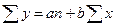
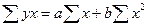
Для проверки возможности использования линейной функции определяется разность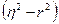 
, если она <0,1 то можно применить линейную функцию.
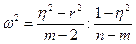, m – число групп. Если 
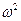< F-критерия, то можно. (Значение F-критерия определяется по таблице (приложение 5) α=0,05, число степеней свободы числителя (k1 = m-2) и знаменателя (k2 =n-m))
Достоверность уравнения корреляционной зависимости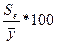 
, 
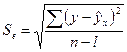- средняя квадратическая ошибка, y – фактические значения результативного признака, 
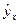- значения результативного признака, рассчитанные по уравнению регрессии, l – число параметров в уравнении регрессии.
Если это отношение не превышает 10-15%, то уравнение хорошо отображает изучаемую взаимосвязь.
Ряды динамики
Показатели динамики
| Показатель | Метод расчета | |
| С переменной базой (цепные) | С постоянной базой (базисные) | |
| Абсолютный прирост (показывает, на сколько в абсолютном выражении уровень текущего периода больше (меньше) базисного) |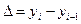 
| 
|
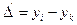
| Коэффициент роста (показывает, во сколько раз уровень текущего периода больше (меньше) базисного) |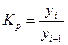 
| 
|
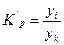
| Темп роста, % (это коэффициент роста, выраженный в %, показывает, сколько процентов уровень текущего периода составляет по отношению к уровню базисного периоа) |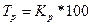 
| 
|
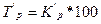
| Темп прироста, % (показывает, на сколько % уровень текущего периода больше (меньше) уровня базисного периода) |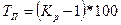 
| 
|
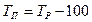
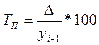
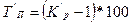
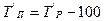
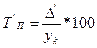
| Абсолютное значение 1% прироста (показывает, какая абсолютная величина скрывается за относительным показателем – одним процентом прироста) |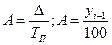 
| 
|
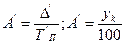
