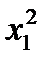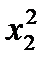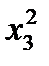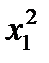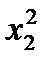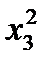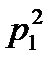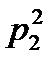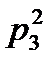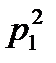Часть 1
Случайные события и их вероятности
1. Несколько событий называются ____________, если в результате испытания обязательно должно произойти одно из них.
| 1) | Несовместными | 4) | Равновозможными |
| 2) | Совместными | ||
| 3) | Противоположными |
2. События называются ____________, если наступление одного из них исключает появление любого другого.
| 1) | Несовместными | 4) | Равновозможными |
| 2) | Совместными | ||
| 3) | Противоположными |
3. Укажите вероятность невозможного события
| 1) | 1 | 2) | 0,9 | 3) | 0 | 4) | 0,01 |
4. Известно, что Р (А) = 0,65. Укажите вероятность противоположного события 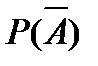
| 1) | 0,65 | 2) | 0,35 | 3) | 0,5 | 4) | -0,65 |
5. Три стрелка делают по одному выстрелу по мишени. Событие 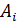 – попадание в мишень i -м стрелком. Событие
– попадание в мишень i -м стрелком. Событие  – промах i -м стрелком. Событие А – в мишень попали ровно два раза представляется в виде операций над событиями как…
– промах i -м стрелком. Событие А – в мишень попали ровно два раза представляется в виде операций над событиями как…
| 1) | 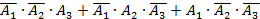
| 4) | 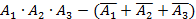
|
| 2) | 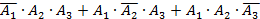
| ||
| 3) | 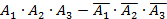
|
6. Равенство 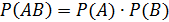 имеет место для __________ событий
имеет место для __________ событий
| 1) | Произвольных | 4) | Независимых |
| 2) | Несовместных | 5) | Зависимых |
| 3) | Совместных | 6) | Равновозможных |
7. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,9 и 0,4 соответственно. Вероятность того, что в цель попадут оба стрелка, равна
| 1) | 0,5 | 2) | 0,4 | 3) | 0,45 | 4) | 0,36 | ||||
| 1) | 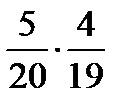
| 2) | 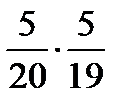
| 3) | 
| 4) | 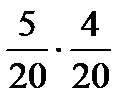
| ||||
8. В первом ящике 7 красных и 9 синих шаров, во втором – 4 красных и 11 синих. Из произвольного ящика достают один шар. Вероятность того, что он красный равна …
| 1) | 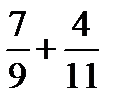
| 2) | 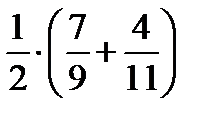
| 3) | 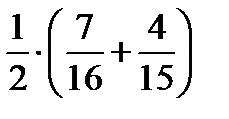
| 4) | 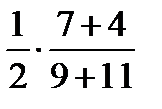
|
9. Формула Байеса имеет вид …
| 1) | 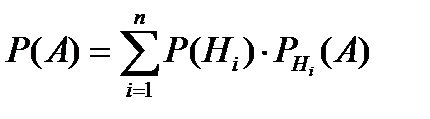
| 2) | 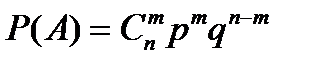
|
| 3) | 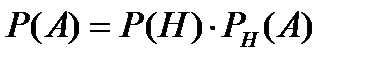
| 4) | 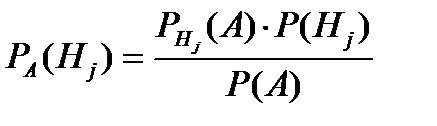
|
10. Вероятность рождения мальчика равна 0,51. В семье 5 детей. Вероятность того, что среди них ровно 2 мальчика равна…
| 1) | 
| 4) | 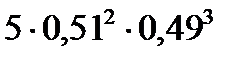
|
| 2) | 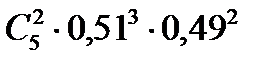
| 5) | 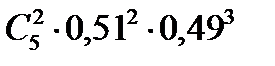
|
| 3) | 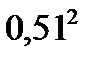
| 6) | 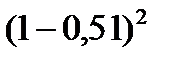
|
11. Монету подбросили 100 раз. Для определения вероятности того, что событие А – появление герба – наступит не менее 60 раз и не более 80 раз, целесообразно воспользоваться…
| А) | Формулой полной вероятности |
| В) | Формулой Байеса |
| С) | Формулой Пуассона |
| D) | Локальной теоремой Муавра-Лапласа |
Часть 2
Случайные величины и законы их распределений
12. Задан ряд распределения случайной величины Х:
| Х | -1 | ||
| P | 0,1 | ? | 0,3 |
Значение 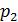 равно …0,6
равно …0,6
13. Случайная величина Х задана законом распределения
| Х | 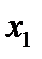
| 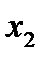
| 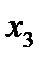
|
| P | 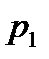
| 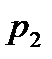
| 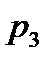
|
Ряд распределения случайной величины 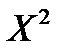 имеет вид
имеет вид
| 1) |
| 3) |
| ||||||||||||||||
| 2) |
| 4) |
|
14. Дискретная случайная величина Х задана законом распределения вероятностей
| Х | |||
| Р | 0,4 | 0,1 | 0,5 |
Математическое ожидание M (X) равно…
| 1) | 4,67 | 2) | 3 | 3) | 7 | 4) | 5,1 |
15. Математическое ожидание дискретной случайной величины рассчитывается по формуле …
| 1) | 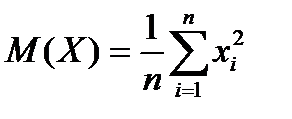
| 2) | 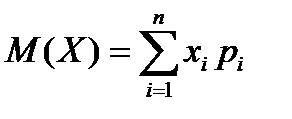
| 3) | 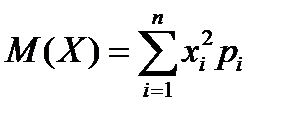
| 4) | 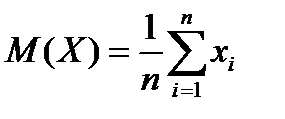
|
16. Пусть Х – дискретная случайная величина, заданная законом распределения вероятностей:
| Х | -1 | |
| Р | 0,4 | 0,6 |
Тогда дисперсия этой случайной величины равна …
| 1) | 15,4 | 2) | 8,64 | 3) | 2,6 | 4) | 2,93 |
17. Укажите все формулы, по которым можно рассчитать дисперсию дискретной случайной величины
| 1) | 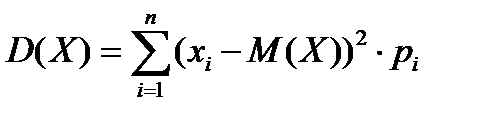
| 2) | 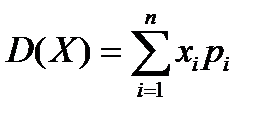
|
| 3) | 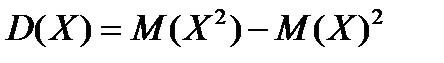
| 4) | 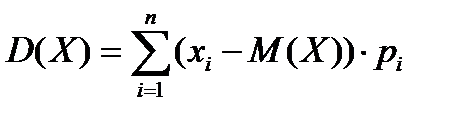
|
| 5) | 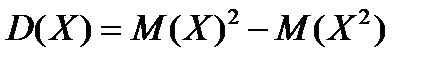
|
Интегральная и дифференциальная функции распределения случайной величины
18. Функция распределения непрерывной случайной величины имеет вид
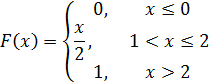
Плотность вероятности этой случайной величины на промежутке 1 < х ≤ 2 равна …1/2
19. Случайная величина задана плотностью распределения 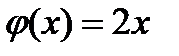 в интервале (0;1); вне этого интервала
в интервале (0;1); вне этого интервала 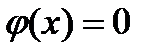 . Вероятность
. Вероятность 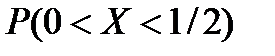 равна …1/4
равна …1/4
20. Случайная величина задана плотностью распределения 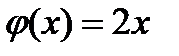 в интервале (0;1); вне этого интервала
в интервале (0;1); вне этого интервала 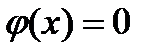 . Математическое ожидание величины X равно …
. Математическое ожидание величины X равно …
| 1) | 1/2 | 2) | 1 | 3) | 4/3 | 4) | 2/3 |
21. Случайная величина задана плотностью распределения 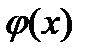 в интервале (0;1); вне этого интервала
в интервале (0;1); вне этого интервала 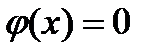 . Математическое ожидание величины X равно …
. Математическое ожидание величины X равно …
| 1) | 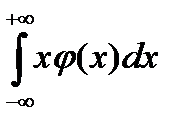
| 2) | 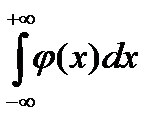
| 3) | 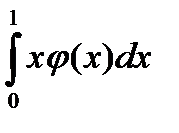
| 4) | 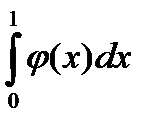
|
22. Дисперсия непрерывной случайной величины может быть рассчитана по формуле
| 1) | 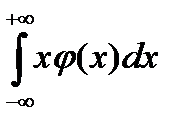
| 2) | 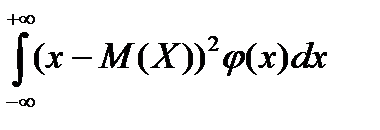
| 3) | 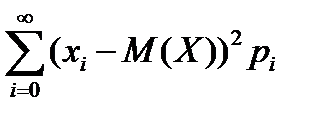
| 4) | 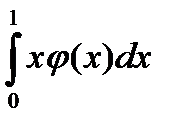
|
23. Плотность вероятности нормально распределенной случайной величины Х при 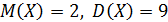 , имеет вид:
, имеет вид:
| 1) | 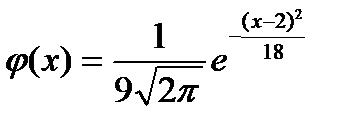
| 2) | 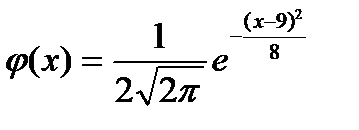
|
| 3) | 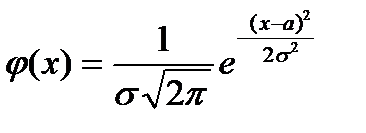
| 4) | 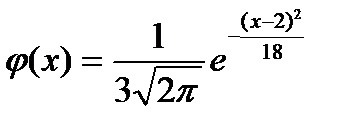
|
Часть 3
Элементы математической статистики
24. Из генеральной совокупности извлечена выборка объема 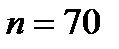 , полигон частот которой имеет вид
, полигон частот которой имеет вид
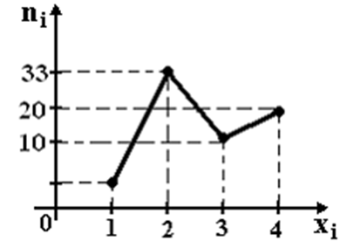
Тогда число вариант 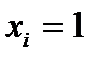 в выборке равно …
в выборке равно …
| 1) | 8 | 2) | 7 | 3) | 70 | 4) | 6 |
25. Объем выборки 1, 2, 2, 2, 3, 3, 4, 4, 6 равен …9
26. Мода вариационного ряда, полученного по выборке 1, 2, 2, 2, 3, 4, 4, 6 равна …2
27. Размах вариационного ряда, полученного по выборке 1, 2, 2, 2, 3, 4, 4, 6 равен …5
28. Дан вариационный ряд
| варианта | ||||
| частота |
Медиана этого ряда равна …7
29. Математическое ожидание оценки 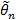 параметра
параметра 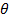 равно оцениваемому параметру. Оценка
равно оцениваемому параметру. Оценка 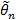 является
является
| 1) | Смещенной | 2) | Состоятельной |
| 3) | Несмещенной | 4) | Эффективной |
30. Оценка 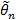 параметра
параметра 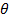 сходится по вероятности к оцениваемому параметру. Оценка
сходится по вероятности к оцениваемому параметру. Оценка 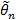 является
является
| 1) | Смещенной | 2) | Состоятельной |
| 3) | Несмещенной | 4) | Эффективной |
31. Произведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 8, 8. Тогда несмещенная оценка математического ожидания равна …
| 1) | 5 | 2) | 6 | 3) | 5,5 | 4) | 5,25 |
32. Выборочная дисперсия вариационного ряда равна 3,5. Объем выборки равен 50. Исправленная выборочная дисперсия равна …
| 1) | 3,43 | 2) | 3,57 | 3) | 0,07 | 4) | 3,5 |
33. Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид…
| 1) | (10,5; 11,5) | 2) | (11; 11,5) | 3) | (10,5; 10,9) | 4) | (10,5; 11) |
34. Дана выборка объема n. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее 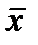 …
…
| 1) | Не изменится | 2) | Увеличится в 25 раз |
| 3) | Уменьшится в 5 раз | 4) | Увеличится в 5 раз |
35. Дан вариационный ряд
| варианта | |||
| частота |
Выборочная дисперсия равна …
| 1) | 4 | 2) | 1,8 | 3) | 0,84 | 4) | 0,76 |
36. Дан вариационный ряд
| варианта | |||
| частота |
Исправленная выборочная дисперсия равна …
| 1) | 4 | 2) | 1,8 | 3) | 0,84 | 4) | 0,76 |
37. Если основная гипотеза имеет вид 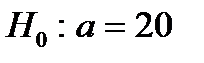 , то конкурирующей гипотезой может быть гипотеза …
, то конкурирующей гипотезой может быть гипотеза …
| 1) | 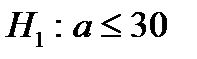
| 2) | 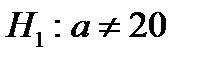
| 3) | 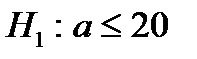
| 4) | 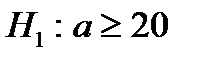
|
38. Если основная гипотеза имеет вид 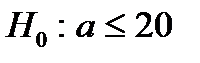 , то конкурирующей гипотезой может быть гипотеза …
, то конкурирующей гипотезой может быть гипотеза …
| 1) | 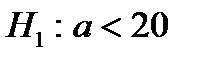
| 2) | 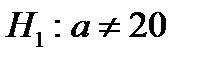
| 3) | 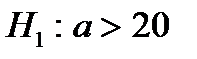
| 4) | 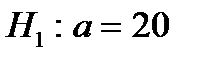
|