Построим ряд распределения предприятий по величине собственных оборотных средств на основании таблицы 1.2 (табл. 2.1).
Таблица 2.1
Распределение 50 предприятий по величине собственных оборотных средств
| Собственные оборотные средства, тыс.руб. | Количество предприятий (частота) | В % в итогу | Накопленное количество предприятий |
| 320-736 | |||
| 736-1152 | |||
| 1152-1568 | |||
| 1568-1984 | |||
| 1984-2400 | |||
Изобразим этот ряд графически в виде гистограммы распределения, состоящей из столбиков с основаниями, равными ширине интервалов и высотой, соответствующей количеству предприятий. Соединив середины верхних граней столбиков, получим полигон распределения (см. рис. 2.1)
Рис. 2.1
Гистограмма распределения 50 предприятий по величине собственных оборотных средств
Построим кумуляту распределения предприятий по величине собственных оборотных средств, отложив по горизонтальной оси значения варианты, а по вертикальной – накопленные частоты (см. рис. 2.2)
Рис.2.2
Кумулята распределения 50 предприятий по величине собственных оборотных средств
Рассчитаем среднюю величину собственных оборотных средств, взяв за значения осредняемого признака середины интервалов, и произведем расчет по средней арифметической взвешенной (таблица 2.2)
Таблица 2.2
Расчет средней величины собственных оборотных средств
| Собственные оборотные средства, тыс.руб. | Середина интервала, x’ | Количество предприятий, fi | x’∙fi |
| 320-736 | |||
| 736-1152 | |||
| 1152-1568 | |||
| 1568-1984 | |||
| 1984-2400 | |||
| Всего |

Итак, средняя величина собственных оборотных средств для данных предприятий составляет 919,04 тыс.руб.
Рассчитаем структурные средние – моду и медиану.
Модальным интервалом будет интервал от 736 до 1152 тыс.руб., т.к. частота этого интервала наибольшая. Вычислим моду по формуле:

где xMo – нижняя граница модального интервала, ΔМо – ширина модального интервала; fMo, fMo-1 и fMo+1 – частоты соответственно модального интервала, интервала, предшествующего модальному, и интервала, следующего за модальным.
В данном случае:

Итак, большинство данных предприятий имеют собственные оборотные средства около 775,62 тыс.руб.
Этот же интервал будет медианным, т.к. половина единиц совокупности (25) достигла значения внутри этого интервала. Вычислим медиану по формуле:
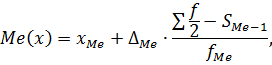
где хМе – нижняя граница медианного интервала, ΔМе – ширина медианного интервала, ΣfМе-1 – накопленная частота до медианного интервала, fMе – частота медианного интервала. В данном случае:

Итак, половина данных предприятий имеют собственные оборотные средства меньше 830,55 тыс.руб., а половина – больше.
Для расчета показателей вариации составим таблицу 2.3.
Таблица 2.3
Расчет показателей вариации собственных оборотных средств
| Группы предприятий по величине собственных оборотных средств, тыс.руб. | Число предприятий в группе, fi | Середина интервала, хi | xi fi | xi - 
| (xi -  )2 )2
| (xi -  )2fi )2fi
|
| 320-736 | -391,04 | |||||
| 736-1152 | 24,96 | |||||
| 1152-1568 | 440,96 | |||||
| 1568-1984 | 856,96 | |||||
| 1984-2400 | 1272,96 | |||||
| Итого | ___ | ____ | ____ |
Найдем дисперсию, среднеквадратичное отклонение и коэффициент вариации по формулам:


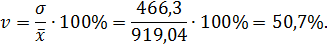
Итак, коэффициент вариации величины собственных оборотных средств равен 50,7%, что свидетельствует о большом разбросе значений данного признака и о том, что вычисленная средняя является нетипичной.
Перейдем ко второму признаку – дебиторской задолженности предприятий. Построим ряд распределения предприятий по величине дебиторской задолженности на основании таблицы 1.3 (табл. 2.4)
Таблица 2.4
Распределение 50 предприятий по величине дебиторской задолженности
| Дебиторская задолженность, тыс.руб. | Количество предприятий (частота) | В % к итогу | Накопленное количество предприятий |
| от 12 до 16,33 | |||
| от 16,33 до 20,66 | |||
| от 20,66 до 24,99 | |||
| от 24,99 до 29,32 | |||
| от 29,32 до 33,65 | |||
| от 33,65 до 38 | |||
Дадим графическое представление этого ряда в виде гистограммы распределения. Соединив середины верхних граней ее столбиков, получим полигон распределения (см. рис.2.3). На основе накопленной частоты построим кумуляту распределения (см. рис.2.4).
Рис. 2.3
Гистограмма распределения 50 предприятий по величине дебиторской задолженности
Рис. 2.4
Кумулята распределения 50 предприятий по величине дебиторской задолженности
Рассчитаем среднюю величину дебиторской задолженности (таблица 2.5).
Таблица 2.5
Расчет средней величины дебиторской задолженности
| Дебиторская задолженность, тыс.руб. | Середина интервала, x’ | Количество предприятий, fi | x’∙fi |
| 12-16,33 | 14,17 | 198,33 | |
| 16,33-20,66 | 18,5 | 55,50 | |
| 20,66-24,99 | 22,83 | 182,67 | |
| 24,99-29,32 | 27,16 | 380,33 | |
| 29,32-33,65 | 31,49 | 126,00 | |
| 33,65-38 | 35,83 | 250,83 | |
| 1193,67 |

Итак, средняя величина дебиторской задолженности для данных предприятий составляет 23,87 тыс.руб.
Рассчитаем моду и медиану.
Мы имеем два интервала с наибольшей частотой – от 12 до 16,33 тыс.руб. и от 24,99 до 29,32 тыс.руб. Считая модальным первый интервал, получим значение моды:

Считая модальным второй интервал, получаем другое значение моды:
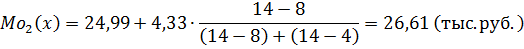
Итак, большинство предприятий имеют дебиторскую задолженность около 14,42 тыс.руб. и около 26,61 тыс.руб.
Медианным интервалом будет интервал от 24,99 до 29,32 тыс.руб., т.к. в этом интервале накопленная частота достигает половины общего числа предприятий. Вычислим медиану:

Итак, половина предприятий имеет дебиторскую задолженность меньше 24,99 тыс.руб., а половина – больше.
Для расчета показателей вариации составим таблицу 2.6.
Таблица 2.6
Расчет показателей вариации величины дебиторской задолженности
| Группы предприятий по величине дебиторской задолженности, тыс.руб. | Число предприятий в группе, fi | Середина интервала, хi | xi fi | xi - 
| (xi -  )2 )2
| (xi -  )2fi )2fi
|
| 12-16,33 | 14,17 | 198,33 | -9,71 | 94,22 | 1319,07 | |
| 16,33-20,66 | 18,5 | 55,50 | -5,37 | 28,87 | 86,62 | |
| 20,66-24,99 | 22,83 | 182,67 | -1,04 | 1,08 | 8,65 | |
| 24,99-29,32 | 27,16 | 380,33 | 3,29 | 10,85 | 151,84 | |
| 29,32-33,65 | 31,49 | 126,00 | 7,63 | 58,17 | 232,66 | |
| 33,65-38 | 35,82 | 250,83 | 11,96 | 143,04 | 1001,29 | |
| Итого | _____ | 1193,67 | ____ | ____ | 2800,14 |
Найдем дисперсию, среднеквадратичное отклонение и коэффициент вариации:



Итак, коэффициент вариации дебиторской задолженности предприятий равен 31,3%, что свидетельствует о не очень большом разбросе значений, поэтому найденная средняя является достаточно типичной.
Выборочное исследование
Допустим, что вся информация о величине собственных оборотных средств получена при помощи 10%-ного собственно случайного бесповторного отбора. Тогда данная совокупность является выборочной совокупностью с объемом n=50 предприятий, а объем генеральной совокупности N=500 предприятий. Значение средней 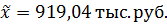 , вычисленное в задании 2, является выборочной средней. Найдем пределы, за которые с достоверностью 95,4% не выйдет среднее значение по всей генеральной совокупности.
, вычисленное в задании 2, является выборочной средней. Найдем пределы, за которые с достоверностью 95,4% не выйдет среднее значение по всей генеральной совокупности.
Найдем среднюю ошибку выборки, которая в случае бесповторного отбора вычисляется по формуле

где  - дисперсия признака в выборочной совокупности, которую подставим из задания 2:
- дисперсия признака в выборочной совокупности, которую подставим из задания 2:

На основании средней ошибки вычисляется предельная ошибка выборки Δ=tμ, где t – коэффициент доверия, зависящий от вероятности, с которой необходимо найти среднее значение признака по генеральной совокупности. При вероятности 0,954 t=2, поэтому предельная ошибка будет равна
Δ=2∙62,56=125,12 (тыс.руб.)
Тогда получаем границы изменения генеральной средней:
 – Δ ≤
– Δ ≤ 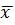

 + Δ;
+ Δ;
919,04–125,12 ≤ 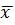
 919,04+125,12;
919,04+125,12;
793,92 ≤ 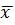
 1044,16.
1044,16.
Найдем, какое количество предприятий необходимо обследовать для того, чтобы снизить предельную ошибку выборки на 50%. Новая ошибка будет равна Δ’ = 0,5Δ = 62,56 тыс.руб., а новая выборочная совокупность будет содержать количество предприятий, которое для бесповторного отбора находится по формуле:

В данном случае:

Итак, среднее значение величины собственных оборотных средств по всей генеральной совокупности с вероятностью 0,954 лежит в интервале от 793,92 до 1044,16 тыс.руб. Чтобы снизить предельную ошибку выборки на 50%, необходимо увеличить объем выборочной совокупности до 154 предприятий.
Допустим, что информация о величине дебиторской задолженности получена при помощи 10%-ного повторного отбора. Объемы выборочной и генеральной совокупности по-прежнему равны n=50 и N=500.
Определим долю предприятий, значения дебиторской задолженности которых выше медианного. В выборочной совокупности медианным интервалом является интервал от 24,99 до 29,32 тыс.руб., и выше этого интервала лежат 11 предприятий, или 22%, поэтому выборочная доля w=0,22.
Средняя ошибка выборки для повторного отбора рассчитывается по формуле  где
где  – дисперсия доли. В данном случае
– дисперсия доли. В данном случае  .
.
Тогда предельная ошибка выборки с достоверностью 0,954, которой соответствует коэффициент доверия t=2, будет равна Δ=2∙0,06=0,12.
Пределы, в которых лежит значение генеральной доли р с данной достоверностью, составят:
w – Δ ≤ p ≤ w + Δ;
0,22 – 0,12 ≤ р ≤ 0,22 + 0,12;
0,1 ≤ р ≤ 0,34.
Найдем, какое количество предприятий необходимо обследовать, чтобы снизить предельную ошибку на 20%. Новая предельная ошибка будет равна Δ’ = 0,8Δ = 0,094, а необходимое количество предприятий при повторном отборе находится по формуле 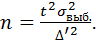
В данном случае: 
Итак, доля предприятий со значениями дебиторской задолженности выше медианного с вероятностью 0,954 лежит в интервале от 0,1 до 0,34. Чтобы снизить предельную ошибку выборки на 20%, необходимо увеличить объем выборочной совокупности до 78 предприятий.
Индексы
В таблице 4.1 представлены данные о выпуске предприятием продукции трех видов А, В и С за 2008 г. (базисный период) и 2009 г. (отчетный период). Через p0 и р1 обозначены цены за единицу продукции в базисном и отчетном периоде соответственно, а через q0 и q1 – физический объем продукции в тех же периодах.
Таблица 4.1
Данные о выпуске продукции по видам и ценам за 2008 и 2009 г.
| Вид продукции | 2008 г. | 2009 г. | ||||||
| qo | p0 | p0q0 | p1q0 | q1 | p1 | p1q1 | p0q1 | |
| А | ||||||||
| В | ||||||||
| С | ||||||||
| Итого | ___ | ____ | ___ | ___ |
Определим индивидуальные индексы физического объема, цены и стоимости по каждому из трех видов продукции и проверим их взаимосвязь.
По продукции А:


По продукции В:
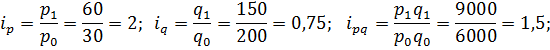

По продукции С:

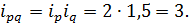
Определим общие индексы физического объема и цены по методам Ласпейреса и Пааше, а также общий индекс стоимости, и проверим их взаимосвязь:
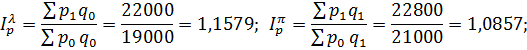
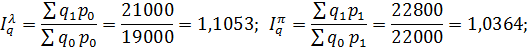


Результаты вычислений занесем в таблицу 4.2.
Таблица 4.2
Индексы физического объема, цены и стоимости
| Индексы | Вид продукции | Общий | ||
| А | В | С | ||
| Цены | 0,4 | 1,0857 | ||
| Физического объема | 1,2 | 0,75 | 1,5 | 1,1053 |
| Стоимости | 0,48 | 1,5 | 1,2 |
Итак, в 2009 г. объем товарооборота на исследуемом предприятии увеличился на 20%, что произошло в результате увеличения стоимости продукции В на 50% и продукции С в 3 раза, тогда как стоимость продукции А упала на 52%. За счет изменения цен товарооборот увеличился на 8,57%, что произошло в результате увеличения цен на продукцию В и С в 2 раза, при этом цена продукции А упала на 60%. За счет изменения физического объема товарооборот увеличился на 10,53%, что произошло в результате увеличения физического объема продукции А на 20%, а продукции С на 50% при одновременном уменьшении объема продукции В на 25%.
Определим абсолютное изменение стоимости продукции и выявим, на сколько она изменилась в результате изменения цен и в результате изменения физического объема:



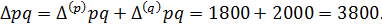
Итак, стоимость продукции в текущем периоде по сравнению с базисным увеличилась на 3800 денежных единиц, в том числе на 1800 денежных единиц за счет изменения цен и на 2000 денежных единиц за счет изменения физического объема.
Считая всю продукцию однородной, определим индекс средней цены и проанализируем влияние изменения цен на отдельные виды продукции и ассортиментных (структурных) сдвигов:

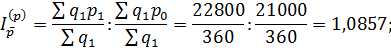

Итак, средняя цена продукции данного предприятия увеличилась по сравнению с базисным периодом на 20%. При этом за счет изменения цен на отдельные виды продукции средняя цена увеличилась на 8,57%, а за счет структурных сдвигов – на 10,53%.
Ряды динамики
В таблице 5.1 приведены данные о фонде заработной платы на предприятии за период с 1999 по 2009 год.
Таблица 5.1
Фонд заработной платы на предприятии
| Годы | Фонд заработной платы, тыс.руб. |
Рассчитаем цепные и базисные показатели динамики по формулам:
– абсолютное изменение: Δц = уn – yn-1, Δб = yn – y0;
– коэффициенты роста: 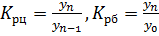 ;
;
– коэффициенты прироста: Кпр = Кр – 1;
– темпы роста и темпы прироста: Тр = Кр ∙ 100%, Тпр = Кпр ∙ 100%,
где уn – значение показателя в текущем периоде, yn-1 – в предыдущем периоде, а y0 – в базисном (первом) периоде.
Результаты занесены в таблицу 5.2.
Таблица 5.2
Цепные и базисные показатели динамики фонда заработной платы
| Годы | Фонд заработной платы, тыс.руб. | Абсолютное изменение | Коэффициенты роста | Коэффициенты прироста | Темпы роста | Темпы прироста | |||||
| цепные | базисные | цепные | базисные | цепные | базисные | цепные | базисные | цепные | базисные | ||
| ____ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ||
| 1,0327 | 1,0327 | 0,0327 | 0,0327 | 103,27 | 103,27 | 3,27 | 3,27 | ||||
| 1,0800 | 1,1153 | 0,0800 | 0,1153 | 108,00 | 111,53 | 8,00 | 11,53 | ||||
| 1,0448 | 1,1652 | 0,0448 | 0,1652 | 104,48 | 116,52 | 4,48 | 16,52 | ||||
| 1,1049 | 1,2874 | 0,1049 | 0,2874 | 110,49 | 128,74 | 10,49 | 28,74 | ||||
| 1,0695 | 1,3769 | 0,0695 | 0,3769 | 106,95 | 137,69 | 6,95 | 37,69 | ||||
| 1,0125 | 1,3941 | 0,0125 | 0,3941 | 101,25 | 139,41 | 1,25 | 39,41 | ||||
| 1,1123 | 1,5508 | 0,1123 | 0,5508 | 111,23 | 155,08 | 11,23 | 55,08 | ||||
| 1,0511 | 1,6299 | 0,0511 | 0,6299 | 105,11 | 162,99 | 5,11 | 62,99 | ||||
| 1,3105 | 2,1360 | 0,3105 | 1,1360 | 131,05 | 213,60 | 31,05 | 113,60 | ||||
| 1,1749 | 2,5095 | 0,1749 | 1,5095 | 117,49 | 250,95 | 17,49 | 150,95 |
Из таблицы видно, что на протяжении всего рассматриваемого периода фонд заработной платы на предприятии увеличивался. Наибольшее абсолютное изменение фонда заработной платы наблюдалось в 2008 г., когда данный показатель увеличился на 294 тыс.руб. по сравнению с предыдущим годом. В этом же году наблюдался наибольший темп прироста фонда заработной платы (31,05%). Наименьший рост наблюдался в 2005 г. (фонд заработной платы по сравнению с предыдущим годом вырос всего на 10 тыс.руб., или на 1,25%).
Рассчитаем средние показатели ряда динамики.
Так как данный ряд динамики является интервальным, то средний уровень ряда можно вычислить по средней арифметической простой (n – число уровней ряда):

Среднее абсолютное изменение – это среднее арифметическое от абсолютных изменений за каждый год. Его можно вычислить следующим образом:

В этой формуле n – число приростов, т.е. число, на единицу меньшее общего количества уровней ряда.
Средний коэффициент роста – это среднее геометрическое из цепных коэффициентов роста за отдельные периоды времени динамического ряда. Используя связь между цепными и базисными показателями, его можно вычислить следующим образом:
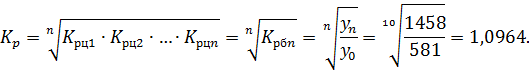
Здесь n – также число, на единицу меньшее общего количества уровней ряда (число коэффициентов роста).
Используя взаимосвязи между коэффициентами и темпами роста и прироста, находим эти средние показатели:
Тр = Кр ∙ 100% = 109,64%; Кпр = Кр – 1 = 0,0964; Тпр = Кпр ∙ 100% =9,64%.
Итак, средний уровень фонда заработной платы за рассматриваемые годы составил 855,55 тыс.руб. В среднем за каждый год фонд заработной платы увеличивался на 87,7 тыс.руб. Средний темп прироста фонда заработной платы в год составил 9,64%.
Произведем сглаживание ряда динамики методом трехлетней скользящей средней. Сглаженные уровни ряда будут равняться:


и т.д.
Произведем также аналитическое выравнивание ряда динамики по формуле  , где
, где  – расчетные значения уровней ряда, а t – время, которое для удобства принимает значения –5, –4, …, 4, 5 (при этом средний уровень ряда соответствует t=0 и сумма всех значений t также равна нулю). Для расчета коэффициентов а0 и а1 составим таблицу 5.3, куда занесем также сглаженные уровни ряда методом скользящей средней.
– расчетные значения уровней ряда, а t – время, которое для удобства принимает значения –5, –4, …, 4, 5 (при этом средний уровень ряда соответствует t=0 и сумма всех значений t также равна нулю). Для расчета коэффициентов а0 и а1 составим таблицу 5.3, куда занесем также сглаженные уровни ряда методом скользящей средней.
Таблица 5.3
Сглаживание и аналитическое выравнивание ряда динамики
| Годы | Фонд заработной платы, тыс.руб. | Сглаженные уровни | Условное обозначение времени | Квадрат | Произведение | Расчетные значения |
| Символы | y | ___ | t | t2 | yt | 
|
| ___ | –5 | –2905 | 475,73 | |||
| 609,7 | –4 | –2400 | 551,69 | |||
| 641,7 | –3 | –1944 | 627,65 | |||
| 691,0 | –2 | –1354 | 703,62 | |||
| 741,7 | –1 | –748 | 779,58 | |||
| 786,0 | 855,55 | |||||
| 837,0 | 931,51 | |||||
| 886,0 | 1007,47 | |||||
| 1029,7 | 1083,44 | |||||
| 1215,3 | 1159,40 | |||||
| ___ | 1235,36 | |||||
| Итого | ___ |

Данные коэффициенты показывают, что средний уровень выровненного ряда динамики фонда заработной платы составляет 855,55 тыс.руб. Выровненные значения фонда заработной платы равномерно возрастают на 75,96 тыс.руб. в год.
Графически фактический и выровненный ряды показаны на рисунке 5.1.
Рис. 5.1
Фактические и выровненные уровни ряда динамики фонда заработной платы
Анализ взаимосвязи
Вернемся к данным о собственных оборотных средствах и дебиторской задолженности 50 предприятий, приведенным в таблице 1.1, над которыми выполнялись задания 1-3. Исследуем возможную взаимосвязь между этими двумя признаками.
Для выявления связи, определения ее направления и тесноты используется корреляционный анализ.
Сначала нужно установить наличие связи. Для этого проведем визуализацию связи, нарисовав поле корреляции (рис. 6.1).

Рис. 6.1
Поле корреляции между собственными оборотными средствами и дебиторской задолженностью предприятий
На поле корреляции точки, соответствующие отдельным предприятиям, расположены в общем достаточно хаотично: нет единой линии, вдоль которой выстраивается большинство точек. Можно представить себе линию со слабым положительным наклоном, такую, которая делила бы совокупность данных точек примерно пополам, но приближение такой линией будет иметь большую погрешность. Это значит, что между собственными оборотными средствами и дебиторской задолженностью предприятий можно выделить формальную слабую прямую связь, но фактически связь практически отсутствует.
Рассмотрим аналитическую группировку предприятий, проведенную в 1 задании (см. табл. 1.4). По ней также видно, что явной связи между данными признаками не выявляется, так как средняя величина дебиторской задолженности хоть и возрастает по группам по величине собственных оборотных средств, но незначительно.
Степень тесноты и направление связи можно определить с помощью правила сложения дисперсий: 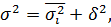
где  – общая дисперсия признака-результата, найденная в задании 2;
– общая дисперсия признака-результата, найденная в задании 2;
 – средняя из внутригрупповых дисперсий;
– средняя из внутригрупповых дисперсий;
 – межгрупповая дисперсия, вычисляемая по формуле
– межгрупповая дисперсия, вычисляемая по формуле
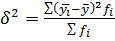 , где
, где  – среднее значение по группе,
– среднее значение по группе,  – общее среднее,
– общее среднее,  – число единиц в группе.
– число единиц в группе.
Найдем межгрупповую дисперсию на основании данных аналитической группировки (см. табл. 1.4) и вычисленного среднего значения дебиторской задолженности из задания 2:
 = [(23,25 – 23,87)2 ∙ 20 + (23,59 – 23,87)2 ∙ 22 + (23,67 – 23,87)2 ∙ 3 +
= [(23,25 – 23,87)2 ∙ 20 + (23,59 – 23,87)2 ∙ 22 + (23,67 – 23,87)2 ∙ 3 +
+ (24 – 23,87)2 ∙ 1 + (31 – 23,87)2 ∙ 4] / 50 = 4,257.
Найдем коэффициент детерминации

и эмпирическое корреляционное отношение

Низкое значение эмпирического корреляционного отношения показывает, что связь между данными двумя признаками практически отсутствует.
Проведем регрессию между данными двумя признаками на основании линейной зависимости 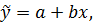 где х – значения признака-фактора (собственных оборотных средств), у – значения признака-результата (дебиторской задолженности),
где х – значения признака-фактора (собственных оборотных средств), у – значения признака-результата (дебиторской задолженности),  – расчетные значения результативного признака. Данные для расчетов приведены в таблице 6.1.
– расчетные значения результативного признака. Данные для расчетов приведены в таблице 6.1.
Таблица 6.1
Расчеты для линейной регрессии
| № п/п | х | у | х2 | ху | у2 | 
|
| 22,204 | ||||||
| 23,176 | ||||||
| 23,889 | ||||||
| 22,723 | ||||||
| 24,635 | ||||||
| 22,787 | ||||||
| 22,820 | ||||||
| 22,852 | ||||||
| 22,528 | ||||||
| 22,496 | ||||||
| 23,711 | ||||||
| 25,218 | ||||||
| 24,375 | ||||||
| 23,889 | ||||||
| 23,598 | ||||||
| 24,213 | ||||||
| 27,649 | ||||||
| 23,241 | ||||||
| 23,517 | ||||||
| 22,982 | ||||||
| 23,565 | ||||||
| 24,181 | ||||||
| 22,771 | ||||||
| 22,447 | ||||||
| 24,343 | ||||||
| 23,970 | ||||||
| 28,945 | ||||||
| 24,991 | ||||||
| 22,755 | ||||||
| 23,137 | ||||||
| 24,278 | ||||||
| 22,415 | ||||||
| 24,505 | ||||||
| 23,338 | ||||||
| 23,938 | ||||||
| 24,311 | ||||||
| 28,313 | ||||||
| 25,947 | ||||||
| 27,513 | ||||||
| 23,727 | ||||||
| 24,246 | ||||||
| 22,382 | ||||||
| 23,241 | ||||||
| 23,750 | ||||||
| 24,239 | ||||||
| 24,489 | ||||||
| 23,718 | ||||||
| 23,082 | ||||||
| 23,880 | ||||||
| 28,077 | ||||||
| Всего | ||||||
| Среднее | 892,66 | 24,06 | 1030707,18 | 22235,38 | 637,34 | 24,06 |
Значения параметров a и b найдены по следующим формулам:

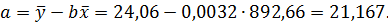
Видно, что расчетные значения дебиторской задолженности сильно отличаются от фактических, что свидетельствует о том, что выраженная линейная связь между данными двумя признаками отсутствует.
Найдем коэффициент корреляции:
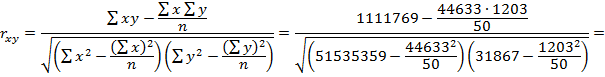
= 0,205.
Итак, различными методами было обнаружено, что связь между величиной собственных оборотных средств и дебиторской задолженностью очень слабая, практически отсутствует.






