С помощью χ2-критерия проверить, случайно ли данное распределение. Рассчитайте коэффициенты Пирсона и Чупрова, сделайте выводы

Тема 7: Корреляционно-регрессионный анализ.

Для расчета параметров уравнения регрессии a₀ и а₁ (а₂) (в основном используется линейное уравнение регрессии - для парной регрессии и - для множественной регресии с двумя факторными признаками) применятся метод наименьших квадратов, решая систему нормальных уравнений для парной регрессии:

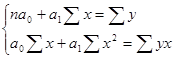
для множественной регрессии:

;

;

;

В уравнениях регрессии параметр а ₀ показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр а _i показывает, насколько изменяется в среднем значение результативного признака при изменении i-ого факторного на единицу его собственного измерения.

Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии. Значимость коэффициента регрессии осуществляется с помощью средней ошибки каждого параметраа_i – μ_{a i.}

где σ²_ост – остаточная дисперсия

Сопоставляя значение параметра с его средней ошибкой, по значению судят о значимости данного параметра. Если число наблюдений п>20, то параметр считается значимым при t>3. Если п<20, то обращаются к специальным таблицам значений t-критерия Стьюдента (см. Приложение 5). И в данном случае параметр считается значимым при (a; v=n-k-1), где a - уровень значимости, v=n-k-1 – число степеней свободы, k – число факторных признаков в уравнении.

где σ²_y - дисперсия результативного признака;

Адекватность полученной модели можно оценить с помощью средней ошибки аппроксимации: . Ее значение не должно превышать 12 – 15%, в противном случае модель считается неадекватной.

 

Пример.

Имеются следующие данные по 8 заводам о стоимости основных фондов, х (млн.руб.) и суточная выработка продукции у (тыс.т.):

х	3,0	3,3	3,5	3,7	3,7	4,5	4,5	4,9
у	9,1	10,2	10,0	10,5	10,3	12,9	12,8	13,1

Найти уравнение регрессии у по х; оценить адекватность модели с помощью средней ошибки аппроксимации; измерить тесноту зависимости между х и у с помощью коэффициента Фихнера, корреляционного отношения, коэффициента детерминации, линейного коэффициента корреляции, коэффициентов корреляции рангов Спирмена и Кендалла.

Решение:

Найдем уравнение регрессии, использовав уравнение прямой: .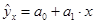

Параметры и можно определить при помощи системы нормальных уравнений, полученной по методу наименьших квадратов:

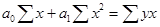
Промежуточные расчеты показателей представлены в таблице:

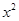
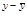
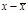
	х	у			ху						С/Н
1	3,0	9,1	9,00	82,81	27,3	9,08	0,02	0,002	-2,0	-0,9	С	4,00	0,00
2	3,3	10,2	10,89	104,04	33,66	9,77	0,43	0,044	-0,9	-0,6	С	0,81	0,18
3	3,5	10,0	12,25	100,00	35,00	10,23	-0,23	0,022	-1,1	-0,4	С	1,21	0,05
4	3,7	10,5	13,69	110,25	38,85	10,68	-0,18	0,017	-0,6	-0,2	С	0,36	0,03
5	3,7	10,3	13,69	106,09	38,11	10,68	-0,38	0,036	-0,8	-0,2	С	0,64	0,14
6	4,5	12,9	20,25	166,41	58,05	12,52	0,38	0,030	1,8	0,6	С	3,24	0,14
7	4,5	12,8	20,25	163,84	57,60	12,52	0,28	0,022	1,7	0,6	С	2,89	0,08
8	4,9	13,1	24,01	171,61	64,19	13,43	-0,33	0,025	2,0	1,0	С	4,00	0,11
	31,1	88,9	124,03	1005,05	352,76	88,9	-	0,198	-	-	-	17,15	0,73

Подставив полученные значения в систему уравнений, получим:

Решив систему уравнений, получим, что и , следовательно уравнение регрессии примет вид: .

Проверим полученное уравнение связи на адекватность при помощи средней ошибки аппроксимации: 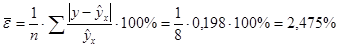(промежуточные расчеты смотри в таблице выше).

Так как полученная средняя ошибка аппроксимации 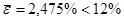, то модель можно считать адекватной, т.е. уравнение связи подобрано удачно.

Оценка тесноты связи измеряется различными способами:

· с помощью коэффициента Фихнера, основанного на количестве совпадений и несовпадений знаков отклонений индивидуальных значений факторного и результативного признаков от их средних значений:

,

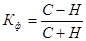где С – количество совпадений; Н – количество несовпадений.

· при линейной зависимости - с помощью линейного коэффициента корреляции.

или .

Линейный коэффициент корреляции изменяется в пределах от –1 до 1: - 1 < r < 1.

· при криволинейной зависимости измеряется с помощью эмпирического корреляционного отношения.

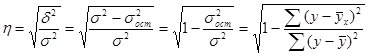
где 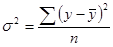- дисперсия результативного признака;

- факторная дисперсия.

· Коэффициент детерминации, определяемый по формуле: η² = δ² / σ², т.е. корреляционное отношение в квадрате характеризует долю вариации результативного признака, обусловленную изменчивостью изучаемого фактора.

· Для множественной регрессии тесноту связи можно оценить с помощью множественного коэффициента корреляции R. Если находится зависимость результативного признака только от двух факторных, то множественный коэффициент корреляции можно найти по формуле:

где - парные коэффициенты корреляции (тождественны линейному коэффициенту корреляции).

Наличие мультиколлинеарности признается, если парный коэффициент корреляции между факторными признаками > 0,8.

Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным.

a	b	a + b
c	d	c + d
a + c	b + d	a + b + c + d

Коэффициенты вычисляются по формулам:

ассоциации: ;

контингенции: .

Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если К_а > 0.5 или К_k > 0.3.

Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова, которые вычисляются по следующим формулам:

,

где j² – показатель взаимной сопряженности;

j² – определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки минус 1:

,

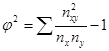где К₁ – число значений (групп) первого признака;

К₂ – число значений (групп) второго признака;

п_х , п_у - итоги по строкам и столбцам соответственно;

п_ху - значения признаков в ячейках таблицы.

Также коэффициенты Пирсона и Чупрова могут рассчитываться с использованием величины 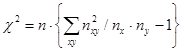, где n – число наблюдений.

; ,

 

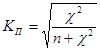Чем ближе величины К_П и К_Ч к 1, тем связь теснее.

Ранговые коэффициенты корреляции.

Коэффициент корреляции рангов ( коэффициент Спирмена ) рассчитывается по формуле (для случая, когда нет связных рангов):

,

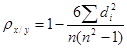где - квадраты разности рангов;

n – число наблюдений (число пар рангов).

При наличии связанных рангов расчеты производятся по следующим формулам:

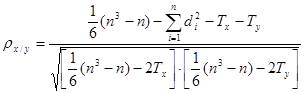
где , t_j – количество связных рангов.

Ранговый коэффициент корреляции Кендалла (τ) рассчитывается по формуле

,

где n – число наблюдений; S – сумма разностей между числом последовательностей и числом инверсий по второму признаку.

Расчет данного коэффициента выполняется в следующей последовательности:

1) значения х ранжируются в порядке возрастания или убывания, переставляются в том же порядке;

2) значения у располагаются в порядке, соответствующем значениям х;

3) для каждого ранга у определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяют величину Р как меру соответствия последовательностей рангов по х и у. Она учитывается со знаком «плюс»;

4) для каждого ранга у определяется число следующих за ним рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком «минус»;

5) определяется сумма баллов по всем членам ряда.

Если в изучаемой совокупности есть связанные ранги, то расчеты необходимо проводить по следующей формуле:

,

где .

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) W, который вычисляется по формуле:

,

где m – количество факторов; n – число наблюдений;

S – отклонение суммы квадратов рангов от средней квадратов рангов.

В случае наличия связанных рангов коэффициент конкордации определяется по формуле:

, где .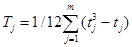

В большинстве случаев теснота связи может быть оценена по шкале тесноты связи:

 

Шкала тесноты связи

Значение коэффициентов корреляции	Характер связи
	Связь практически отсутствует
	Слабая связь
	Умеренная связь
	Сильная связь

 

Задача 88.

Имеются следующие данные по 8 заводам о стоимости основных производственных фондов, х (млн. руб.) и суточная выработка продукции у (тыс. т.):

х	3,0	3,3	3,5	3,7	3,7	4,5	4,5	4,9
у	9,1	10,2	10,0	10,5	10,3	12,9	12,8	13,1

Необходимо выполнить:

1) Найти уравнение регрессии у по х;

2) определить значимость его параметров; оценить адекватность модели с помощью средней ошибки аппроксимации;

3) измерить тесноту зависимости между х и у с помощью коэффициента Фихнера, теоретического корреляционного отношения, линейного коэффициента корреляции, коэффициентов корреляции рангов Спирмена и Кендалла.

4) Найти коэффициент эластичности; сделать выводы.

Задача 89.

За отчетный период имеются следующие данные о розничном товарообороте и издержках обращения по магазинам:

Магазин, № п/п	Объем розничного товарооборота, млн. руб.	Издержки обращения, млн. руб.
	20,1	1,62
	59,1	3,74
	82,5	4,66
	47,1	3,90
	24,5	1,51
	39,0	2,70
	51,1	3,09
	40,6	2,96
	64,2	4,47
	42,5	3,72

С помощью коэффициентов корреляции рангов Спирмена и Кендалла измерить тесноту связи между данными признаками.

Задача 90.

Имеются данные по 10 хозяйствам о количестве внесенных минеральных удобрений под зерновыми, х (кг/га) и об урожайности зерновых у (ц/га).

х
у	13,5	14,0	14,0	14,3	14,0	15,0	18,2	15,0	17,0	20,0

С помощью коэффициентов корреляции рангов Спирмена и Кендалла измерить тесноту связи между х и у.

Задача 91.

На основе опроса 400 работников коммерческих структур и 400 работников бюджетных организаций получено следующее их распределение по ответам на вопрос, довольны ли они своей заработной платой:

Работающие	Довольные з/п	Недовольные з/п	Итого
В коммерческих структурах
В бюджетных организациях
Итого работников

С помощью критерия Пирсона c² определить, случайно или нет данное распределение. Рассчитать коэффициенты ассоциации и контингенции.

Задача 92.

Имеются следующие данные о распределении 200 молочных ферм области по производительности труда и себестоимости молока:

Производительность   себестоимость	Высокая	Средняя	Низкая	Итого
Высокая
Средняя
Низкая
Итого

С помощью критерия c² проверить, случайно ли данное распределение, т.е. существует ли зависимость между производительностью труда и себестоимостью молока.

Измерить тесноту зависимости между показателями с помощью критериев взаимной сопряженности Пирсона и Чупрова.

Задача 93.

Распределение основных категорий потенциальных мигрантов по уровню образования представлено в таблице:

образование	Основные категории потенциальных мигрантов	Итого
Руководители	Специалисты	Служащие	Рабочие
Высшее
Неполное высшее
Среднее специальное
Среднее общее
Неполное среднее
итого

С помощью χ2-критерия проверить, случайно ли данное распределение. Рассчитайте коэффициенты Пирсона и Чупрова, сделайте выводы.