Формула Сімпсона
Якщо для кожної пари відрізків 
побудувати многочлен другого ступеня, потім про інтегрувати його і скористатися властивістю адитивності інтеграла, то одержимо формулу Сімпсона.
Розглянемо підінтегральну функцію f(x) на відрізку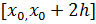 
. Замінимо цю підінтегральну функцію інтерполяційним многочлен Лагранжа другого ступеня, що збігає з f(x) у крапках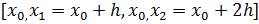 
Проінтегруємо: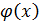 
: 
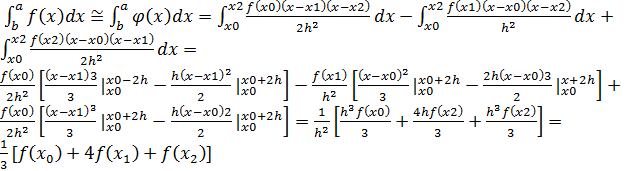
Формула: 
і називається формулою Сімпсона.
Отримане для інтеграла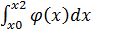 
значення збігається із площею криволінійної трапеції, обмеженою віссю 
, прямими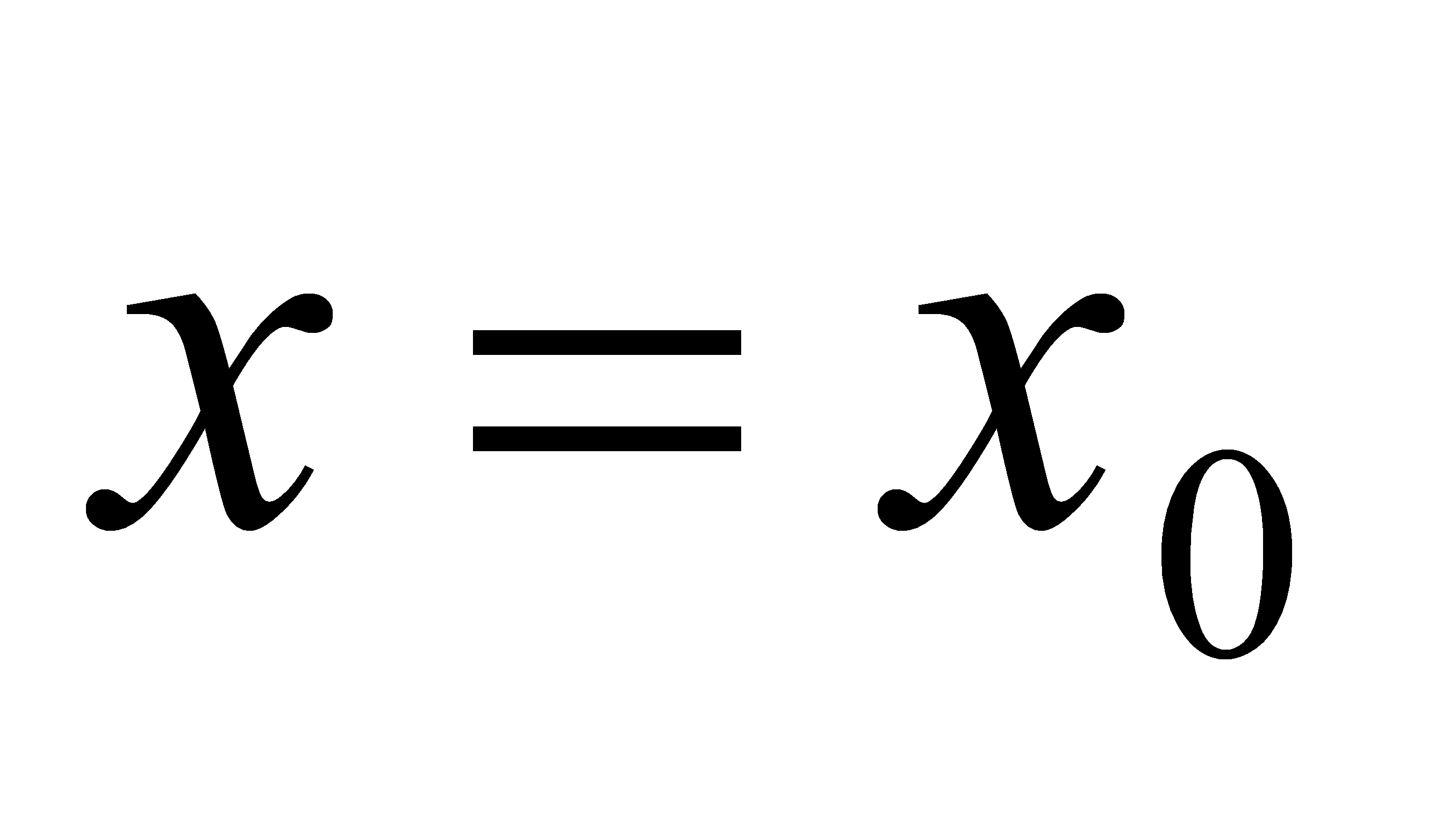 
, 
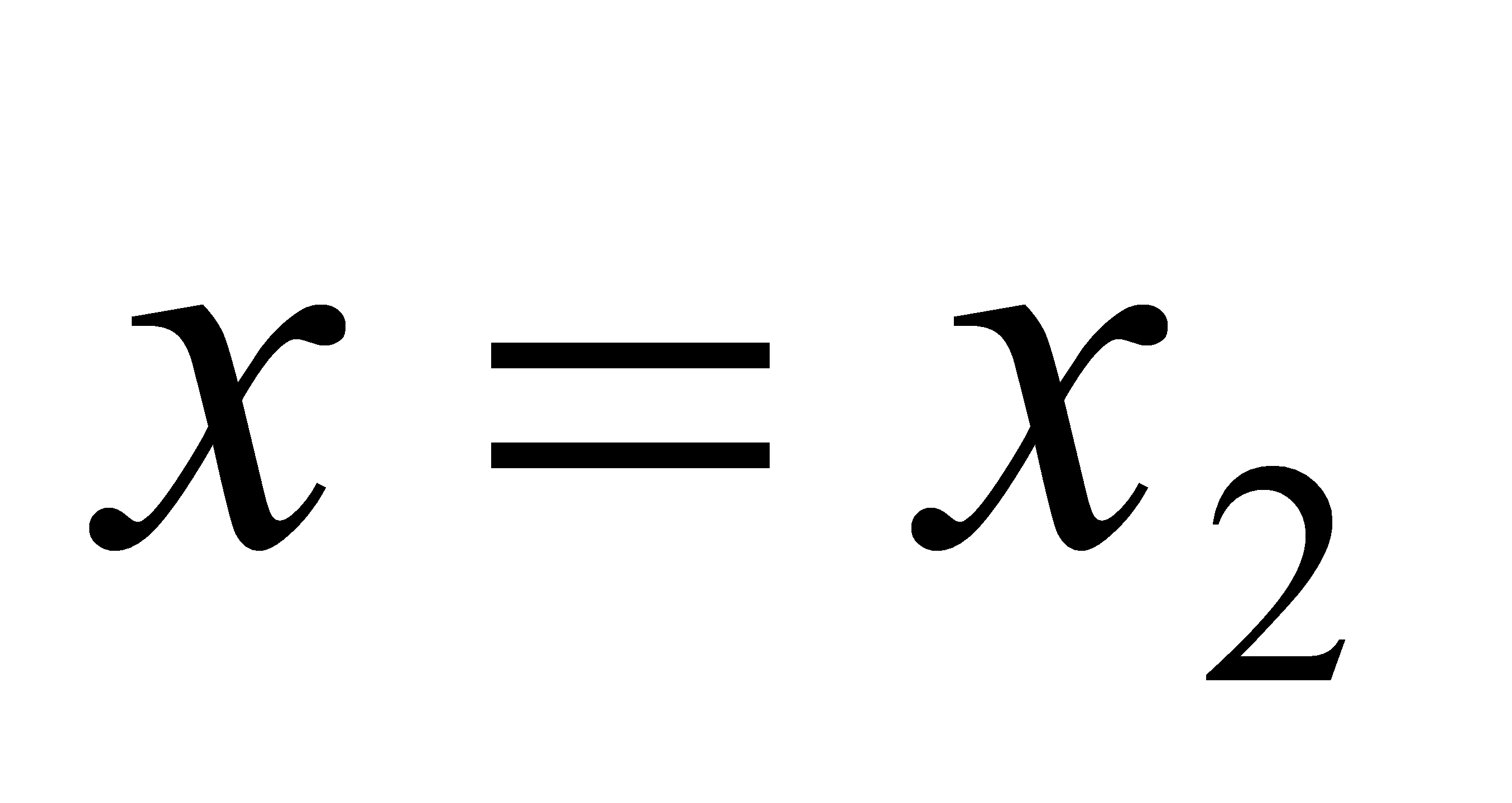і параболою, що проходить через точки 
Залишковий член формули прямокутників, трапецій, Сімпсона.
Припустимо, що у проміжку [a,b] функція f(x) має неперервні похідні перших двох порядків. Тоді, розкладаючи f(x) (по формулі Тейлора) за степенями двочлена 
аж до його квадрату, будемо мати для всіх значень в [a,b]
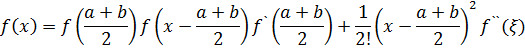
де міститься між
та
і залежить від .
Якщо про інтегрувати цю рівність у проміжку від до
, то другий член з права зникне, бо
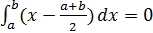. Таким чином, отримаємо 
, так, що залишковий член формули, який поновлює її точність має вигляд 
.
Позначивши через і
, відповідно найменше та найбільше значення неперервної функції f``(x) у проміжку [a,b] і користуючись тим, що другий множник підінтегрального виразу не змінює знака, за узагальненою теоремою про середнє можемо написати
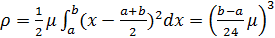
де міститься між точками
и
. По відомій властивості неперервної функції, знайдеться в [a,b] така точка
, що
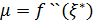, і остаточно: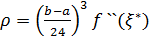 
Якщо зараз розділити проміжок [a,b] на рівних частин, то для кожного часткового проміжку
будемо мати точну формулу: 
.
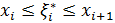Додавши ці рівності (при ) отримаємо при звичайних скорочених позначеннях
Де вираз: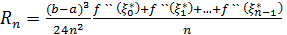 
і є залишковий член формули прямокутників. Так як вираз: 
також знаходиться між і
, то і він представляє одне із значень функції
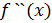. Тому остаточно маємо 
.
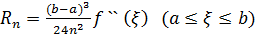Залишковий член формули трапеції.
При попередніх здогадках відносно функції f(x). Скориставшись інтерполяційною формулою Лагранжа із залишковим членом можемо написати
.
Інтегруючи цю формули від до
, знайдемо
,
так що залишковий член формули (6) буде
.
Як і вище, і користуючись тим, що другий множник підінтегральної функції і тут не змінює знака, знайдемо
.
Для випадку ділення проміжку на рівних частин
.
Таким є залишковий член формули трапецій. При зростанні він також зменшується приблизно як
. Ми бачимо, що застосування формули трапецій приводить до похибки того ж порядку, що і для формули прямокутників.
Залишковий член формули Сімпсона.
Звернемося, до формули. Можна було б, аналогічно тому, як це було зроблено вище, знов скористатись формулою Лагранжа з залишковим членом і покласти:
Про інтегрувавши рівність (15), ми не змогли б спростити інтегральний вираз для додаткового члену за допомогою теореми про середнє, бо вираз в підінтегральній функції вже змінює знак на проміжку
. Тому ми зробимо інакше.
Вираз: ,
яким би не було число , в точках
,
,
приймає одні і ті ж значення, що і функція
. Легко підібрати число
так, щоб і похідна цього виразу при
співпадала з похідною
. Таким чином, при цьому значенні
ми маємо не що інше, як інтерполяційний многочлен Ерміта, який відповідає простим вузлам
,
і двократному вузлу
. Скориставшись формулою Ерміта з залишковим членом – в припущенні існування для функції
похідних до четвертого порядку включно – отримаємо:
.
Тепер про інтегрувавши цю рівність від до
; ми знайдемо, що
так як .
Якщо припустити похідну неперервною, то, як і в попередніх випадках, залишковий член формули (8)
,
користуючись тим, що другий множник в підінтегральному виразі не змінює знак, можна підставити в такому вигляді:
.
Якщо проміжок розділити на
рівних частин, то – для формули Сімпсона– отримаємо залишковий член у вигляді
.При зростанні
цей вираз зменшується приблизно як
; таким чином, формула Сімпсона дійсно більш вигідна, ніж попередні дві формули.
РОЗДІЛ II. СЕРЕДОВИЩЕ ПРОГРАМУВАННЯ ECLIPSE
