Включите кнопку «Упругий» справа внизу. Установите, нажимая мышью на кнопки регуляторов, значение массы первой тележки m1 и ее начальную скорость 
, указанные в табл. 1 для вашей группы. Для массы второй тележки выберите минимальное значение. Ее начальную скорость выберите равной 
= - .
Нажимая мышью на кнопку «СТАРТ» на экране монитора, следите за движением тележек, останавливая движение после первого столкновения кнопкой «СТОП». Результаты измерений необходимых величин записывайте в таблицу 2, образец которой приведен ниже. Измените на 1 кг значение массы второй тележки и повторите измерения.
ЭКСПЕРИМЕНТ 2. Исследование абсолютно неупругого удара
Нажмите кнопку «Неупругий» справа внизу. Установите, нажимая мышью на кнопки регуляторов, значение масс тележек и их начальные скорости, указанные в табл. 1 для вашей группы. Проведите измерения, аналогичные эксперименту 1. Результаты запишите в таблицу 3, образец которой приведен ниже.
Таблица 1. Значения для первого и второго экспериментов(не перерисовывать).
| Номер группы | m1 (кг) | 
(м/с)
| Номер группы | m1 (кг) |
(м/с)
| |
Таблица 2. Результаты измерений и расчетов для абсолютно упругого удара (количество измерений и строк = 10)
| Номер | m1 =___, = - = ___
| ||||
| измерения | m2 (кг) | 
(м/с)
| 
(м/с)
| 
(Дж)
| 
(Дж)
|
| ... |
Таблица 3. Результаты измерений и расчетов для абсолютно неупругого удара (количество измерений и строк = 10)
| Номер измерения | m1 =___, = - = ___
| |||||||
| m2 (кг) | 
(м/с)
| 
(Дж)
|
(Дж)
| dизм | dРАСЧ | b | x | |
| -1 | ||||||||
| -1 | ||||||||
| ... | -1 |
Таблица 4. Результаты измерений и расчетов для абсолютно неупругого удара (количество измерений и строк = 11)
| Номер измерения | m2 = m1 =___, = ___
| |||||||
|
(м/с)
|
(м/с)
|
(Дж)
|
(Дж)
| dизм | dРАСЧ | b | x | |
| -0.2 | ||||||||
| ... |
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
Вычислите требуемые величины и заполните таблицы 2 – 4.
Постройте графики зависимостей относительного значения тепловой энергии d а) от отношения 
при b = -1 и
б) от отношения 
при x = 1.
Проанализируйте графики и сделайте выводы.
Вопросы и задания для самоконтроля
1. Что такое удар (столкновение, соударение)?
2. Для какого взаимодействия двух тел можно применять модель столкновения?
3. Какое столкновение называют абсолютно неупругим?
4. Какое столкновение называют абсолютно упругим?
5. При каком столкновении выполняется закон сохранения импульса?
6. Дайте словесную формулировку закона сохранения импульса.
7. При каком столкновении выполняется закон сохранения кинетической энергии?
8. Дайте словесную формулировку закона сохранения кинетической энергии.
9. Дайте определение кинетической энергии.
10. Дайте определение потенциальной энергии.
11. Что такое полная механическая энергия.
12. Что такое замкнутая система тел?
13. Что такое изолированная система тел?
14. При каком столкновении выделяется тепловая энергия?
15. При каком столкновении форма тел восстанавливается?
16. При каком столкновении форма тел не восстанавливается?
ЛАБОРАТОРНАЯ РАБОТА № 3
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Ознакомьтесь с конспектом лекций и учебником (Савельев, т.1, § 49, 50, 53, 58). Запустите программу «Открытая физика». Выберите «Механические колебания и волны» и «Свободные колебания» (сначала математический маятник, потом груз на пружине). Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ еще раз)
ЦЕЛЬ РАБОТЫ:
* Выбор физических моделей для анализа движения тел.
* Исследование движения тела под действием квазиупругой силы.
* Экспериментальное определение зависимости частоты колебаний от параметров системы.
КРАТКАЯ ТЕОРИЯ:
КОЛЕБАНИЕ - периодически повторяющееся движения тела. ПЕРИОД T – минимальное время, через которое движение полностью повторяется.
ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ – движение, при котором координата тела меняется со временем по закону синуса или косинуса: 
.
Основными характеристиками гармонических колебаний являются:
АМПЛИТУДА А 0 – максимальное значение параметра А.
ЦИКЛИЧЕСКАЯ ЧАСТОТА собственных колебаний w0 – в 2p раз большая обычной или линейной частоты n = 1/ Т (n - число полных колебаний за единицу времени).
ФАЗА (w0 t + j0) – значение аргумента косинуса.
НАЧАЛЬНАЯ ФАЗА j0 – значение аргумента косинуса при t = 0.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных гармонических колебаний параметра А: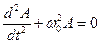 
, свободных затухающих колебаний:
, где b – коэффициент затухания.
МАТЕМАТИЧЕСКИЙ МАЯТНИК (ММ) и ПРУЖИННЫЙ МАЯТНИК (ПМ) это МОДЕЛИ объектов, в которых могут происходить гармонические колебания.
ММ это материальная точка, подвешенная на идеальной (невесомой и нерастяжимой) нити.
ПМ это материальная точка, прикрепленная к идеальной (невесомой и подчиняющейся закону Гука) пружине. Формулы для w0 в этих системах выпишите из конспекта или учебника.
ЗАДАНИЕ: Выведите формулу для циклической частоты свободных колебаний кубика на пружине, лежащего на горизонтальной абсолютно гладкой поверхности.
УКАЗАНИЯ: Выпишите формулу для второго закона Ньютона. Подставьте в нее все реальные силы, действующие на кубик. Спроектируйте полученное векторное уравнение на вертикальную и горизонтальную оси. Проведя тождественные преобразования, получите уравнение, похожее на дифференциальное уравнение свободных колебаний. Константу, являющуюся множителем перед А, приравняйте к квадрату циклической частоты, откуда получите w.
МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ
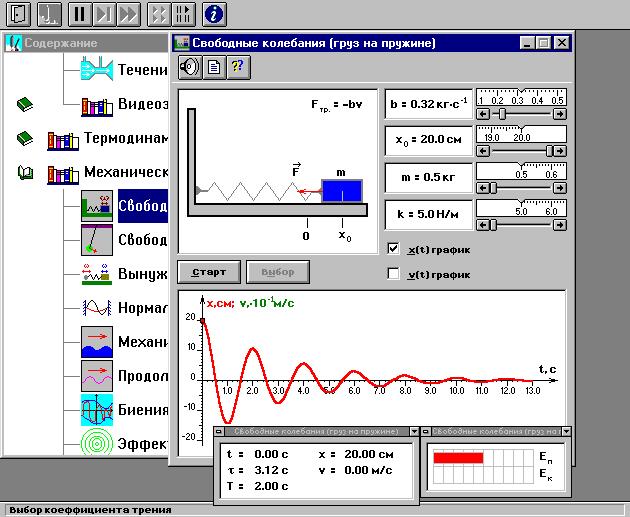
Внимательно рассмотрите рисунки, найдите все регуляторы и другие основные элементы. Зарисуйте поле движения тела с регуляторами соответствующих параметров (укажите, что они регулируют).
ЭКСПЕРИМЕНТ 1.
Выберите «Маятник». Установите с помощью движков регуляторов максимальную длину нити L и значения коэффициента затухания и начального угла, указанные в табл. 1 для вашей группы.
Нажимая мышью на кнопку «СТАРТ», следите за движением точки на графиках угла и скорости и за поведением маятника. Потренируйтесь, останавливая движение кнопкой «СТОП» (например, в максимуме смещения), и запуская далее кнопкой «СТАРТ». Выберите число полных колебаний N = 3 – 5 и измеряйте их продолжительность D t (как разность t 2– t 1 из таблицы на экране).
Приступайте к измерениям длительности D t для N (3-5) полных колебаний, начиная с максимальной длины (150 см) нити маятника и уменьшая ее каждый раз на 10 см (до минимальной длины 80 см). Длину нити L и результаты измерений длительности D t записывайте в таблицу 2, образец которой приведен ниже.
ЭКСПЕРИМЕНТ 2
Выберите «Груз на пружине». Установите массу груза, значение коэффициента затухания и начальное смещение, указанные в табл. 1 для вашей группы. Проведите измерения, аналогичные эксперименту 1, уменьшая коэффициент жесткости k каждый раз на 1 Н/м.
Таблица 1. Значения коэффициента затухания (вязкого трения), начального угла отклонения (для первого эксперимента) и начального отклонения (для второго).
| Номер группы | b (кг/с) | j0 (0) | X 0 (см) | m (кг) |
| 0.8 | 0.5 | |||
| 0.6 | 0.6 | |||
| 0.4 | 0.7 | |||
| 0.2 | 0.8 | |||
| 0.08 | 0.7 | |||
| 0.07 | 0.8 | |||
| 0.06 | 0.9 | |||
| 0.05 | 1.0 |
Таблица 2. Результаты измерений (количество измерений и строк = 8)
| Номер измерения | N = | |||
| L (м) | D t (с) | Т (с) | Т 2(с2) | |
| 1.5 | ||||
| 1.4 | ||||
| ... | ||||
| g (м/с2) |
Таблица 3. Результаты измерений (количество измерений и строк = 6)
| Номер измерения | N = | ||||
| k (H/м) | D t (с) | Т (с) | w(1/с) | w2(1/с2) | |
| ... |
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
Вычислите требуемые величины и заполните таблицы 2 и 3.
Постройте графики зависимости
· квадрата периода колебаний от длины нити ММ,
· квадрата циклической частоты колебаний от жесткости пружины ПМ.
По наклону графика Т 2 = f (L) определите значение g, используя формулу
. Оцените абсолютную ошибку определения g.
По наклону графика w2 = f (k) определите значение m используя формулу
. Оцените абсолютную ошибку определения m.
Проанализируйте ответ и графики.
Вопросы и задания для самоконтроля
1. Что такое колебание?
2. Дайте определение периода колебаний.
3. Дайте определение частоты колебаний.
4. Дайте определение гармонических колебаний.
5. Запишите закон зависимости от времени характеристики А, совершающей гармоническое колебательное изменение.
6. Запишите закон движения МТ, совершающей гармонические колебания.
7. Дайте определение амплитуды гармонических колебаний.
8. Дайте определение фазы гармонических колебаний.
9. Дайте определение начальной фазы гармонических колебаний.
10. Напишите уравнение связи частоты и периода гармонических колебаний.
11. Напишите уравнение связи частоты и циклической частоты гармонических колебаний.
12. Напишите формулу зависимости скорости МТ от времени при гармонических колебаниях.
13. Напишите уравнения связи амплитуды скорости и амплитуды смещения при гармонических колебаниях МТ.
14. Напишите формулу зависимости ускорения МТ от времени при гармонических колебаниях.
15. Напишите уравнения связи амплитуды скорости и амплитуды ускорения при гармонических колебаниях МТ.
16. Напишите уравнения связи амплитуды смещения и амплитуды ускорения при гармонических колебаниях МТ.
17. Напишите дифференциальное уравнение свободных гармонических колебаний МТ.
18. Напишите дифференциальное уравнение свободных затухающих колебаний МТ.
19. Что определяет коэффициент затухания?
20. Дайте определение математического маятника.
21. Запишите формулу циклической частоты свободных колебаний математического маятника.
22. Дайте определение пружинного маятника.
23. Запишите формулу циклической частоты свободных колебаний пружинного маятника.
24. Какие процессы происходят при вынужденных колебаниях?
25. Что такое резонанс?
26. При каком затухании резонанс будет более резким?
