19. Тело массой m = 2,0 кг движется прямолинейно по закону s = A – Bt + + Ct 2 – Dt 3, где A = 6,0 м, B = 3,0 м/с, C = 2,0 м/c2, D = 0,40 м/с3. Определить силу, действующую на тело в конце первой секунды движения.
Ответ: F =  (t) m = 3,2 Н.
(t) m = 3,2 Н.
20. Простейшая машина Атвуда, применяемая для изучения законов равноускоренного движения, представляет собой два груза с различными массами m 1 и m 2 (например, m 1> m 2), которые подвешены на нити, перекинутой через легкий неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, найти: а) ускорение грузов a; б) силу натяжения нити T; в) силу, действующую на ось блока F.
Ответ: а) 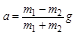 ;
;
б) 
в) 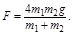
21. Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол a с горизонтом. Найти коэффициент трения, если время подъема тела в h раз меньше времени спуска.
Ответ: m = [(h2 – 1)/(h2 + 1)]tga.
22. В момент t = 0 частица массой m начинает двигаться под действием силы  , где
, где  и w – постоянные. Сколько времени частица будет двигаться до первой остановки? Какой путь она пройдет за это время? Какова максимальная скорость частицы на этом пути?
и w – постоянные. Сколько времени частица будет двигаться до первой остановки? Какой путь она пройдет за это время? Какова максимальная скорость частицы на этом пути?
Ответ: t = p/w; s = 2 F 0 /m w2; u макс = F 0 /m w.
23. На горизонтальной плоскости с коэффициентом трения m лежит тело массой m. В момент t = 0 к нему приложили горизонтальную силу, зависящую от времени как  , где
, где  – постоянный вектор. Найти путь, пройденный телом за первые t секунд действия этой силы.
– постоянный вектор. Найти путь, пройденный телом за первые t секунд действия этой силы.
Ответ:  , где
, где  – момент времени, с которого начнется движение. При
– момент времени, с которого начнется движение. При  путь s = 0.
путь s = 0.
24. На гладкой горизонтальной плоскости лежит доска массой m 1 и на ней брусок массой m 2. К бруску приложили горизонтальную силу, увеличивающуюся со временем t по закону F = a t, где a – постоянная. Найти зависимость от t ускорений доски а 1 и бруска а 2, если коэффициент трения между доской и бруском равен m. Изобразить примерные графики этих зависимостей.
Ответ: При t £ t 0 ускорения а 1 = а 2 = a t/ (m 1 + m 2); при t ³ t 0 a 1 = m gm 2/ m 1,
a 2 = (a t – m m 2 g)/ m 2. Здесь t 0 = m gm 2(m 1 + m 2)/a m 1.
25. На наклонную плоскость с углом наклона к горизонту α = 35  положена доска массой m 2 = 2,0 кг, а на нее – брусок массой m 1 = 1,0 кг. Коэффициент трения между бруском и доской m1 = 0,10, а между доской и плоскостью – m2 = 0,20. Определить: а) ускорение бруска a 1; б) ускорение доски a 2; в) коэффициент трения m2, при котором доска не будет двигаться.
положена доска массой m 2 = 2,0 кг, а на нее – брусок массой m 1 = 1,0 кг. Коэффициент трения между бруском и доской m1 = 0,10, а между доской и плоскостью – m2 = 0,20. Определить: а) ускорение бруска a 1; б) ускорение доски a 2; в) коэффициент трения m2, при котором доска не будет двигаться.
Ответ: а) 
б) 

в) 
26. Тело массой m бросили под углом к горизонту с начальной скоростью 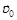 . Пренебрегая сопротивлением воздуха, найти:
. Пренебрегая сопротивлением воздуха, найти:
а) приращение импульса тела за первые t секунд движения;
б) модуль приращения импульса тела за все время движения.
Ответ: а)  ; б)
; б)  .
.
27. Снаряд, вылетевший из орудия со скоростью u 0, разрывается в верхней точке траектории на два осколка, разлетающиеся горизонтально. Один из них полетел в обратном направлении со скоростью, равной скорости снаряда до разрыва. Пренебрегая сопротивлением воздуха, определить, на каком расстоянии s по горизонтали от орудия упадет второй осколок, если верхняя точка траектории отстояла от орудия на расстояние l по горизонтали.
Ответ: s = 4 l.
28. Платформа массой m 0 начинает двигаться вправо под действием постоянной силы  (см. рис.). Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна m кг/с. Найти зависимости от времени скорости и ускорения платформы в процессе погрузки. Трение пренебрежимо мало.
(см. рис.). Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна m кг/с. Найти зависимости от времени скорости и ускорения платформы в процессе погрузки. Трение пренебрежимо мало.
Ответ:
 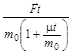 , ,
 . .
|

|
29. Тележка с песком движется по горизонтальной плоскости под действием постоянной силы  , совпадающей по направлению с ее скоростью. При этом песок высыпается через отверстие в дне с постоянной скоростью m кг/с. Найти ускорение и скорость тележки в момент времени t, если в момент t = 0 тележка с песком имела массу m 0и ее скорость была равна нулю. Трением пренебречь.
, совпадающей по направлению с ее скоростью. При этом песок высыпается через отверстие в дне с постоянной скоростью m кг/с. Найти ускорение и скорость тележки в момент времени t, если в момент t = 0 тележка с песком имела массу m 0и ее скорость была равна нулю. Трением пренебречь.
Ответ:  ;
; 
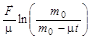 .
.
30. Ракета поднимается с нулевой начальной скоростью вертикально вверх. Начальная масса ракеты m 0, скорость истечения газа относительно ракеты постоянна и равна u. Пренебрегая сопротивлением воздуха, выразить скорость ракеты u в зависимости от m и t (m – масса ракеты и t – время полета). Поле сил тяжести считать однородным.
Ответ: 
31. Тело массой m бросили под углом a к горизонту с начальной скоростью u 0. Найти среднюю мощность, развиваемую силой тяжести за все время движения тела, и мгновенную мощность этой силы как функцию времени.
Ответ: < P > = 0, P (t) = mg (gt – u 0 sin a).
32. Небольшое тело массой m начинает скользить без трения с вершины наклонной плоскости, высота которой h и угол наклона к горизонту a (см.

| рис.). Найти модуль момента импульса тела  относительно оси О, перпендикулярной к плоскости рисунка, через время t после начала движения.
Ответ: относительно оси О, перпендикулярной к плоскости рисунка, через время t после начала движения.
Ответ:  = (1/2) mght× sin2a. = (1/2) mght× sin2a.
|
33. Уравнение движения материальной точки массой 5 г имеет вид х = 4sin(2p t /8+2) (см). Определить амплитуду колебаний, циклическую частоту, период колебаний, начальную фазу, максимальную скорость, максимальное ускорение, максимальную силу, поддерживающую это движение и полную энергию колеблющейся точки.
Ответ: х макс. = 4 см; w = p/4 с-1; Т = 2p/w = 8 с; u макс = х макс.w = 3,1 см/с;
а макс = 2,5 см/с2; F макс = 1,3×10–4 Н; Е = 2,5×10–6 Дж.
34. Тело массой m движется в плоскости xy по закону 
 , где A, B, ω – некоторые постоянные. Определить модуль силы F, действующей на это тело.
, где A, B, ω – некоторые постоянные. Определить модуль силы F, действующей на это тело.
Ответ: 
35. За время t = 16,1 с амплитуда колебаний уменьшается в a = 5,00 раз. Найти: a) коэффициент затухания b; б) за какое время t амплитуда уменьшится в е раз?
Ответ: а) b = 0,100 с-1; б) t = 10,0 с.
36. Для плоской монохроматической волны смещение от положения равновесия точки, находящейся на расстоянии 4,0 см от источника колебаний, через промежуток времени Т /6 равно половине амплитуды. Определить длину волны.
Ответ: l = 0,48 м.
ЗАКОНЫ СОХРАНЕНИЯ
37. Две одинаковые тележки движутся друг за другом по инерции (без трения) с одной и той же скоростью 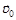 . На задней тележке находится человек массой m. В некоторый момент человек прыгнул в переднюю тележку со скоростью
. На задней тележке находится человек массой m. В некоторый момент человек прыгнул в переднюю тележку со скоростью  относительно своей тележки. Масса каждой тележки равна M. Найти скорости, с которыми будут двигаться обе тележки после прыжка.
относительно своей тележки. Масса каждой тележки равна M. Найти скорости, с которыми будут двигаться обе тележки после прыжка.
Ответ:  ,
, 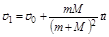 .
.
38. Платформа с песком общей массой M = 2,0 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой m = 8,0 кг и застревает в нем. Пренебрегая трением, определить с какой скоростью будет двигаться платформа, если в момент попадания скорость снаряда u = 450 м/с, а его направление – сверху вниз под углом α = 30° под углом к горизонту.
Ответ: u = mu cosa / (M + m) = 1,6 м/с.
39. Пушка массой М начинает свободно скользить вниз по гладкой наклонной плоскости, составляющей угол a с горизонтом. Когда пушка прошла путь l, произвели выстрел, в результате которого снаряд вылетел с импульсом  в горизонтальном направлении, а пушка остановилась. Пренебрегая массой снаряда по сравнению с массой пушки, найти продолжительность выстрела.
в горизонтальном направлении, а пушка остановилась. Пренебрегая массой снаряда по сравнению с массой пушки, найти продолжительность выстрела.
Ответ:  .
.
40. На катере массой m = 4,5 т находится водомет, выбрасывающий со скоростью u = 6,0 м/с относительно катера воду с расходом μ = 25 кг/с. Пренебрегая сопротивлением движению катера, определить: а) скорость катера u через t = 3,0 мин после начала движения; б) предельно возможную скорость катера u max.
Ответ: u (t) =  следовательно:
следовательно:
а) u = 3,8 м/с; б) u max = u = 6,0 м/с.
41. Ствол пушки направлен под углом q = 45° к горизонту. Когда колеса пушки закреплены, скорость снаряда, масса которого в h = 50 раз меньше массы пушки, u 0 = 180 м/с. Найти скорость пушки сразу после выстрела, если колеса ее освободить.
Ответ: u = u 0 cosq /(1 + h) = 25 м/c.
42. Шайба массой m соскальзывает без начальной скорости по наклонной плоскости, составляющей угол a с горизонтом, и, пройдя по горизонтальной плоскости расстояние l, останавливается. Найти работу сил трения на всем пути, считая всюду коэффициент трения равным m.
Ответ: А тр = m mgl / (1 – m ctga).
43. Тело массой m начинает двигаться под действием силы 
 , где
, где  и
и  – орты осей x и y соответственно. Определить мощность N (t), развиваемую силой в момент времени t.
– орты осей x и y соответственно. Определить мощность N (t), развиваемую силой в момент времени t.
Ответ: 
44. Поезд массой m = 600 т движется под гору с уклоном α = 0,3° и за время t = 1 мин развивает скорость u = 18 км/ч. Коэффициент трения m = 0,01. Определить среднюю мощность локомотива  .
.
Ответ: 
45. Потенциальная энергия частицы в некотором силовом поле определяется выражением U = 1,0 x + 2,0 y 2 + 3,0 z 3 (U в Дж, координаты в м). Найти работу А, совершаемую над частицей силами поля при переходе из точки с координатами (1,0; 1,0; 1,0) в точку с координатами (2,0; 2,0; 2,0).
Ответ: А = –28 Дж.
46. К нижнему концу пружины жесткостью k 1 прикреплена другая пружина жесткостью k 2, к концу которой прикреплена гиря. Пренебрегая массой пружин, определить отношение их потенциальных энергий.
Ответ: 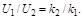
47. Потенциальная энергия частицы в некотором поле имеет вид  , где aи b – положительные постоянные, r – расстояние от центра поля. Найти: а) значение r 0, соответствующее равновесному положению частицы; выяснить, устойчиво ли это положение; б) максимальное значение силы притяжения; в) изобразить примерные графики зависимостей
, где aи b – положительные постоянные, r – расстояние от центра поля. Найти: а) значение r 0, соответствующее равновесному положению частицы; выяснить, устойчиво ли это положение; б) максимальное значение силы притяжения; в) изобразить примерные графики зависимостей 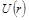 и Fr (r) – проекции силы на радиус-вектор
и Fr (r) – проекции силы на радиус-вектор  .
.
Ответ: а)  , б)
, б)  .
.
48. Материальная точка массой m брошена под углом a к горизонту с начальной скоростью 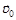 . Траектория полета частицы лежит в плоскости ХY, ось Z направлена «на нас». Пренебрегая сопротивлением воздуха, найти зависимость от времени: а) момента силы, действующей на частицу; б) момента импульса частицы. Оба момента берутся относительно точки бросания.
. Траектория полета частицы лежит в плоскости ХY, ось Z направлена «на нас». Пренебрегая сопротивлением воздуха, найти зависимость от времени: а) момента силы, действующей на частицу; б) момента импульса частицы. Оба момента берутся относительно точки бросания.
Ответ: а) 

 , б)
, б) 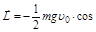

 .
.
49. Шарик массой m бросили под углом a к горизонту с начальной скоростью u 0. а) Найти модуль момента импульса L шарика относительно точки бросания в зависимости от времени движения; б) вычислить L в вершине траектории, если m = 130 г, a = 45° и u 0 = 25 м/с. Сопротивлением воздуха пренебречь.
Ответ: а) L = (1/2) mgu 0 t 2 × cosa;
б) L = (mu 03/2 g)sin2acosa = 37 кг×м2/с.
50. Небольшой шарик массой m, привязанный на нити длиной l к потолку в точке О, движется по горизонтальной окружности так, что нить вращается вокруг вертикальной оси с постоянной угловой скоростью w. Относительно каких точек момент импульса  шарика остается постоянным? Найти модуль приращения момента импульса шарика относительно точки О за половину оборота.
шарика остается постоянным? Найти модуль приращения момента импульса шарика относительно точки О за половину оборота.
Ответ: относительно центра окружности;  .
.
51. Однородный шар скатывается без скольжения по наклонной плоскости, составляющей угол a с горизонтом. Найти ускорение центра шара и значение коэффициента трения, при котором скольжения не будет.
Ответ:  ,
,  .
.
52. На однородный сплошной цилиндр массой М и радиусом R плотно намотана легкая нить, к концу которой прикреплен груз массой m (см. рис.). В момент t = 0система пришла в движение. Пренебрегая трением
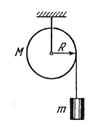
| в оси цилиндра, найти зависимость от времени: а) модуля угловой скорости цилиндра; б) кинети-ческой энергии всей системы.
Ответ: а)  ,
б) ,
б)  . .
|
Тестовые вопросы и качественные
Задачи по механике
1. При каком характере движения частицы имеет место равенство ç<  >ô = <
>ô = < 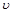 >?
>?
2. Тело брошено под углом к горизонту со скоростью 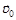 . Показать на рисунке среднюю скорость <
. Показать на рисунке среднюю скорость <  > и среднее ускорение <
> и среднее ускорение <  > за все время движения. Сопротивление не учитывать.
> за все время движения. Сопротивление не учитывать.
3. Частица ударяется о стенку и упруго отражается от нее так, что угол падения a равен углу отражения. Найти êD  ï,ïD
ï,ïD  ï х, ïD
ï х, ïD  ï y, где
ï y, где  – скорость частицы.
– скорость частицы.
4. Зависимость радиус-вектора частицы от времени дается законом  , где a и b – положительные постоянные. Найти: а) уравнение траектории в параметрической форме x = x (t), y = y (t); б) уравнение траектории в виде y (x); в) скорость
, где a и b – положительные постоянные. Найти: а) уравнение траектории в параметрической форме x = x (t), y = y (t); б) уравнение траектории в виде y (x); в) скорость  и ускорение
и ускорение  частицы; г) мо-дули скорости u и ускорения а; д) среднюю скорость частицы á
частицы; г) мо-дули скорости u и ускорения а; д) среднюю скорость частицы á  ñ за время от 0 до t; е) в произвольной точке траектории изобразить векторы
ñ за время от 0 до t; е) в произвольной точке траектории изобразить векторы 
5. Частица движется по криволинейной траектории. Имеют ли какой-либо физический смысл (и какой, если имеют) следующие выражения:
a)  б)
б)  в)
в)  г)
г) 
д) 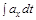 e)
e)  ж)
ж)  з)
з)  ?
?
6. Модуль скорости u частицы меняется со временем t по закону u = g+ b t, где g и b – положительные постоянные. Модуль ускорения а = 3g. Найти тангенциальное и нормальное ускорения, а также радиус кривизны R траектории в зависимости от t.
7. Нормальное ускорение частицы постоянно по модулю. Что можно сказать о форме траектории частицы в случаях, когда проекция тангенциального ускорения на направление движения а) равна нулю; б) положительная; в) отрицательная.
8. Диск вращается вокруг неподвижной оси, проходящей через его центр и перпендикулярной его плоскости. В некоторый момент времени известны угловая скорость вращения ( ) и угловое ускорение (
) и угловое ускорение ( ) диска. Найти скорость
) диска. Найти скорость  и ускорение произвольной точки А диска, положение которой задается вектором
и ускорение произвольной точки А диска, положение которой задается вектором  , проведенным из центра диска. Рассмотреть случаи: а)
, проведенным из центра диска. Рассмотреть случаи: а)  и
и  параллельны; б)
параллельны; б)  и
и  антипараллельны. Ответы проиллюстрировать рисунками.
антипараллельны. Ответы проиллюстрировать рисунками.
9. Тело вращается вокруг неподвижной оси так, что угол его поворота меняется в зависимости от времени t по закону j = 2p(a t – b t 3), где a и b – положительные постоянные. Найти среднюю угловую скорость áwñ и среднее угловое ускорение ábñ за все время движения.
10. Шайбу массой m пустили вверх по горке с начальной скоростью 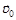 . Добравшись до некоторой высоты, она соскальзывает вниз, имея у основания скорость
. Добравшись до некоторой высоты, она соскальзывает вниз, имея у основания скорость  . Найти работу сил трения за все время движения.
. Найти работу сил трения за все время движения.
11. Частица массой m движется в положительном направлении оси Х. Найти ее момент импульса относительно точки О (начало координат) и точки О¢, имеющей координаты (0; а; 0).
12. Система состоит из двух тел. Известны зависимости от времени импульсов этих тел:  и
и  .
.
а) Сохраняется ли импульс системы?
б) Сохраняются ли какие либо проекции импульса на декартовые оси координат?
в) Чему равна результирующая всех сил, приложенных к телам?
13. Частица m движется в плоскости ху по окружности радиуса R. Скорость частицы  и тангенциальное ускорение
и тангенциальное ускорение  . Найти момент импульса частицы
. Найти момент импульса частицы 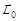 и момент сил
и момент сил  относительно центра окружности О.
относительно центра окружности О.
14. Диск катится по горизонтальной поверхности без проскальзывания со скоростью  . Масса диска m, радиус R. Найти его момент импульса и кинетическую энергию относительно точки О, лежащей в плоскости движения на этой горизонтальной поверхности.
. Масса диска m, радиус R. Найти его момент импульса и кинетическую энергию относительно точки О, лежащей в плоскости движения на этой горизонтальной поверхности.
15. Тангенциальное ускорение при движении по криволинейной траектории изменяется по закону а t = a s, где a – положительная постоянная. Масса частицы m. Чему равна работа сил А на пути s?
16. Изобразить эквипотенциальные поверхности, а также силу  и градиент потенциала
и градиент потенциала  U в некоторой точке поля, создаваемого зарядом q.
U в некоторой точке поля, создаваемого зарядом q.
17. Частица, положение которой относительно начала отсчета дается радиус-вектором  (–3, 2, –7) (м), имеет импульс
(–3, 2, –7) (м), имеет импульс 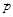 (2, 4, 3) (кг×м/с). Определить: а) момент импульса
(2, 4, 3) (кг×м/с). Определить: а) момент импульса  относительно начала отсчета, б) моменты импульсов относительно осей X, Y, Z.
относительно начала отсчета, б) моменты импульсов относительно осей X, Y, Z.
18. U (x, y, z) = a x 2 + b y 2 – g z 2. Определить: а) силу  , действующую на частицу; б) работу А, совершаемую силой поля при перемещении частицы из точки 1 (x 1, y 1, z 1) в точку 2 (x 2, y 2, z 2).
, действующую на частицу; б) работу А, совершаемую силой поля при перемещении частицы из точки 1 (x 1, y 1, z 1) в точку 2 (x 2, y 2, z 2).
19. Частица m движется в плоскости ху по окружности радиуса R с an = ct 2. Найти: момент импульса  и момент силы
и момент силы  относительно центра окружности О.
относительно центра окружности О.
20. Сплошной цилиндр массой m и радиуса R вращается с угловой скоростью  вокруг оси z, совпадающей с одной из образующих цилиндрической поверхности. Найти импульс
вокруг оси z, совпадающей с одной из образующих цилиндрической поверхности. Найти импульс 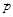 цилиндра, момент импульса
цилиндра, момент импульса  и кинетическую энергию цилиндра Е к.
и кинетическую энергию цилиндра Е к.
21. Чему равно отношение кинетических энергий вращательного и поступательного движения тонкого проволочного кольца, скатывающегося без проскальзывания с наклонной плоскости?
22. Частица движется по замкнутой траектории в центральном силовом поле, где ее потенциальная энергия U = kr 2, где k – положительная постоянная, r – расстояние частицы до центра поля О. Найти массу частицы, если наименьшее расстояние ее до точки О равно r 1, а скорость на наибольшем расстоянии  .
.






