ВРАЩАТЕЛЬНО движения
1. Инерциальной системой отсчета называется система
1. в которой выполняется первый закон Ньютона
2. в которой действуют только консервативные силы
3. которая движется равномерно и прямолинейно
4. которая движется с ускорением
5. центр которой совмещен с Солнцем, а координатные оси направлены на соответствующим образом выбранные звезды
2. Автомобиль движется равномерно и прямолинейно со скоростью 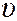 . Равнодействующая всех сил, действующих на автомобиль
. Равнодействующая всех сил, действующих на автомобиль
1. не изменяется со временем и действует по направлению движения
2. не изменяется со временем и действует против направления движения
3. не изменяется со временем по величине и направлению
4. равна нулю
5. изменяется со временем по величине
3. Законы Ньютона применимы для описания движения тел
1. в инерциальных и неинерциальных системах отсчета
2. только в инерциальных системах отсчета
3. только при движении со скоростями, много меньшими скорости света в любых системах отсчета
4. в инерциальных системах отсчета при движении тел с любыми скоростями
5. в инерциальных системах отсчета при движении со скоростями, много меньшими скорости света
 4. На тело, движущееся со скоростью
4. На тело, движущееся со скоростью 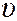 , действует сила
, действует сила  . Вектор ускорения тела имеет направление
. Вектор ускорения тела имеет направление
 5. Равнодействующая всех сил, действующих на материальную точку, имеет направление
5. Равнодействующая всех сил, действующих на материальную точку, имеет направление
1. а 2. б 3. в
4. г 5. д
 6. Тело массой m движется под действием постоянной по модулю и направлению силы
6. Тело массой m движется под действием постоянной по модулю и направлению силы  . График, отражающий движение этого тела имеет вид
. График, отражающий движение этого тела имеет вид
а б в
г д
1. а 2. б 3. в 4. г 5. д
7. Автомобиль движется вдоль оси х согласно уравнению  . Модуль силы, действующей на автомобиль, со временем
. Модуль силы, действующей на автомобиль, со временем
1. возрастает
2. убывает
3. не изменяется
4. равен нулю
5. среди ответов 1- 4 нет правильного
8. Тело движется вдоль оси х согласно уравнению  . Модуль силы, действующей на тело, со временем
. Модуль силы, действующей на тело, со временем
1. возрастает
2. убывает
3. не изменяется
4. сначала возрастает, затем убывает
5. равен нулю
9. Тело массой 2 кг движется вдоль оси х согласно уравнению  . Сила, действующая на него в момент времени t = 2 с, равна (Н)
. Сила, действующая на него в момент времени t = 2 с, равна (Н)
1. 48 2. 63 3. 96 4. 120 5. 126
10. На материальную точку массы 1 кг действуют две постоянные взаимноперпендикулярные силы, равные 6 Н и 8 Н. Материальная точка движется с ускорением (м/с2)
1. 2 2. 6 3. 8 4. 10 5. 14
 11. Самолет во время выполнения «мертвой петли» движется равномерно по окружности. Вектор равнодействующей всех сил, действующих на самолет, имеет направление
11. Самолет во время выполнения «мертвой петли» движется равномерно по окружности. Вектор равнодействующей всех сил, действующих на самолет, имеет направление
1. 1 2. 2 3. 3 4. 4 5. 5
12. Для увеличения веса груза в 3 раза его необходимо поднимать с ускорением, равным
1. 1/3 g 2. g 3. 2 g 4. 3 g 5. 9 g
13. Деревянный брусок с постоянной скоростью соскальзывает с наклонной плоскости. Угол наклона плоскости составляет 15°. Коэффициент трения между бруском и плоскостью равен
1. arc sin 15° 2. arc cos 15° 3. arc tg 15° 4. tg 15° 5. cos 15°
14. Стержень длиной l движется по гладкой горизонтальной поверхности. В сечении стержня на расстоянии 1/4 l от конца, к которому приложена сила F, направленная вдоль стержня возникает сила, равная
1. 0 2. 1/4 F 3. 1/2 F 4. 3/4 F 5. F
15. Груз поднимают с помощью ленточного транспортера, расположенного под углом α к горизонту. Если коэффициент трения между грузом и лентой транспортера равен μ, то максимальное ускорение, с которым может подниматься груз, равно
1. μ g cos α 2. g (sin α + μ cos α)
3. g (cos α – μ sin α) 4. μ g sin α 5. μ g tg α
16. Тело массой m = 1 кг движется по плоскости таким образом, что зависимость проекций скорости тела от времени имеет вид: 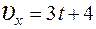 и
и 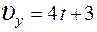 . При этом модуль равнодействующей приложенных к телу сил равен (Н)
. При этом модуль равнодействующей приложенных к телу сил равен (Н)
1. 1 2. 3 3. 4 4. 5 5. 7
17. Конькобежец массой 85 кг, стоя на коньках, бросает камень массой 5 кг со скоростью 8 м/с под углом 30° к горизонту. Конькобежец после броска приобретает скорость, равную (м/с)
1. 0,1 2. 0,2 3. 0,3 4. 0,4 5. 0,5
18. Два тела, летящие навстречу друг другу со скоростью 5 м/с каждое, после абсолютно неупругого удара стали двигаться как единое целое со скоростью 2,5 м/с. Отношение масс этих тел равно
1. 1 2. 2 3. 3 4. 1,5 5. 2,5
19. Два тела движутся по взаимно перпендикулярным направлениям. Первое тело массой 5 кг движется со скоростью 2 м/с, второе тело массой 10 кг движется со скоростью 1 м/с. После абсолютно неупругого соударения импульс шаров равен (кг · м/с)
1. 14 2. 15 3. 16 4. 18 5. 20
20. Тело массой 1 кг движется согласно уравнению  . Его кинетическая энергия равна (Дж)
. Его кинетическая энергия равна (Дж)
1. 9 2. 18 3. 36 4. 81 5. 162
21. При выстреле из винтовки вертикально вверх со скоростью 300 м/с пуля массой 10 г достигла высоты 4000 м. Величина работы, совершенной силой трения о воздух, равна (Дж)
1. 50 2. 500 3. 4500 4. 45000 5. 90000
22. Через 2 с после броска кинетическая энергия тела массы 0,2 кг, брошенного вертикально вверх со скоростью 30 м/с, равна (Дж)
1. 60 2. 30 3. 20 4. 15 5. 10
23. Тело прошло путь 10 м под действием силы, которая равномерно уменьшается от 10 Н в начале пути до 2 Н в конце. Работа силы на протяжении всего пути равна (Дж)
1. 50 2. 60 3. 80 4. 120 5. 160
24. К бруску массой 2 кг, лежащему на шероховатой горизонтальной поверхности, прикреплена легкая пружинка, коэффициент упругости которой k = 32 Н/м. Коэффициент трения между бруском и поверхностью μ = 0,8. Работа, которую нужно совершить, чтобы сдвинуть брусок с места, растягивая в горизонтальном направлении пружинку, равна (Дж)
1. 3,2 2. 4,0 3. 6,4 4. 7,6 5. 8,0
25. Тело, массой 1 кг соскользнуло по наклонной поверхности длиной 5 м, затем двигалось по горизонтальной поверхности 3 м, было поднято на высоту 3 м и горизонтально возвращено в исходную точку. Полная работа силы тяжести над телом на всем пути движения равна (Дж)
1. 0 2. 30 3. 60 4. 80 5. 210
26. Тело массой 1 кг падает с высоты 20 м. Его мгновенная мощность на высоте 10 м равна (Вт)
1. 70 2. 100 3. 140 4. 200 5. 280
27. Молот массой 5 кг ударяет небольшой кусок железа, лежащий на наковальне. Масса наковальни равна 100 кг. Массой куска железа пренебречь. Удар неупругий. КПД удара молота при данных условиях равен
1. 0,05 2. 0,10 3. 0,50 4. 0,90 5. 0,95
28. Из приведенных ниже формул для вычисления момента инерции шара радиуса R относительно оси, проходящей через центр масс, верной является
1.  2.
2. 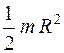 3.
3.  4.
4. 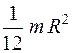 5.
5. 
29. Из приведенных ниже формул к основному закону динамики вращательного движения относятся
1. 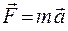 2.
2.  3.
3.  4.
4.  5.
5. 
30. Для расчета момента инерции тела с непрерывным распределением массы применяется формула
1.  2.
2.  3.
3. 
4.  5.
5. 
31. Момент инерции тела относительно любой оси измеряется в
1. кг · м 2. Н · м 3. кг · м2 4. Н · с 5. кг · м/с2
32. Однородное колесо вращается в горизонтальной плоскости по направлению движения часовой стрелки. Вектор момента силы, приложенной по касательной к ободу колеса, направлен
1. по касательной к траектории движения колеса
2. вверх вдоль оси вращения
3. вниз вдоль оси вращения
4. вдоль радиуса в сторону оси вращения
5. вдоль радиуса в сторону, противоположную оси вращения
33. Модуль угловой скорости вращающегося вала, момент инерции которого относительно оси вращения равен 20 кг · м2, изменяется со временем по формуле ω = 1 + 2 t. Момент силы, действующей на вал, равен (Н· м)
1. 10 2. 20 3. 40 4. 60 5. 80
 34. Момент инерции однородного тонкого стержня массы m относительно оси ОО / равен
34. Момент инерции однородного тонкого стержня массы m относительно оси ОО / равен
1. 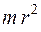 2.
2.  3.
3. 
4.  5.
5. 
35. Момент инерции велосипедного колеса массой m и радиуса R, распределенной по ободу относительно точки его соприкосновения с дорогой, равен
1.  2.
2.  3.
3.  4.
4.  5.
5. 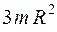
36. Момент инерции шара массой m и радиуса R относительно оси, касательной к поверхности шара, равен
1.  2.
2.  3.
3.  4.
4.  5.
5. 
37. Шар массой m и радиусом R вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид  . Уравнение, определяющее момент сил, действующих на шар, имеет вид
. Уравнение, определяющее момент сил, действующих на шар, имеет вид
1.  2.
2.  3.
3.  4.
4. 
5. 
38. Частота вращения колеса при торможении уменьшилась за 4 с от 300 до 180 об/мин. Момент инерции колеса равен 20 кг · м2. Тормозящий момент, действующий на колесо, равен (Н· м)
1. 10 2. 40 3. 80 4. 400 5. 600
39. Две гири массами m 1 = 3 кг и m 2 = 2 кг соединены нитью, перекинутой через блок массой 1 кг. Блок считать однородным диском. Ускорение, с которым движутся гири, равно (м/с2)
1. 1,8 2. 2,0 3. 3,6 4. 9,1 5. 10,0
40. Наиболее полной формулировкой закона сохранения момента импульса является:
1. в замкнутой системе момент импульса не изменяется со временем
2. полный момент импульса всех тел не изменяется по направлению
3. полный момент импульса всех тел не изменяется по модулю
4. момент импульса системы есть величина постоянная
5. в замкнутой системе момент импульса всех тел не убывает
41. Однородный диск вращается против направления движения часовой стрелки вокруг оси, проходящей через центр масс. Вектор момента импульса направлен
1. вверх вдоль по оси вращения
2. вниз по оси вращения
3. совпадает с направлением вектора скорости движения обода диска
4. вдоль радиуса диска в сторону от оси вращения
5. вдоль радиуса диска в сторону, противоположную оси вращения
42. Человек, стоящий на вращающейся скамье Жуковского, повернул длинный шест из вертикального положения в горизонтальное. Угловая скорость вращения скамьи и момент инерции системы при этом
1. увеличилась, уменьшился
2. уменьшилась, уменьшился
3. не изменилась, уменьшился
4. уменьшилась, увеличился
5. увеличилась, уменьшился
43. Человек, вращающийся на скамье Жуковского, увеличивает момент инерции системы в 4 раза. Угловая скорость вращения скамьи
1. увеличивается в 4 раза
2. уменьшается в 4 раза
3. не изменяется
4. увеличивается в 16 раз
5. уменьшается в 16 раз
44. Шарик, привязанный к концу нити, вращается, опираясь на горизонтальную плоскость. Нить укорачивается в 2 раза. Угловая скорость шарика
1. уменьшается в 2 раза
2. увеличивается в 2 раза
3. уменьшается в 4 раза
4. увеличивается в 4 раза
5. не изменяется
45. Шар массой 5 кг и радиусом 0,5 м вращается вокруг оси, проходящей через центр масс, согласно уравнению  . В момент времени t = 5 с его момент импульса равен (кг · м2/с)
. В момент времени t = 5 с его момент импульса равен (кг · м2/с)
1. 16,25 2. 32,5 3. 65,0 4. 81,25 5. 92,5
 |
46. На рисунке показаны направления угловой скорости и углового ускорения вращающегося диска. Момент импульса диска имеет направление
1. а 2. б 3. в
4. г 5. д
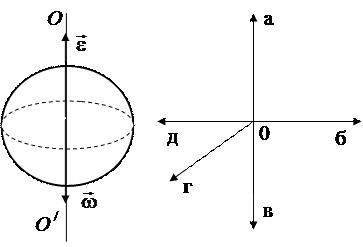 |
47. На рисунке показаны направления угловой скорости и углового ускорения вращающегося шара. Момент силы имеет направление
1. а 2. б 3. в
4. г 5. д
48. Однородный диск массой 2 кг катится без скольжения по горизонтальной поверхности со скоростью 4 м/с. Кинетическая энергия диска равна (Дж)
1. 8 2. 16 3. 24 4. 32 5. 64
49. Карандаш длиной l и массой m, поставленный вертикально, падает на стол, вращаясь относительно точки опоры. Линейная скорость верхнего конца карандаша при падении на стол, равна
1.  2.
2.  3.
3.  4.
4.  5.
5. 
50. Маховик в виде диска массой 80 кг и радиусом 30 см находится в состоянии покоя. Работа, которую нужно совершить, чтобы сообщить маховику частоту 10 с-1, равна (кДж)
1. 0,72 2. 1,13 3. 2,26 4. 7,10 5. 14,2
51. Тело, момент инерции которого 0,04 кг · м2, вращается с постоянным угловым ускорением 5 рад/с2. Работа, совершенная телом при повороте на 5 рад, равна (Дж)
1. 0,2 2. 1,0 3. 2,0 4. 5,0 5. 10,0
52. Работа, совершенная телом при изменении его угловой скорости вращения от 5 рад/с до 10 рад/с, равна 1,5 Дж. Момент инерции тела, равен (кг · м2)
1. 0,04 2. 0,03 3. 0,3 4. 0,6 5. 1,2
3. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
 |
1. На рисунке приведен график зависимости смещения колеблющейся точки от времени, уравнение, его описывающее имеет вид
1.  2.
2.  3.
3. 
4.  5.
5. 
 2. На рисунке приведены графики зависимости смещения колеблющейся точки и амплитуды колебания от времени. Амплитуда колебания меняется по закону
2. На рисунке приведены графики зависимости смещения колеблющейся точки и амплитуды колебания от времени. Амплитуда колебания меняется по закону
1.  2.
2.  3.
3. 
4.  5.
5. 
3. Логарифмический декремент затухания – это физическая величина,
1. показывающая во сколько раз уменьшается амплитуда колебаний за период
2. обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается до нуля
3. обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается в «е» раз
4. обратная промежутку времени, за которое амплитуда колебаний уменьшается в «е» раз
5. обратная промежутку времени, за которое амплитуда колебаний уменьшается до нуля
4. Точка совершает колебание по закону 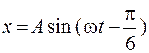 . График зависимости х от времени имеет вид
. График зависимости х от времени имеет вид
 |
1. а 2. б 3. в 4. г 5. д
 5. Точка совершает колебание по закону
5. Точка совершает колебание по закону  . График зависимости скорости
. График зависимости скорости 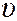 от времени имеет вид
от времени имеет вид
 |
1. а 2. б 3. в 4. г 5. д
6. Точка совершает колебание по закону  . Максимальное ускорение точки равно
. Максимальное ускорение точки равно
1. А 2. А ω 3. А ω2 4. А 2ω2
5. ускорение – постоянная величина
7. Если точка участвует в двух взаимно перпендикулярных колебаниях, происходящих по закону  и
и  , то траектория результирующего колебания может иметь вид
, то траектория результирующего колебания может иметь вид
 | |||||
 |  | ||||
1. а, б, д 2. б, в, д 3. а, б, в, г
4. а, б, в, г, д 5. а, б, в, д
8. Если точка участвует в двух взаимно перпендикулярных колебаниях одинаковой частоты, происходящих по закону  и
и  , то траектория результирующего колебания может иметь вид
, то траектория результирующего колебания может иметь вид

1. а, б, в, г, д 2. в, г, д 3. в, г
4. б, в, г 5. а, в, г
9. Точка совершает колебание по закону  . График зависимости ускорения а от времени имеет вид
. График зависимости ускорения а от времени имеет вид

1. а 2. б 3. в 4. г 5. д
10. Если на расстоянии х 1 и х 2 от положения равновесия частица, совершающая гармонические колебания, имеет скорости равные соответственные υ 1 и υ 2, то амплитуда колебаний равна
1.  2.
2. 
3.  4.
4. 
5. данных для определения амплитуды недостаточно
11. За 10 с амплитуда пружинного маятника массой m = 0,1 кг уменьшилась в «е» раз. Коэффициент затухания β и коэффициент сопротивления r среды равны
1. β = 0,1; r = 0,02 2. β = 1; r = 0,01 3. β = 0,1; r = 0,1 4. β = 0,01; r = 0,04 5. β = 1/2,73; r = 0,02
12. Фигура Лиссажу, образованная при сложениивзаимно перпендикулярных колебаний  и
и  имеет вид
имеет вид

1. а 2. б 3. в 4. г 5. д
13. Период колебаний математического маятника можно уменьшить
1. увеличив амплитуду колебаний
2. увеличив массу маятника
3. удлинив нить подвеса
4. укоротив нить подвеса
5. уменьшив амплитуду колебаний
14. Коэффициент затухания колебаний маятника можно увеличить
1. уменьшив вязкость среды, в которой происходит колебание
2. уменьшив массу колеблющегося тела
3. уменьшив начальную амплитуду колебаний
4. увеличив массу колеблющегося тела
5. уменьшив начальную амплитуду колебаний и вязкость среды
15. Уравнение гармонических колебаний материальной точки 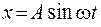 , период колебаний 24 с. Смещение точки от положения равновесия будет равно половине амплитуды через (с)
, период колебаний 24 с. Смещение точки от положения равновесия будет равно половине амплитуды через (с)
1. 6,0 2. 4,0 3. 2,0 4. 1,0 5. 8,0
16. Уравнение гармонического колебания 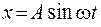 . Зависимость скорости колебания материальной точки от смещения имеет вид
. Зависимость скорости колебания материальной точки от смещения имеет вид
1. 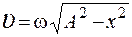 2.
2.  3.
3. 
4.  5.
5. 
17. Амплитуда гармонических колебаний, совершаемых материальной точкой вдоль прямой, равна 0,5 м. Путь, пройденный точкой за период колебаний, равен (м)
1. 2 2. 1,5 3. 1 4. 0,5 5. 0
18. Максимальная скорость гармонического осциллятора 10 см/с, максимальное ускорение 1 м/с2. Период колебаний равен (с)
1. 10 2. 6,28 3. 4 4. 3,14 5. 0,628
19. Небольшое тело на нити совершает колебания как математический маятник. Ускорение тела равно нулю в следующих точках траектории
1. в двух крайних и в положении равновесия
2. только в положении равновесия
3. только в крайних точках
4. зависит от амплитуды
5. ни в одной
20. Небольшое тело на нити совершает колебания как математический маятник. Сила, действующая на тело равна нулю в следующих точках траектории
1. в положении равновесия (нижней точке)
2. в крайних точках
3. и в положении равновесия, и в крайних точках
4. ни в одной точке
5. зависит от массы тела
21. Математический маятник совершает колебания по закону х = 0,004 cos (2 t + 0,8) (м). Длина маятника равна (м)
1. 4 2. 3,25 3. 0,245 4. 2,45 5. 2,05
22. Колебание точки задано уравнением х = 2sin 2,5π (t +0,4). Период колебаний равен (с)
1. 2 2. 1 3. 0,8 4. 0,6 5. 0,4
23. Точка совершает гармонические колебания. Наибольшее смещение точки 10 см, наибольшая скорость 0,2 м/с. Максимальное ускорение точки равно (м/с2)
1. 2 2. 0,2 3. 0,3 4. 0,4 5. 0.04
24. Уравнение колебания материальной точки имеет вид  . Ускорение точки в начальный момент времени определяется соотношением
. Ускорение точки в начальный момент времени определяется соотношением
1.  2.
2.  3.
3. 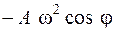
4.  5.
5. 
25. Материальная точка массой 1,25 кг совершает колебания по закону х = cos (2 t + π/4)  (м). Максимальная сила, действующая на точку, равна (Н)
(м). Максимальная сила, действующая на точку, равна (Н)
1. 2,5 2. 5 3. 0,98 4. 3,5 5. 1
26. Тело массой 1 кг совершает колебания вдоль оси х. Его координата изменяется по закону х =2sin 3 t. Потенциальная энергия тела определяется выражением
1.  2.
2.  3.
3. 
4.  5.
5. 
27. Точка совершает гармонические колебания согласно уравнению х = 0,04 sin (π t + 0,3π) (м). Максимальная сила, действующая на точку, равна 1,5 мН. Полная энергия точки (мкДж) равна
1. 60 2. 30 3. 15 4. 12
5. среди ответов нет правильного
28. Материальная точка совершает колебания по закону х = А sin ω t. В некоторый момент времени смещение точки оказалось равным 5 см. Когда фаза увеличилась в 2 раза, смещение стало равным 8 см. Амплитуда колебаний равна (см)
1. 8,33 2. 4,16 3. 3 4. 2,5 5. 2,31
29. Однородный тонкий стержень длиной l совершает колебания около горизонтальной оси, проходящей через конец стержня. Период колебаний равен
1.  2.
2.  3.
3.  4.
4.  5.
5. 
30. Диск радиуса R колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Период его колебаний пропорционален
1.  2.
2.  3.
3.  4.
4.  5.
5. 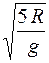
31. Диск радиусом 24 см колеблется около оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Приведенная длина маятника равна (см)
1. 12 2. 14 3. 16 4. 28 5. 36
32. Уравнение колебаний физического маятника массой 0,2 кг и моментом инерции 0,4 кг·м2 определяется выражением х = 2 cos 5 t (м). Расстояние от центра масс до точки подвеса равно (м)
1. 0,4 2. (0,4)0,5 3. 5 4. 4 5. 2
33. Складываются два гармонических колебания одного направления с одинаковыми периодами (1,5 с) и амплитудами А 1= А 2=2 см. Начальные фазы колебаний  . Начальная фаза результирующего колебания равна
. Начальная фаза результирующего колебания равна
1. arctg 2 2. arctg 0,28 3. arctg 3,7 4. π/6 5. 5π/6
34. Уравнение бегущей вдоль оси х волны имеет вид
1. 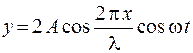 2.
2.  3.
3.  4.
4.  5.
5. 
35. Волна с периодом 1,2 с и амплитудой 2 см распространяется со скоростью 15 м/с. Точка находится на расстоянии 45 м от источника волн. В момент t = 4 с смещение точки равно (м)
1. 0,01 2. 0,06 3. 0,02 4. 0,1 5. 0
36. Уравнение стоячей волны определяется соотношением
1.  2.
2.  3.
3.  4.
4.  5.
5. 
37. Расстояние между первым и третьим узлами в стоячей волне равно 20 см. Длина волны равна (м)
1. 0,8 2. 0,6 3. 0,4 4. 0,2
5. надо знать скорость распространения волны
38. Расстояния между соседними точками, колеблющимися с одинаковыми по величине амплитудами равны 5 см и 15 см. Длина стоячей волны (м)
1. 0,8 2. 0,4 3. 0,2 4. 0,15. 5. данных недостаточно
39. Груз массой 1 кг, подвешенный на пружине, растягивает ее на 20 см. Если оттянуть немного груз и отпустить, то возникнут колебания, период которых равен (с)
1. 0,7 2. 0,9 3. 1,1 4. 1,3 5. 1,8
40. Математический маятник длиной 1 м установлен в лифте, опускающимся вниз с ускорением 2,5 м/с2. Период колебания маятника равен (с)
1. 1,6 2. 1,8 3. 2 4. 2,3
5. данных недостаточно
41. Колебания двух точек, лежащих на луче и отстоящих на расстоянии 2 м друг от друга, если длина волны равна 1 м
1. происходят в одинаковых фазах, 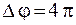
2. происходят в противофазах
3. сдвинуты по фазе на 
4. сдвинуты по фазе на 
5. происходят в одинаковых фазах, 
42. За одно полное колебание амплитуда колебаний математического маятника с логарифмическим декрементом затухания 0,3 уменьшится в
1. «е» раз 2. 1,35 раз 3. 1,22 раза
4. 2 раза 5. 3 раза






