| Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его. |
Для записи условия равновесия системы, состоящей из твёрдых тел, систему разделяют на отдельные части, и записывают уравнения равновесия как для всей системы, так и для её частей [1] . При этом возможны несколько эквивалентных вариантов записи условий равновесия в зависимости от выбора частей системы, для которых записываются уравнения.
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.
Рисунок 1.14.1. Равновесие твердого тела под действием трех сил. При вычислении равнодействующей все силы приводятся к одной точке C На рис. 1.14.1 дан пример равновесия твердого тела под действием трех сил. Точка пересечения O линий действия сил и не совпадает с точкой приложения силы тяжести (центр масс C), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.
Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения.
Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.
Произведение модуля силы на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки (рис. 1.14.2).
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
2. Несвободное твердое тело — это тело, не имеющее возмож%
ность совершать в рассматриваемый момент любые перемещения
в пространстве.
Под связью для твердого тела или материальной точки понимают
материальные объекты, которые ограничивают свободу перемеще%
ния рассматриваемого твердого тела или материальной точки. Акси%
ома связи: всякую связь можно отбросить или заменить силой, реакцией
связей (в простейшем случае) или системой сил (в общем случае). Ре5
акция связи — это сила, с которой связь действует на систему мате%
риальных точек или твердое тело. Сила реакции связи направлена
в сторону, противоположную направлению, в котором связь препят%
ствует перемещению рассматриваемого тела.
3.
Система сходящихся сил. Сходящимися называются силы, линии действия которых пересекаются в одной точке. Равнодействующая сходящихся сил равна геометрической сумме этих сил и приложена в точке их пересечения 
. Равнодействующая может быть найдена геометрич. способом – построением силового (векторного) многоугольника или аналитич. способом, проектируя силы на оси координат. Проекции силы на оси координат (для плоской сист.):Fx=F×cosa; Fy=F×cosb=F×sina; проекция >0, если направление составляющей силы совпадает с направл. оси. Модуль силы: 
;направляющие косинусы: 
разложение силы на составляющи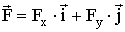е: 
, где 
– орт (единичный вектор) соответствующей оси.
Для пространственной системы: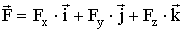 
,
Fx=Fcosa; Fy=Fcosb; Fz=Fcosg; 
; 
.
Проекции равнодействующей системы сходящихся сил на координатные оси равна алгебраическим суммам проекций этих сил на соответствующие оси: Rx=åFix; Ry=åFiy; Rz=åFiz;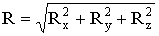 
.
Условия равновесия сист. сходящихся сил: геометрическое: 
аналитические: åFix=0; åFiy=0; åFiz=0. Теорема о трех непараллельных силах: Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
4. Многоугольник сил, ломаная линия, которая строится для определения главного вектора (геометрической суммы) данной системы сил. Чтобы построить Многоугольник сил для системы
| |
| Рис. к ст. Многоугольник сил. |
сил F 1, F 2 ,..., F n (рис., а), надо от произвольной точки а поочерёдно отложить в выбранном масштабе вектор 
, изображающий силу F 1, от его конца отложить вектор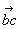 
, изображающий силу F 2, и т. д. и от конца m предпоследней силы отложить вектор 
, изображающий силу F n (рис., б). Фигура abc... mn и называется Многоугольник сил Вектор an, соединяющий в Многоугольник сил начало первой силы с концом последней, изображает геометрическую сумму R данной системы сил. Когда точка n совпадает с а, Многоугольник сил называется замкнутым; в этом случае R = 0. Правило Многоугольник сил может быть получено последовательным применением правила параллелограмма сил.
Построением Многоугольник сил пользуются при графическом решении задач статики для систем сил, расположенных в одной плоскости.
