Таблица 1- Список основных формул кинематики
| Движение | Схема | Уравнение скорости | Уравнен. ускорения | Уравнение пути | Уравнение координаты |
| Равномерное | 
| v=const | a = 0 | S = x- x0 S = vt | x = x0+vt x = x0-vt |
| Равноускоренное | 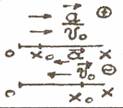
| v=v0+at v=-v0-at | 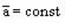
| 
| 
|
| Равнозамед-ленное | 
| v=v0-at v=-v0+at | 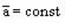
| 
| 
|
| Свободное падение | 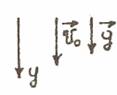
| v=v0+gt | 
| 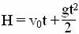
| 
|
| Движение тепа брошенного вертикально вверх | 
| v=v0-gt | 
| 
| 
|
| Движение тела брошенного горизонтально | 
| vx=v0=const vy=gt | ax = 0 ay = g | 
| 
|
| Движение тела брошенного под углом к горизонту | 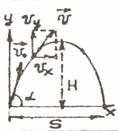
| vx= v0cosα = = const vy = v0sinα-gt | ax = 0 ay = g | 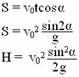
| 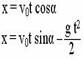
|
| Равномерное окружности | 
| 
| 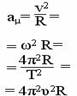
| S = vt Ф = ωR S = φR |
2. II закон Ньютона. Силы в механике.
f=ma.
здесь f — равнодействующая всех сил, действующих на данное тело, m — его масса и а — ускорение, получаемое данным телом под действием силы f.
Эта формула выражает основной закон движения, известный под названием второго закона Ньютона (первый закон — закон инерции; § 31). Второй закон Ньютона можно сформулировать так:
Сила, действующая на тело, равна произведению массы тела на создаваемое этой силой ускорение, причем направления силы и ускорения совпадают.
Формулу можно записать еще и в таком виде:

Систематизированная таблица основных сил, изучаемых в ньютоновской механике
Таблица 2.
| Вид сил | Сила | Формула | Пояснительный рисунок | Особенности | Практическое значение |
| Г Р А В И Т А Ц И О Н Н Ы Е | Всемирного тяготения (закон) | F = G·(m1· m2)/R2 G = 6,67 · 10-11 Нм2/кг2 | 
| а) Сформулирован для точечных тел б)Применяется для однородных сферических тел | Определяют развитие Вселенной, движение планет |
| Сила тяжести | F = G · (m·M3)/R2 или F=mg, где g = G · (M3)/R2 | 

| g -ускорение свободного падения, всегда направлено вниз gэкв.= 9,78 м/с2 gпол.= 9,83 м/с2 gср.шир.=9,81 м/с2 g = G·M3/(R3+h)2- в любой точке над поверхностью Земли | Используют в расчетах движения искусственных спут- ников Земли. Приливы и отливы. Водопа- ды, существование атмосферы. Определение времени и места солнечных и лунных затмений | |
| Э Л Е К Т Р О М А Г Н И Т Н ЫЕ | Сила упругости |
 закон Гука
k- коэффициент жесткости закон Гука
k- коэффициент жесткости
 х- удлинение
х- удлинение
| 
| Всегда направлена в сторону восстановления прежних форм тела; применяется для малых упругих деформаций | Используют в амортизаторах |
| Сила реакции опоры | (дляопоры)
(дляподвеса)

| 
| Направлена перпендикулярно поверхности опоры | Возникают в канатах, тросах, человеческих костях, мышцах | |
| Вес тела | 
| 

| Вес определяется всей совокупностью действий на тело сил и зависит от ускорения, с которыми движется тело | Измерение масс с помощью взвешивания, перегрузки; невесомость | |
| Сила трения | Fтр=μN μ- коэффициент трения | 
| Всегда направлена противоположно вектору скорости. | Препятствует относительному движению соприкасающихся тел, способствует возникновению движения при ходьбе, удерживает в покое различные тела |
Таблица 3 -список основных формул
| Динамика | Работа, мощность, энергия | Жидкости и газы |
1.При 
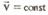 Результирующих всех сил
2.
Результирующих всех сил
2. 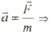
 динамическое уравнение движения динамическое уравнение движения
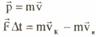 закон изменения импульса или
|| закон Ньютона в общем виде(или закон изменения импульса или
|| закон Ньютона в общем виде(или  )
3. )
3.  Закон сохранения импульса
Закон сохранения импульса
 закон всемирного тяготения
Закон Гука закон всемирного тяготения
Закон Гука

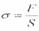 механическое напряжение механическое напряжение
| 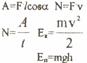 (гравитационная
(гравитационная  ) )
 теорема о связи работы и энергии теорема о связи работы и энергии
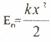 упругих деформаций
Закон сохранения механической энергии упругих деформаций
Закон сохранения механической энергии

|  Давления Давления
 гидростатическое давление гидростатическое давление  Закон Архимеда
Закон Архимеда

 условие неразрывности струи
или условие неразрывности струи
или 
 расход жидкости
Уравнение Бернулли ил закон сохранения энергии в гидромеханике расход жидкости
Уравнение Бернулли ил закон сохранения энергии в гидромеханике

|
3. III закон Ньютона. При каких условиях сохраняется импульс системы тел?
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
4. 
4-6 см. таблицу
7.Пружины, их параллельное и последовательное соединение. Миофибрилла.
При параллельном соединении пружины параллельны, т.е. их концы не связаны с друг другом.
При последовательном - конец одной пружины соединен с началом другой.
Параллельное соединение
При параллельном соединении 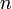 пружин с жёсткостями, равными
пружин с жёсткостями, равными 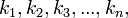 жёсткость системы равна сумме жёсткостей, то есть
жёсткость системы равна сумме жёсткостей, то есть 
Последовательное соединенение
При последовательном соединении 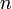 пружин с жёсткостями, равными
пружин с жёсткостями, равными 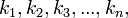 общая жёсткость равна единице, делённой на сумму обратных величин жёсткостей, то есть
общая жёсткость равна единице, делённой на сумму обратных величин жёсткостей, то есть 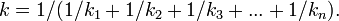
8. Когда можно говорить о силах инерции?
При неравномерном движении системы отсчета (центростремительная сила, приливная, торможения и т.д)
9. Центр инерции системы. Баллистокардиография.
ЦЕНТР ИНЕРЦИИ (центр масс) - геом. точка, положение к-рой характеризует распределение масс в теле или механич. Системе.
Баллистокардиография (греч. ballō бросать + kardia сердце + graphō писать, изображать) — метод графической регистрации реактивных механических движений тела человека, обусловленных сокращениями сердца и перемещением крови в крупных артериях.
10. Работа, энергия, мощность. При каких условиях сохраняется энергия системы? Примеры.
Работу постоянной силы  на перемещение
на перемещение 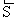 ее точки приложения измеряют произведением:
ее точки приложения измеряют произведением:
A = F S cos a.
Работа по подъему тела массой m в поле тяготения равна:
A = mgh.
Мощность,развиваемая постоянной силой  ,cоставляющей угол a c направлением перемещения, может быть рассчитана по формуле:
,cоставляющей угол a c направлением перемещения, может быть рассчитана по формуле:
N =A/t =Fvcos a.
Кинетическая энергия тела:
T = mv2/2.
Энергия упруго деформированного тела:
П = kx2/2.
11. Чему равна кинетическая энергия тела? В каких единицах она измеряется, и как можно ее
изменить?
Кинетическая энергия тела:
T = mv2/2.
12.Гравитационная и упругая потенциальная энергия. В каких единицах она измеряется, и
как можно ее изменить?


13. Чему равен импульс тела?
 . 1 кг*м/с
. 1 кг*м/с
14. Момент инерции и энергия вращения тела. Движение конечностей тела человека.
Моменты инерции симметричных тел смотри рис. Ниже

15. Момент силы. Рычаги. Виды рычагов в опорно-двигательном аппарате человека.
M=Fl-момент силы. Рычаг-тело способное вращаться вокруг неподвижной опоры
16. Уравнение моментов для вращательного движения (II закон Ньютона)
Jε = M. из
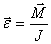
|
Это выражение представляет собой аналог второго закона Ньютона для вращательного движения, из которого следует, что угловое ускорение твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции относительно этой оси.
17. Что такое момент импульса тела? При каком условии сохраняется момент импульса
системы?
L=rmv=rp
18. Виды деформаций. Модуль Юнга. Кривая деформации и разрушение тел. Жевание
коренными зубами и резцами.
Основными деформациями являются деформации растяжения (сжатия) и сдвига. При деформации изгиба происходит неоднородное растяжение и сжатие, а при деформации кручения – неоднородный сдвиг.
| Вид деформации | Признаки |
| Растяжения | увеличивается расстояние между молекулярными слоями. |
| Сжатия | уменьшается расстояние между молекулярными слоями. |
| Кручения | поворот одних молекулярных слоев относительно других. |
| Изгиба | одни молекулярные слои растягиваются, а другие сжимаются или растягиваются, но меньше первых. |
| Сдвига | одни слои молекул сдвигаются относительно других. |
| Упругая | после прекращения воздействия тело полностью вос-станавливает первоначальную форму и размеры. |
| Пластичная | после прекращения воздействия тело не восстанавливает первоначальную форму или размеры. |
Закон Гука
Связь между силой упругости и упругой деформацией тела (сжатия) имеет вид
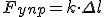
Состояние упруго деформированного тела характеризуют величиной σ, называемой механическим напряжением.
Механическое напряжение σ равно отношению модуля силы упругости F упр к площади поперечного сечения тела S:
 .
.
Измеряется механическое напряжение в Па: [ σ ] = Н/м2 = Па.
Наблюдения показывают, что при небольших деформациях механическое напряжение σ пропорционально относительному удлинению ε:
 . (2)
. (2)
Эта формула является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным.
Коэффициент пропорциональности Е в законе Гука называется модулем упругости (модулем Юнга). Экспериментально установлено, что
модуль Юнга численно равен такому механическому напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза.
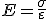 . Измеряется модуль Юнга в Па: [ E ] = Па/1 = Па.
. Измеряется модуль Юнга в Па: [ E ] = Па/1 = Па.
19. Уравнение гармонических колебаний и их основные характеристики.
Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или
 ,
,
где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд  — полная фаза колебаний,
— полная фаза колебаний,  — начальная фаза колебаний.
— начальная фаза колебаний.
20. При каких условиях возникают гармонические колебания? Маятники.
При выведении системы из равновесия
21. От чего зависят период, частота, амплитуда и начальная фаза колебаний маятника?
От начальных условий
22. Почему период колебаний математического маятника не зависит от массы тела,
подвешенного на нити? При каких условиях период колебаний маятника не зависит от
амплитуды?
23.Превращения энергии при гармонических колебаниях? От чего зависит полная энергия
этих колебаний? Ep в Ek
24. Затухание колебаний. Показатель затухания
Для характеристики интенсивности затухания вводят понятие логарифмического декремента затухания Это величина d, равная:
d = ln(Аn /An+1) или
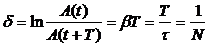 - логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в e раз. Соответственно, exp(bT) - просто декремент затухания.
- логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в e раз. Соответственно, exp(bT) - просто декремент затухания.
25. Вынужденные колебания. Резонанс.
Вынужденными называются колебания, которые система совершает под действием внешней силы.






