ОПРЕДЕЛЕНИЕ МОДУЛЯ КРУЧЕНИЯ СТЕРЖНЕЙ
СТАТИЧЕСКИМ И ДИНАМИЧЕСКИМ МЕТОДАМИ.
Цель работы: ознакомиться с видами деформации твердого тела, опытным путем определить модуль кручения и модуль сдвига металлического стержня и проволоки.
Введение.
Все реальные тела деформируемы. Под действием приложенных сил они меняют свою форму или объем.
Для идеально упругих тел существует однозначная зависимость между действующими силами и вызываемыми ими деформациями. Упругие деформации, подчиняющиеся закону Гука, называют малыми. Согласно этому закону деформации пропорциональны силам, их вызывающим.Деформации разделяют на однородные (растяжение, сжатие) и неоднородные (кручение, изгиб).Если один из концов длинного однородного стержня закрепить, к другому приложить закручивающий момент сил М, то этот конец повернётся на угол, причём, согласно закону Гука:
 (1)
(1)
Постоянная величина f носит название модуля кручения. Модуль кручения связан с модулем сдвига
материала стержня G соотношением:
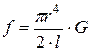 (2)
(2)
где r - радиус, а L - длина стержня (1.37 m).
Отметим, что простая линейная зависимость между величинами М и φ даваемая формулой (1), имеет место только при сравнительно небольших значениях М В общем случае зависимость φ =f (М) может быть не только нелинейной, но и неоднозначной. Соотношение


указывает на два возможных метода экспериментального определения модуля сдвига:
статический – путем путем измерения момента внешних сил(численно равного моменту сил упругости) и соответствующего угла закручивания;
динамический – путем измерения периода Т крутильных свободных колебаний тела, подвешенного на исследуемой проволоке.
Определение модуля кручения стержня
Статическим методом
Принадлежности: исследуемый стержень, газовый лазер со шкалой, рулетка, микрометр, набор грузов.

Рис. 1.
Экспериментальная установка изображена на рис.1.Верхний конец вертикального стержня С жёстко закреплён на стойке, а нижний соеденён с диском Д. Момент М,закручивающий стержень, создают две навитые на диск и перекинутые через блоки Б нити, к концам которых подвешиваются одинаковые грузы Г. Диск снабжён зеркальцем З. Для определения угла закру чивания стержня надо луч лазера направить на зеркальце и добиться того, чтобы отражение луча попало на шкалу. Наблюдая за смещением видимого луча при закручивании стержня, можно определить угол закручивания по формуле:
 (3)
(3)
где X - величина смещения луча по шкале,
l - расстояние от зеркальца до шкалы.
Момент сил, действующий на стержень, определяется как
М = mgR, (4)
где m - масса груза,
R - радиус диска.
Измерения
1. Установите газовый лазер таким образом, чтобы луч отражался от зеркальца З и попадал на шкалу.
2. Подвешивая грузы, увеличив нагрузку на нитях Н, снимите зависимость = f (М). Проделайте эксперимент в обратном порядке, постепенно уменьшая величину закручивающегося момента. Весь комплекс измерений повторите не менее трёх раз.
3. Результаты эксперимента изобразите графически в координатах (φ,М). По коэффициенту наклона прямой определите величину. Оцените допущенную при этом погрешность.
4. Используя формулу (2), вычислите модуль сдвига G. Сверьте полученное таким образом значение с табличным.
Результаты измерений занесите в таблицу 1.
| N | m | M | φ1 | φ2 | φср |
∆j= ∆m= ∆M=
Определение модуля сдвига
при помощи крутильных колебаний.
Принадлежности: проволока из исследуемого материала, грузы, секундомер, микрометр, масштабная линейка.
Экспериментальная установка состоит из длинной вертикально висячей проволоки, к нижнему концу которой прикреплена горизонтальная платформа с четырьмя симметрично расположенными грузами. Их положение на платформе можно фиксировать. Верхний конец проволоки будет зажат в цангу и при помощи специального приспособления вместе с цангой может поворачиваться вокруг вертикальной оси. Таким образом в системе можно возбуждать крутильные колебания. Запишем для этого случая уравнение движения:
 (5)
(5)
Здесь М - момент сил, обязанный своим происхождением упругим деформациям,
J - момент инерции платформы с грузами,
φ- угол поворота платформы.
Если амплитуда колебаний невелика, то для определения момента сил М можно воспользоваться законом Гука в форме (1). Момент М в этом случае вызван деформацией проволоки и стремится уменьшить, а не увеличить угол φ. В формуле (1) необходимо, поэтому переменить знак.
После подстановки (1) формула (5) приобретает вид:

 (6)
(6)
Решением (6) является
 (7)
(7)
где амплитуда φ и фаза Ө определяется начальными условиями.
Таким образом, период колебаний Т равен:
 (8)
(8)
Следует заметить, что последняя формула получена для не затухающих колебаний, в то время, как на самом деле колебания платформы всегда затухают. Если, однако, затухание не велико, т.е. изменение амплитуды колебаний за период много меньше самой амплитуды, то формулой (6) можно пользоваться. Критерием её применимости служит неравенство:
n >> 1, (9)
где n - число полных колебаний, после которого амплитуда уменьшается в 2-3 раза.
Отметим, что период Т при малых не зависит от амплитуды. Однако при больших амплитудах закон Гука нарушается и такая зависимость может проявиться. Таким образом, вторым условием применимости описываемого метода является соблюдение равенства:
Т = const (10)
Динамический метод не требует точной аппаратуры для измерения углов и момента сил и находит широкое применение для экспериментального определения модуля сдвига.
Измерения
1. Прежде всего установите диапазон амплитуд, в котором выполняется условие (10). Для этого укрепите грузы на некотором расстояние от проволоки и возбудите в системе крутильные колебания. Измеряя время нескольких (не менее 10-ти) полных колебаний, найдите период Т1. Уменьшив амплитуду вдвое, тем же способом определить период Т2. Если Т1=Т2 то для проведения измерений можно выбрать любую амплитуду не
больше первой. Если же окажется, что Т1 > Т2, то амплитуду необходимо уменьшить до такого значения φ, начиная с которого для всех φ0 <φ будет справедливо равенство Т1= Т2
2. Проверьте справедливость неравенства (9).
3. Установив грузы так, чтобы их центры масс находились на некотором расстоянии L от оси системы, измерьте период, как описано выше. Если J - момент инерции платформы без грузов, а J1- момент инерции грузов, то очевидно, что
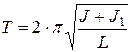 (11)
(11)
Установив грузы на расстоянии L2 от оси, аналогично получим:
 (12)
(12)

 (13)
(13)
где m - суммарная масса грузов.
4.Зная f, найдите значение модуля сдвига G по формуле (2) и оцените допущенную при этом погрешность. Результаты измерений занесите в таблицу 2.
Таблица 2.
| N | m | L1 | L2 | t1 | t2 | n | T1 | T2 | r | f | G |
∆m =, ∆L =, ∆T =
контрольные вопросы
1. Виды деформаций твёрдых тел.
2. Нормальные и касательные (тангенциальные) напряжения.
3. Закон Гука для нормальных и касательных (тангенциальных) напряжений.
4. Что такое модуль Юнга и модуль сдвига?
5. Что такое модуль кручения?
6. Как распределены упругие деформации по длине однородного стержня в статическом режиме нагружения?
7. Какие измерения вносят максимальную погрешность при определении модуля сдвига (кручения) в статическом методе?
8. Чем определяется погрешность в определении угла поворота зеркала?
Составители:
Алексеев В. П.
Неменко Е. О.






