Определение отношения удельной теплоемкости газа

ПРИ ПОСТОЯННОМ ДАВЛЕНИИ К УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ

ПРИ ПОСТОЯННОМ ОБЪЕМЕ МЕТОДОМ КЛЕМАНА И ДЕЗОРМА

Цель работы: Определение отношения теплоемкостей для воздуха, экспериментальное изучение адиабатического процесса.

Приборы и принадлежности:1. Колба.

2.Водяной манометр.

3.Насос.

8.1.Теоретическое введение

Величина теплоемкости газа зависит от вида процесса, при котором происходит его нагревание. Теплоемкость при постоянном давлении С_р больше, чем при постоянном объеме С_V, т.к. при постоянном давлении тепло затрачивается не только на повышение температуры газа, но и на работу по его расширению. Отношение этих теплоемкостей есть величина постоянная для данного газа

(8.1)

и может быть определена из адиабатического процесса.

Адиабатическим называется процесс, происходящий без теплообмена с окружающей средой. На практике такой процесс можно осуществить путем быстрого расширения газа. При адиабатическом расширении работа совершается за счет уменьшении внутренней энергии газа, что приводит к понижению его температуры. Адиабатическое сжатие осуществляется внешними силами, т.е. над газом совершается работа без теплообмена с окружающей средой и температура газа повышается. Давление и объем при адиабатическом процессе связаны уравнением Пуассона

(8.2)

В данной работе адиабатический процесс воспроизводится на приборе, изображенном на рис.1. Колба А сообщается с атмосферой через трубку В, а посредством трубки С с водяным манометром М. Трубка Д имеет кран К₂ и соединяется с насосом.

В колбу нагнетается некоторое количество воздуха и давление будет

где H – атмосферное давление;

h₁ – избыточное давление, измеряемое манометром М.

Таким образом, начальное состояние газа характеризуется параметрами T₁, P₁, V₁, h₁, которому на диаграмме состояний соответствует точка 1 (см. рис.2).

Для адиабатического расширения газа открывается на мгновение кран К₁, в результате давление внутри колбы выравнивается с атмосферным. На диаграмме состояний этот процесс изображен отрезком адиабаты 1-2. Газ перешел в состояние 2 с параметрами: T₂, P₂, V₂, где

Так как кран К₁ закрыт, то воздух в колбе, охладившийся при расширении, будет нагреваться изохорически, т.е. при постоянном объеме он перейдет в состояние 3 по изохоре 2-3. При этом температура его возрастает до первоначальной Т₁, а давление – на некоторую величину, соответствующую поднятию столбика воды в манометре h₂. Состояние 3 характеризуется параметрами:

Для определения величины γ составим два уравнение:

Уравнение адиабаты 1-2 (8.3)

или (8.4)

и уравнение изотермы, т.к. состояния 1 и 3 имеют одинаковую температуру

(8.5)

Учитывая, что V₃ = V₂, имеем

(8.6)

Сравнивая (8.4) и (8.6), находим

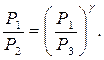(8.7)

Логарифмируя (8.7), выразим γ через h₁ и h₂

(8.8)

Величины 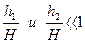, поэтому применяя к (8.8) разложение

(8.9)

ограничиваемся первым членом ряда. Тогда

(8.10)

8.2.Порядок выполнения работы

8.2.1.Откройте кран К₂ и с помощью насоса накачайте в колбу некоторое количество воздуха так, чтобы разностей уровней в манометре была около 20 см. Накачивать воздух следует осторожно, т.к. при слишком большой подаче воздуха может произойти выброс

жидкости из манометра.

Рис.1 Рис.2

8.2.2.Закройте кран К₂ и наблюдайте за манометром. При сжатии газ немного нагреется, а его охлаждение ведет к уменьшению давления, что и будет наблюдаться на манометре. Убедитесь, что разность уровней в манометре не изменяется, и запишите разность высот h₁. Отсчеты берите по вогнутой части мениска.

8.2.3.Откройте кран К₁, выровняйте давление внутри колбы с атмосферным и быстро закройте его.

8.2.4.Наблюдайте за манометром до тех пор, пока давление не перестанет повышаться. Запишите разность уровней h₂ и найдите γ.

8.2.5.Задавая различные величины h₁, повторите опыт не менее 5 раз. Данные запишите в табл.1.

8.2.6.Найдите абсолютную и относительную ошибки и представьте результат в виде

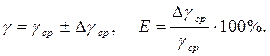
Таблица 1

N п/п h₁, мм h₂, мм γ Δγ Примечания

Сред.

8.3.Контрольные вопросы

8.3.1.Дайте определение теплоемкости.

8.3.2.Что называется удельной теплоемкостью, молярной? Как они связаны?

8.3.3.Какая теплоемкость больше, при постоянном давлении или при постоянном объеме? Почему?

8.3.4.Охарактеризуйте процессы: изобарический, изохорический, изотермический.

8.3.5.какая величина остается постоянной при адиабатическом процессе?

8.3.6.Сформулируйте законы, которым подчиняется газ при изобарическом, изохорическом, изотермическом и адиабатическом процессах. Запишите их.

8.3.7.Считая воздух двухатомным и идеальным газом, определите для него значение γ по числу степеней свободы.

Литература

1. Путилов К.А. «Курс физики», т.1,М.,Физматгиз, 1963.

2. Зисман Г.А., Тодес О.М. «Курс общей физики», т.1, М., «Наука», 1974.

3. Савельев И.В. «Курс общей физики», т.1, М., «Наука», 1973.

4. Физический практикум под редакцией профессора Ивероновой, М., «Наука», 1976.

ЛАБОРАТОРНАЯ РАБОТА № 9

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ

Цель работы: Экспериментальное определение коэффициента вязкости воды при комнатной температуре.

Приборы и принадлежности:

1. Прибор для определения вязкости.

2. Отсчетный микроскоп.

3. Секундомер.

4. Стакан.

5. Мензурка.

6. Подставка для капиллярной трубки.

9.1.Теоретическое введение

Всем реальным жидкостям и газам в большей или меньшей степени присуща вязкость или внутреннее трение. С точки зрения молекулярно-кинетической теории вещества причиной внутреннего трения является наложение хаотического теплового движения молекул и упорядоченного движения слоев газа или жидкости. Благодаря тепловому движению, молекулы переходят из слоя 2 (рис.1), движущегося со скоростью u₂, в слой 1, движущейся со скоростью u₁. При этом молекулы из слоя 2 переносят в слой 1 импульсы mu₂ своего упорядоченного движения, а молекулы слоя 1 – в слой 2 импульсы mu₁. Так как u₁ < u₂, то в результате таких переходов слой 1 будет ускоряться, а слой 2 тормозится. Таким образом, физическая природа внутреннего трения состоит в переносе количества движения из одного слоя в другой молекулами, имеющими различные скорости упорядоченного движения. Максимальная скорость направленного движения жидкости устанавливается по оси трубки, уменьшаясь до нуля около ее стенок. Изменение скорости на единицу толщины слоя называется градиентом скорости. Сила внутреннего трения f между слоями жидкости прямо пропорциональна градиенту скорости и площади соприкасающихся слоев S.

(9.1)

где η – коэффициент внутреннего трения или вязкости.

Коэффициент внутреннего трения численно равен силе, действующей между слоями площади при градиенте скорости, равном единице.

Коэффициент вязкости зависит от молекулярного строения жидкости или газа, существенно изменяясь с температурой.

У жидкостей коэффициент вязкости сильно уменьшается с температурой, у газов наоборот возрастает.

Жидкости с большим коэффициентом вязкости создают большое трение частей машин и механизмов, а с малым - вытекают, что приводит к отсутствию смазки. Поэтому на практике необходимо измерять коэффициент вязкости экспериментально.

Для вывода расчетной формулы η рассмотрим цилиндрический слой жидкости радиуса r и длины l (рис.1).

Рис.1

Поверхность этого слоя

(9.2)

А сила трения

(9.3)

Эта сила направлена против движения жидкости и при равномерном движении должна уравновешиваться силой, оказывающей давление на площадь выбранного слоя. Следовательно,

(9.4)

Разделяя переменные и интегрируя, получим

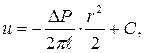(9.5)

где С – постоянная интегрирования, определяемая из условия нормировки r = R, u = 0.

(9.6)

С учетом (9.6)

(9.7)

Таким образом, распределение скоростей по сечению трубки подчиняется параболическому закону.

Определим объем жидкости, протекающей через трубку в течение времени t

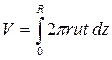. (9.8)

Учитывая (9.7) и интегрируя, получим

(9.9)

Отсюда находим формулу для определения коэффициента вязкости

(9.10)

Для определения η используется прибор Пуазейля (рис.2), который состоит из сосуда А, заполненного исследуемой жидкостью и помещенного на столик К. Высота столика может меняться. Сосуд А соединяется с капиллярной трубкой СD, по которой жидкость стекает в стакан М. Трубка CD может находится на подставке N в положении 1 или 2.

рис.2

Перед опытом сосуд А заполняется исследуемой жидкостью до уровня h’ конец трубки СD в положении 2 оказывается на высоте h’ Жидкость стекает в сосуд М и за время t вытечет объем жидкости V. После опыта уровень жидкости в сосуде А понизится до h”.

Перепад давлений, таким образом, составляет

(9.11)

Объем вытекшей жидкости определяется с помощью мензурки, длина трубки – линейкой, а диаметр – с помощью микроскопа «Мир – 1».

Отсчетный микроскоп применяется для точного измерения небольших длин порядка нескольких миллиметров. Микроскоп имеет выдвижной тубус, на котором нанесена шкала от 130 до 200 мм. Меняя длину тубуса, выбирают из табл.1 соответствующий коэффициент увеличения. И так, что измеряемая величина

D = k∙n, (9.12)

где n – число делений, отсчитанное в поле зрения микроскопа.

Таблица 1

Длина тубуса, мм

k, см/дел 0,0058 0,0058 0,0049 0,0045 0,0041 0,0038 0,0036

Небольшой образец капиллярной трубки вставлен в пробку, которая помещается на предметный столик микроскопа. С помощью микрометрического винта добиваются четкого изображения среза. Так как диаметр трубки в различных направлениях неодинаков, то рекомендуется произвести несколько измерений, каждый раз поворачивая образец.

9.2.Порядок выполнения работы

9.2.1.Измерьте диаметр трубки в различных направлениях не менее трех раз, результаты измерений занесите в табл.2.

9.2.2.Измерьте высоту h’ уровня жидкости в сосуде А.

9.2.3.Большим пальцем правой руки закройте отверстие трубки CD и опустите ее в положение 2, дайте возможность жидкости вытекать в слегка отодвинутый от конца трубки стакан М, измерьте высоту h от середины струи до стола.

9.2.4.Быстро перекройте струю пальцем, воду вылейте в сосуд А (левой рукой).

9.2.5.Освободите отверстие трубки CD и одновременно пустите секундомер, взятый в левую руку. Когда сосуд М заполнится приблизительно на три четверти объема, перекройте трубку и поднимите в положение 1.

9.2.6.Измерьте высоту уровня воды в сосуде А после опыта.

9.2.7.Повторите опыт три раза и результат представьте в виде

Таблица 2

№ пп n D, см h’, см h, см t, с h”, см V, см³ ∆ρ, дин/см² η, г/см∙с ∆η, г/см∙с

Ср.

9.3.Контрольные вопросы

9.3.1.Какова природа внутреннего трения?

9.3.2.Дайте физический смысл коэффициента вязкости.

9.3.3.Как изменяется коэффициент вязкости от температуры?

9.3.4.Какие явления принято называть явлениями переноса? Почему их так называют?

Литература

1. Путилов К.А. Курс физики, т.1, Физматгиз, 1963.

2. Тодес О.М. и Зисман Г.А. Курс общей физики, т.1, М., «Наука», 1974.

3. Савельев И.В. Курс общей физики, т.1, М., «Наука», 1973.

4. Физический практикум под редакцией профессора Ивероновой, М., «Наука», 1967.

ЛАБОРАТОРНАЯ РАБОТА № 10

ИЗМЕНЕНИЕ ЭНТРОПИИ В ПРОЦЕССАХ ТЕПЛООБМЕНА

Цель работы: Экспериментальное определение изменения энтропии в процессах теплообмена между телами.

Приборы и принадлежности:

1. Калориметр.

2. Технические весы.

3. Разновес.

4. Термометры.

5. Плитка.

6. Химический стакан.

7. Мешалка.

8. Набор испытуемых тел.

10.1. Теоретическое введение

Первое начало термодинамики или закон сохранения энергии для термодинамических систем не исключает возможности процессов, которые в действительности не реализуются. Например, с помощью воздуха холодного помещения нельзя увеличить температуру горячей батареи водяного отопления, хотя такой процесс не противоречил бы первому началу термодинамики. Действительно, с точки зрения первого начала термодинамики батарея получит столько тепла, насколько уменьшится внутренняя энергия воздуха. Но самопроизвольно такой процесс не пройдет.

На направленность реально протекающих процессов указывает второе начало термодинамики: возможны процессы, единственным результатом которых являлся бы переход тепла от тел, менее нагретых к более нагретым.

Второе начало термодинамики может быть сформулировано также следующим образом: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от тел некоторого количества тепла и превращение этого тепла полностью в работу.

Третья формулировка дает математическую интерпретацию второго начала термодинамики на основе некоторой функции состояния тел, называемой энтропией S. Приращение энтропии определяется приращенным теплом . Приведенным теплом называется отношение теплоты, полученной системой тел, к температуре, при которой эта передача осуществляется. Итак, в изолированных системах все процессы самопроизвольно могут протекать в направлении , где знак равенства справедлив для обратимых процессов, а для необратимых процессов – приращение энтропии всегда больше нуля.

Процесс называется обратимым, если система может вернуться в первоначальное состояние, пройдя в обратном порядке все промежуточные состояния, причем после окончания процесса не должно остаться никаких изменений в окружающей среде (процесс обратим даже, если обратный ему процесс не осуществлен, а только в принципе возможен). Реальные процессы связаны с обратимыми потерями. Процесс выравнивания температур тем ближе к обратному (dS – оставаясь всегда положительным, уменьшается), чем быстрее во всем объеме тел исчезают местные, локальные неоднородности температур соприкасающихся тел, рассчитанная на единицу объема, обратно пропорциональна теплоемкости тела.

Если в калориметр, содержащий определенное количество воды при заданной температуре, опустить нагретое тело, то произойдет теплообмен и установится общая температура. Если повторить опыт с теми же исходными данными, уменьшив теплоемкость погружаемого тела, то получим более близкий к обратному процесс. Степень его обратимости в изолированной системе определяется на основе измерения приращения энтропии dS.

Изменение энтропии системы запишем из следующих соображений: энтропия системы в начальном состоянии S₀ (воде, калориметр, термометр с начальной температурой Т₀ и нагретое до температуры Т₁ тело), а затем в конечном – S (тело погрузили в калориметр с водой и система приняла температуру Т, где T₀ < T < T₁). Тогда ∆S = S – S₀ и энтропия любого тела с температурой Т

(10.1)

где dQ = mcdT – количество тепла, которое пошло на нагревание тела массой m, причем удельная теплоемкость тела С – некоторая функция температуры.

Итак, энтропия в начальном состоянии равна сумме энтропией всех тел, составляющих систему. Непосредственно перед опытом

(10.2)

где энтропия воды;

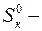энтропия калориметра;

энтропия термометра;

энтропия тела.

В начальном состоянии с учетом (10.1)

(10.3)

В конечном состоянии энтропия системы

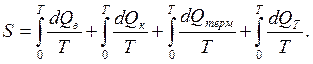(10.4)

По второму закону термодинамики при выравнивании температур в системе энтропия возрастает, т.е. dS > 0. Таким образом,

(10.5)

где dQ – для каждого тела определяется его теплоемкостью.

Для металлов теплоемкость растет по кубическому закону до температур порядка 150 К, затем медленнее, а при температурах 250 – 270 К практически постоянна. При дальнейшем возрастании температуры теплоемкость твердых тел очень медленно растет, меняясь в четвертом знаке после запятой. Поэтому в работе можно принять С_К, С_ТЕРМ, С_Т постоянными (табл.1).

Теплоемкость жидкостей в большинстве случаев выражается так: С = С₀ + αТ, где t – температура по шкале Цельсия, имеет порядок 10^-3. Поэтому при нагревании воды в процессе опыта на несколько градусов, можно не учитывать зависимость ее теплоемкости от температуры (табл.1).

С учетом вышесказанного имеем

(10.6)

Таблица 1

Вещество Вода Калориметр Термометр Латунь Сталь Медь Олово Свинец

С (Дж/кг·К)

Произведя опыт с различными телами, вычислите изменение энтропии ∆S и удостоверьтесь, что второй закон термодинамики выполняется, т.е. в процессе выравнивания температур энтропия возрастает (∆S >0).

10.2.Порядок выполнения работы

10.2.1.Взвесьте калориметрический стакан и налейте в него 150 – 200 см³ воды.

10.2.2.Взвесьте стакан с водой, определите массу воды. (Данные занесите в табл.2).

10.2.3.Включите плитку с химическим стаканом. В стакан опустите тело и термометр.

10.2.4.Поместите калориметр подальше от нагревателя и определите температуру воды Т₀ в калориметре.

10.2.5.После того, как термометр в химическом стакане покажет температуру 65 ⁰С, плитку выключите, и следите за ходом температуры. Как только рост температуры прекратиться, отметьте температуру Т и быстро переносите тело в калориметр, предварительно пододвинув его к нагревателю.

10.2.6.Калориметр закройте, отодвиньте от нагревателя и следите за ростом температуры.

10.2.7.Зафиксируйте максимальное значение температуры Т в калориметре и найдите ∆S.

Таблица 2

№ m_ТЕРМ, кг m_в, кг m_К, кг m_T, кг T₀, K T₁, K T, K S₀, Дж/К S, Дж/К ∆S, Дж/К

Примечания:

1. Важно, чтобы в каждом опыте количество и начальная температура воды в калориметре были одинаковыми.

2. Мешалкой пользуйтесь только в конце процесса роста температуры, делая не более 3 – 5 помешиваний.

3. Натуральные логарифмы вычислите с точностью до четырех знаков, пользуясь таблицами.

10.3.Контрольные вопросы

10.3.1.Сформулируйте первое и второе начала термодинамики.

10.3.2.Какое начало термодинамики говорит о направлении процессов, протекающих вокруг нас?

10.3.3.Что такое энтропия? В каких единицах она измеряется?

10.3.4.Дайте определение обратимого и необратимого процессов.

10.3.5.что является мерой обратимости данного реального процесса? В каком случае процесс ближе к обратимому?

Литература

1. Путилов К.А. «Курс физики», т.1, М., 1963.

2. Зисман Г.А., Тодес О.М. «Курс общей физики», т.1, М., 1974.

3. «Физический практикум» под редакцией проф. Ивероновой, «Наука», М., 1976.

ЛАБОРАТОРНАЯ РАБОТА № 11

ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА

И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА

Цель работы: Определение средней длины пробега молекул и эффективного диаметра молекул воздуха.

Приборы и принадлежности:

1. Сосуд с краном и капилляром.

2. Секундомер.

3. Весы с разновесом.

4. Линейка.

5. Стакан.

11.1.Теоретическое введение

Хаотическое движение молекул, согласно молекулярно – кинетической теории, является физической причиной наблюдаемых в газах и жидкостях явлений переноса: диффузии (перенос массы при выравнивании концентраций), теплопроводности (перенос энергии при выравнивании температур), вязкости (перенос импульса).

Хотя скорости молекул могут достигать нескольких сотен метров в секунду, процессы переноса совершаются сравнительно медленно. Причиной этому является столкновение между молекулами, в результате которых их движение происходит по ломаной линии, а не прямолинейно.

Расстояние, пройденное молекулой между двумя последовательными столкновениями, называется длиной свободного пробега (λ). Длина свободного пробега – случайная величина.

Каждый раз молекула проходит различные расстояния между двумя столкновениями, поэтому целесообразно рассчитывать среднюю длину свободного пробега < λ >.

Известно, что силы межмолекулярного взаимодействия становятся заметными лишь на достаточно малых расстояниях, поэтому путь между столкновениями пройдет молекула в равномерном и прямолинейном движении.

Отклонение молекул от прямолинейных траекторий происходит при столкновениях. Минимальное расстояние между центрами двух молекул при их столкновении называется эффективным диаметром молекул d.

В данной работе путем коэффициента внутреннего трения проводится определение длины свободного пробега и эффективного диаметра молекул воздуха.

Для определения < λ > и d используется установка, изображенная на рис.1. Сосуд на три четверти заполнен водой. Сверху закрыт пробкой, в которую вставлен капилляр.

Если снизу сосуда открыть кран, то вода будет выливаться из сосуда непрерывной струей, а потом сериями отдельных капель. В то же время, через верхний капилляр в сосуд будет насасываться воздух. Так как капилляр очень узок и воздух просачивается очень медленно, то его концы будут находиться под разным давлением: верхний – под атмосферным, нижний – меньше атмосферного. Объем газа V, прошедшего сквозь узкую трубку с круглым внутренним сечением за время τ определяется формулой Пуазейля

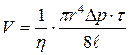, (11.1)

где r и ℓ - соответственно радиус и длина капиллярной трубки;

∆р – разность давлений на концах капилляра, которая обуславливает течение газа (или жидкостей).

Из уравнения (11.1) коэффициент внутреннего трения (вязкости) выразится соотношением:

. (11.2)

Здесь все величины доступны непосредственному измерению.

С другой стороны, молекулярно-кинетическая теория устанавливает связь между коэффициентами вязкости, средней длиной свободного пробега <λ> и средней арифметической скоростью их движения (<υ>)

, (11.3)

где ρ – плотность газа.

Средняя скорость молекул газа может быть найдена по формуле молекулярно-кинетической теории

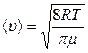, (11.4)

где R – универсальная газовая постоянная, равная 8,31∙10³ Дж/кмоль;

Т – абсолютная температура;

μ – масса одного моля газа (для воздуха ≈ 29 кг/кмоль).

Плотность газа можно найти из уравнения Менделеева - Клапейрона

. (11.5)

Откуда

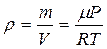, (11.6)

где Р – давление газа.

Подставляя формулы (11.2), (11.4), (11.6) в (11.3) и производя элементарные преобразования, получим формулу для определения <λ>

. (11.7)

Средняя длина свободного пробега связана с эффективным диаметром молекулы (d) соотношением

, (11.8)

где n – число молекул в единице объема, которое определяем из уравнения состояния идеального газа

, (11.9)

где n₀ – число Лошмидта, т.е. число молекул в единице объема (1 см³) при нормальных условиях (Р₀ = 1,013∙10⁵ Н/м², n₀ = 2,69∙10²⁵ м^-3, Т₀ = 273 К).

Применяя формулы (11.8) и (11.9), получаем выражение для эффективного диаметра молекул газа

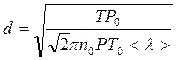. (11.10)

11.2Порядок выполнения работы

11.2.1Открыть кран и подождать, когда вода начнет вытекать из сосуда каплями, подставить предварительно взвешенный стаканчик.

11.2.2.Когда в стаканчике воды будет около 50 – 70 см³ перекрыть кран, записать время истечения жидкости и сделать отсчет по шкале нового уровня воды в сосуде (h₂).

11.2.3.По весу стаканчика с водой определить ее объем, который будет равен объему воздуха, вошедшего в сосуд через капилляр.

11.2.4.Средняя разность давлений, под действием которой воздух входит в сосуд, может быть найдена по формуле

.

11.2.5.Температуру определить по комнатному термометру, атмосферное давление – по барометру.

11.2.6.Вычислить среднюю длину свободного пробега и найти, используя эти данные, эффективный диаметр молекулы воздуха.

11.2.7.Радиус капилляра и его длину возьмите по указанию преподавателя.

11.2.8.Вычислить погрешности измерений <λ> и <d> по формулам

(11.11);(11.12)

Записать окончательный результат в виде

11.3.Контрольные вопросы

11.3.1.Какие явления называются явлениями переноса? Почему они так называются?

11.3.2.Дайте определение средней длины свободного пробега молекул и получите формулу (11.7) для определения <λ>.

11.3.3.Что понимают под эффективным диаметром молекул? Получите расчетную формулу для определения <λ>.

11.3.4.Исходя из уравнения состояния идеального газа, выведите формулу (11.9).

11.3.5.Какая связь между величинами, определяющими скорость молекул, среднюю длину свободного пробега их, и числом соударений в единицу времени.

11.3.6.Что называется коэффициентом вязкости, каков его физический смысл и каковы единицы измерения его в системе «СИ» и «СГС».

11.3.7.Докажите справедливость формул (11.11) и (11.12).

Литература

1. Лабораторный практикум по физике под редакцией В.А.Базакуцы, издательство Харьковского университета, 1969.

2. Описание к лабораторной работе «Определение длины свободного пробега и эффективного диаметра молекул воздуха». Издательство Московского станкостроительного института, 1967.

3. И.В. Савельев. «Курс общей физики», ч.1, 1977.

4. Яворский Б.М., Детлаф А.А. и др. «Курс физики», ч.1, 1973.

Оглавление

Стр.

Лабораторная работа № 1 – // – № 2 – // – № 3 – // – № 4 – // – № 5 – // – № 6 – // – № 7 – // – № 8 – // – № 9 – // – № 10 – // – № 11 Определение плотности твердого тела правильной формы. Определение ускорения силы тяжести по способу Бесселя. Определение ускорения силы тяжести наблюдением свободного падения тела. Изучение основного закона динамики вращательного движения. Определение момента инерции махового колеса динамическим методом. Определение длины звуковой волны и скорости звука по фазовым соотношениям. Изучение затухающих колебаний. Определение отношения удельной теплоемкости газа при постоянном давлении и удельной теплоемкости при постоянном объеме методом Клемана и Дезорма. Определение коэффициента вязкости жидкости. Изменение энтропии в процессах теплообмена. Определение средней длины свободного пробега и эффективного диаметра молекул воздуха.