Образец титульного листа
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ СЕРВИСА И ЭКОНОМИКИ
Институт сервиса автотранспорта, коммунальной и бытовой техники
Кафедра технической механики
КОНТРОЛЬНАЯ РАБОТА №___
ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
Номер зачетной книжки _____
Номер варианта_____
Работу выполнил студент _____группы А.Н.Шигин
Работу проверил доцент В.Н. Шабаев
Санкт-Петербург
Теоретическая механика
Статика
ПЛОСКАЯ ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ
Задача 1. Определить реакции RA и RB опор балки, размеры и нагрузки которой показаны на рис.1, а.


Рис. 1
Решение. 1. Составление расчетной схемы. Объект равновесия – балка АС. Активные силы: F = 3 кH, пара сил с M = 4 кH∙м распределенная нагрузка с интенсивностью q = 1 кН/м, которуюзаменяем одной сосредоточенной силой Rq = q∙ 1 = 1 ∙ 3 = 3 кH; приложенной к точке D на расстоянии 1,5 м от края консоли. Применяя принцип освобождаемости от связей изобразим в точках А и В реакции. На балку действует плоская произвольная система сил, в которой три неизвестных реакции 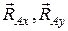 и
и  .
.
Ось х направим вдоль горизонтальной оси балки вправо, а ось у -вертикально вверх.
2. Условия равновесия:
 .
.
3. Составление уравнений равновесия:
 ,(1)
,(1)
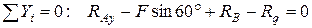 , (2)
, (2)
 . (3)
. (3)
4. Определение искомых величин, проверка правильности решения и анализ полученных результатов. Решая систему уравнений (1 – 3), определяем неизвестные реакции
из (1):
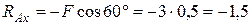 кН,
кН,
из (3):  ,
,
из (2):  кН.
кН.
Величина реакции RAх имеет отрицательный знак, значит направлена не так, как показано на рис. 18, а в противоположную сторону.
Для проверки правильности решения составим уравнение суммы моментов относительно точки Е.
 .
.
Подставив в это уравнение значения входящих в него величин, получим:
- 0,58 ∙ 1 – 4 + 5,02 ∙ 3 – 3 ∙ 3,5 = 0.
Уравнение удовлетворяется тождественно, что подтверждает правильность решения задачи.
Задача 2. На балку с защемленным концом (рис. 2, а) действует распределенная по линейному закону нагрузка интенсивностью q = 0,2 кН/м. Сила F = 10 кH действует под углом α = 45о к оси балки, кроме того, приложена пара сил с моментом М = 4 кH ∙м. Определить реакцию заделки.
а) б)


Рис.2
Решение.
1. Составление расчетной схемы (рис. 19, б). Объектом равновесия является балка АВ. К ней приложены активные силы  , пара сил с моментом
, пара сил с моментом  ираспределенная по линейному закону нагрузка. Равнодействующая
ираспределенная по линейному закону нагрузка. Равнодействующая  приложена в точке О,
приложена в точке О, 
Связью, наложенной на балку АВ,является жесткая заделка А. Применяя принцип освобождаемости от связей к балке АВ,заменим действие этой заделки на балку силами реакций 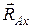 и
и 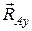 реактивным моментом
реактивным моментом  . Рассмотрим теперь равновесие балки АВ как свободного твердого тела, на которое действуют, кроме активных сил, еще и реакции связи.
. Рассмотрим теперь равновесие балки АВ как свободного твердого тела, на которое действуют, кроме активных сил, еще и реакции связи.
2. Усл овия равновесия:
 .
.
3. Составление уравнений равновесия. Для плоской произвольной
системы сил условиям равновесия соответствуют три уравнения:
 ; (а)
; (а)
 ; (б)
; (б)
 . (в)
. (в)
Для балки с жёсткой заделкой в качестве моментальной точки лучше брать заделку, что позволит исключить лишние неизвестные.
4. Определение искомых величин, проверка правильности решения и анализ полученных результатов.
Из уравнения (а) находим:
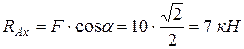 .
.
Из уравнения (б) получаем:
 .
. 
Наконец, из уравнения (в) находим:

Проверка. Составим уравнение моментов относительно точки В, подставим найденные реакции:
 .
.
Положительные значения реакций связей подтверждают правильность выбранных направлений этих сил.
Кинематика
Определение кинематических характеристик движения точки
Задача 1. Заданы уравнения движения точки М:

где х,у- координаты движущейся точки, см.
Установить вид траектории точки и для момента времени t=1 с найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение.
1. Преобразуем параметрические уравнения движения точки:

Получено уравнение окружности с центром в точке с координатами х=-2 см; у = 3 см и радиусом R = 2 см. После определения траектории имеется возможность изобразить её в декартовой системе координат (рис. 11.16) и установить положение точки М момент времени t = 1 с:

Если положение точки окажется вне траектории, следует прекратить дальнейшие расчёты и найти ошибку в предыдущих расчётах.
2. Найдём проекции скорости на оси координат:
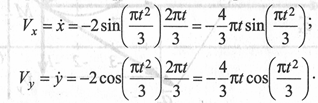
В момент времени t = 1 с Vx= -3,628 см/с; Vy = -2,094 см/с.
3. Определим модуль скорости:  В момент времени t= lc V=4,189 см/с. Покажем на рис. 11.16 в масштабе составляющие скорости
В момент времени t= lc V=4,189 см/с. Покажем на рис. 11.16 в масштабе составляющие скорости  ,
,  и вектор скорости
и вектор скорости  , который должен быть направлен по касательной к траектории. Если это не произошло, в расчётах допущена ошибка.
, который должен быть направлен по касательной к траектории. Если это не произошло, в расчётах допущена ошибка.
4. Найдём проекции ускорения на оси координат, учитывая, что  и
и  - сложные функции:
- сложные функции: 

В момент времени t = 1 с ax= -8,014 см/с2; ay =- 5,503 см/с2.
5. Определим модуль ускорения: 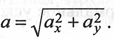 В момент времени t = 1с
В момент времени t = 1с
а = 9,721 см/с2.
Покажем на рис. 11.16 в масштабе составляющие ускорения ах, ау и вектор ускорения 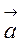 n, который должен быть направлен в сторону вогнутости траектории.
n, который должен быть направлен в сторону вогнутости траектории.

3.Вычислим касательное ускорение по формуле (11.28):

Положительный знак показывает, что движение точки М ускоренное, то есть направления векторов скорости и касательного ускорения совпадают.
4. Определим нормальное ускорение:

Покажем на рисунке векторы 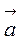 τ и
τ и 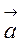 n,.
n,.
8.Определим радиус кривизны траектории:

Для окружности радиус кривизны траектории совпадает с радиусом окружности: ρ= R = 2 см. Результаты расчётов сведём в табл. 11.1.
Таблица 11.1

Динамика
ДИНАМИКА ТОЧКИ
Задача 1. В железнодорожных скальных выемках для защиты кюветов от попадания в них с откосов каменных осыпей устраивается «полка» DC. Учитывая возможность движения камня из наивысшей точки А откоса и полагая при этом его начальную скорость 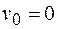 , определить наименьшую ширину полки b и скорость
, определить наименьшую ширину полки b и скорость  , с которой камень падает на нее. По участку АВ откоса, составляющему угол α с горизонтом и имеющему длину l, камень движется τ с. Коэффициент трения скольжения f камня на участке АВ считать постоянным, а сопротивлением воздуха пренебречь.
, с которой камень падает на нее. По участку АВ откоса, составляющему угол α с горизонтом и имеющему длину l, камень движется τ с. Коэффициент трения скольжения f камня на участке АВ считать постоянным, а сопротивлением воздуха пренебречь.
Дано:  . Определить b и
. Определить b и  (рис. 10.3).
(рис. 10.3).

Рис. 10.3
Решение. Задачу разделим на два этапа. Первый – движение камня на участке АВ, второй – движение камня от точки В до С.
Первый этап. 1. Составление расчетной схемы. Ось  проводим по направлению движения камня, ось
проводим по направлению движения камня, ось  - перпендикулярно к оси
- перпендикулярно к оси  . Камень принимаем за материальную точку и показываем ее в текущем положении, изображаем действующие на камень (точку) силы: вес
. Камень принимаем за материальную точку и показываем ее в текущем положении, изображаем действующие на камень (точку) силы: вес  , нормальную реакцию
, нормальную реакцию 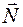 и силу трения скольжения
и силу трения скольжения  (рис. 10.4).
(рис. 10.4).
2.Выявление начальных условий.
При  .
.

Рис. 10.4
3.Составление дифференциальных уравнений движения точки. Так как точка (камень) движется прямолинейно, то при направлении оси х вдоль траектории получим одно дифференциальное уравнение движения
 ;
;
сила трения
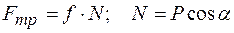 ,
,
тогда
 ;
;
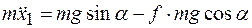 ;
;
 .
.
4.Интегрирование дифференциальных уравнений движения. Интегрируя дифференциальное уравнение дважды, получаем:
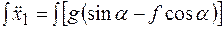 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
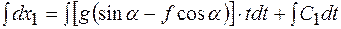 ;
;
 .
.
5.Определение постоянных интегрирования. Подставим начальные условия, т.е.  в уравнения:
в уравнения:
 ;
;
 ;
;

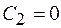 .
.
6.Нахождение неизвестных величин и исследование полученных результатов. После подстановки постоянных интегрирования С 1 и С 2 получаем уравнение скорости и уравнение движения:
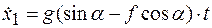 ;
;
 .
.
Для момента времени τ, когда камень покидает участок АВ,
 ,
,
т.е.
 ;
;
 .
.
Умножим первое уравнение на τ/ 2, после этого разделим его на второе. В результате получим:
 ;
;  ;
;
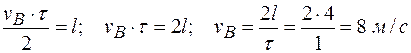 .
.
Второй этап. Движение камня от точки В до точки С.
1.Составление расчетной схемы. Координатные оси покажем так, как это удобно для решения задачи, в нашем случае ось х параллельна горизонтали и проходит через точку В, ось у направляем вниз через точку В. Камень принимаем за материальную точку, показываем ее в текущем положении, изображаем действующую на камень силу тяжести  (рис. 10.4).
(рис. 10.4).
2. Выявление начальных условий движения. При  :
: 
 .
.
3.Составление дифференциальных уравнений движения. Так как движение точки происходит в плоскости ху, то число уравнений движения равно двум:
 .
.
4.Интегрирование дифференциальных уравнений движения. Интегрируем дифференциальные уравнения дважды:
 (a)
(a)
 ; (б)
; (б)
 (в)
(в)
 . (г)
. (г)
5. Определение постоянных интегрирования. Подставляем начальные условия:  в уравнения (а – г):
в уравнения (а – г):

 ,
,
откуда
 .
.
6.Нахождение искомых величин и исследование полученных результатов. После подстановки постоянных интегрирования в уравнения (а –г) получаем следующие уравнения проекций скорости камня:

и уравнения его движения
 .
.
Уравнение траектории камня найдем, исключив параметр t из уравнений движения:
 ;
;
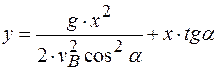 – уравнение параболы.
– уравнение параболы.
В момент падения  . Определим d из уравнения траектории:
. Определим d из уравнения траектории:
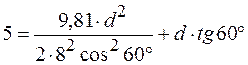 ;
;  ;
;
 .
.
Так как траекторией движения камня является ветвь параболы с положительными абсциссами ее точек, то d =2,11 м.
Минимальная ширина полки
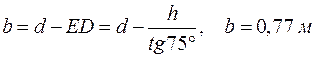 .
.
Используя уравнение движения камня  , найдем время Т движения камня от точки В до точки С
, найдем время Т движения камня от точки В до точки С
 .
.
Скорость камня при падении найдем через проекции скорости на оси координат:

по формуле
 .
.
Для момента падения t=T= 0,53 c
 .
.
Скорость камня при падении равна 12,8 м/с.






