К конструкциям, испытывающим косой изгиб, относятся прогоны и обрешетки в стропильных конструкциях: металлических или деревянных.
Пример 1. Проверить прочность деревянного прогона (сечение 100 х 220 мм) козырька над наружной входной дверью (рис. 2, а), если материал прогона — сосна первого сорта, длина козырька l= 3 м, угол наклона кровли α = 30°, шаг прогонов в горизонтальной проекции lгор = 1,5 м, удельная нагрузка от собственного веса покрытия с учетом веса прогона g1м2 = 1 кН/м2, удельная нагрузка от веса снега s1м2 = 2 кН/м2.
Решение. Полная нагрузка на 1 м2 горизонтальной проекции козырька
q 1м2 = g1м2 + s1м2 = 1+2 =3 кН/м2
Нагрузка на единицу длины прогона (один погонный метр) горизонтальной проекции (рис. 2, б):
q 1м п.гор = q 1м2 lгор = 3* 1,5 = 4,5 кН/м.
Для удобства последующих расчетов нагрузку q 1м п.гор обозначим q α 1м п. и разложим ее на две составляющие (рис. 2, б): перпендикулярную наклонной плоскости
q ┴1м п. = q α 1м п. cos α = 4,5 соs 30° = 4,5 • 0,866 = 3,9 кН/м;
параллельную наклонной плоскости
q ║1м п. = q α 1м п. sin α = 4,5 sin30° = 4,5 • 0,5 = 2,25 кН/м.
Нагрузка q α 1м п. приложена к верхней стороне сечения прогона и помимо изгиба вызывает его кручение. Если пренебречь кручением (как показывают опыты, это допустимо), нагрузку q α 1м п. можно перенести в центр тяжести сечения (рис. 2, в). Таким образом, мы имеем случай косого изгиба от нагрузки q α 1м п..
Нагрузки q ┴1м п. и q ║1м п вызывают изгибающие моменты в прогоне, который является простой балкой на двух опорах (рис. 2, г):
Мх = (q ┴1м п * l2)/ 8 = 4,39 кН• м = 439 кН• см;
Му = (q ║1м п ** l2)/ 8 = 2,53 кН • м = 253 кН • см.
Условие прочности при косом изгибе имеет вид
σтах (тiп) = Mx/Wx + My/Wy ≤ [σизг]
Моменты сопротивления сечения относительно осей х и y
Wx = bh2 /6= 10*22 2 / 6= 807 см3;
Wy = b2 h/6 = 22 * 10 2 /6 = 367 см3.
Сопротивление сосны первого сорта изгибу [σизг] = 14 МПа = = 1,4 кН/см2.
Подставляем числовые значения в условие прочности:
439кНсм / 807 см3 + 253кНсм / 367 см3 ≤ 14 кН/см2,
или 1,23 кН/см2 < 1,4 кНсм2.
Условие выполняется, т.е. прочность прогона обеспечена.
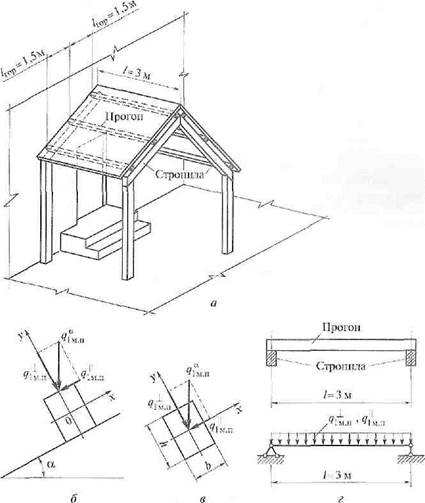
Рис. 2. К примеру 1:
а — изображение в аксонометрии козырька над входом; б — разложение наклонной нагрузки на составляющие, действующие вдоль наклонной плоскости и перпендикулярно ей; в — перенесение наклонной нагрузки в центр тяжести сечения; г — конструктивная и расчетная схемы прогона козырька
Пример 2. Подобрать размеры поперечного сечения (прямоугольник), для прямоугольника h=2b, а также определить положение нейтральной оси и перемещение конца балки рис.3. Построить для этой балки эпюру нормальных напряжений в опасном сечении.
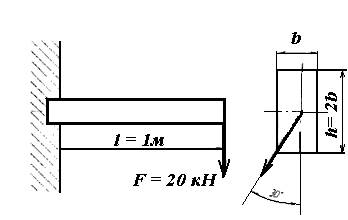
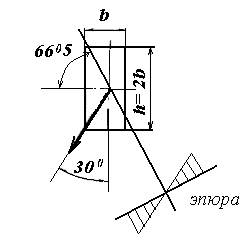
А б
Рисунок 3. К примеру 2.
Решение.
Раскладываем силу на F на составляющие, параллельные осям X и Y:
Fх = F • sinα = F * sin30° = 200 • 0.5 = 100 кН:
Fу = F• cos α= F • соs30° = 200 * 0.866 = 173.2 кН;
Опасным является опорное сечение, в котором действуют изгибающие моменты:
в горизонтальной плоскости Му = Fх *l = 100 • 1 = 100 кНм:
в вертикальной плоскости Мх = Fy *l =173.2 • 1 = 173,2 кНм.
Полный изгибающий момент в опасном сечении действует в той же плоскости,
в которой расположена сила F т.е. в плоскости наклоненной к оси у под углом α = 30°.
Используя формулу - tg β= tg α * Jx/Jy = (bh3 / (b3h) tg α = (h/b)2 tg α =22 *0.5774 = 2.3096
(так как по условию h/b = 2), откуда β = 66.58°. Положение нейтральной оси показано на рисунке.
Наибольшие по абсолютной величине нормальные напряжения возникают в
точках К1 К2 опасного сечения: в точке К1 напряжения растягивающие, а в
точке К2 -сжимающие.
используем формулу: σтах (тiп) = Mx/Wx + My/Wy = 1/Wx (Mx + WxMy/Wy)= 1/Wx (Mx +k My)
так как Wx/Wy = (bh2 /6) / (b2 h/6) = h/ b = 2.
Приравниваем наибольшее значение σ к допускаемому
напряжению [σ] = 130МПа, Е = 2 • 105 МПа:
σтах = 37,32/ W x =[σ]=130МПа,
откуда требуемый момент сопротивления сечения балки: Wx = 287076,92 мм3=287cм3.
При h/b = 2 Wx = bh2 /6 = 2b3/3
Следовательно.
b= 3√3Wx/2 =3√3* 287/2 = 7,55 см.
h = 2b = 2 *7,55 = 15,1см.
Эпюра нормальных напряжений для опасного поперечного сечения изображена
на рисунке 3.б.
Свободный конец балки под действием силы Fy = 173,2кН переместится по
вертикали на величину δy. а под действием силы Fх =100 кН переместится по горизонтали на величину δx. Величины δx и δy определяем по формуле полученной ранее:
δx = Fxl3 /3EJy; δy = Fyl3 /3EJx.
Jx = h3b/12 = 15.13 *7.55/12 = 2166,19 см4
Jу = hb3/12 = 15.1 *7.553/12 = 541,55 см4
δx = Fxl3 /3EJy =(100*103 *103)/ 2*3*105 * 541,55 * 104 = 0,00008 мм
δу = Fуl3 /3EJх = (172,3 *103* 103)/3*2*105 * 2166,19 * 104= 0,0000533 мм
Полное перемещение свободного конца
δ =√ δx2 + δу2=√0,000082+0,00005332=0,000096 мм
Направление перемещения: tg φ = δx/ δу
Задание для самостоятельной работы.
Подобрать размеры поперечного сечения прямоугольника с заданным соотношением сторон, а также определить положение нейтральной оси и перемещение конца балки. Построить для этой балки эпюру нормальных напряжений в опасном сечении. Принять [σизг] = 140МПа. Е = 2 • 105 МПа. Данные для своего варианта выбрать по таблице 1.
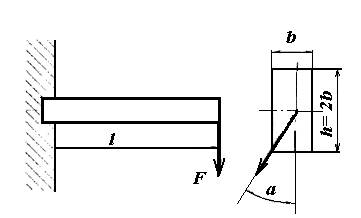
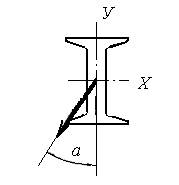
А б
Рисунок 4. Задание для самостоятельной работы.
| № варианта | Литер сече-ния | Сила F, кН | Длинна балки l, м | Угол α, град | № варианта | Литер сече-ния | Сила F, кН | Длинна балки l, м | Угол α, град |
| а | б | ||||||||
| б | 2,5 | а | 2,5 | ||||||
| а | б | ||||||||
| б | а | ||||||||
| а | 2,5 | б | 2,5 | ||||||
| б | а | ||||||||
| а | б | ||||||||
| б | 2,5 | а | 2,5 | ||||||
| а | б | ||||||||
| б | а | ||||||||
| а | 2,5 | б | 2,5 | ||||||
| б | а | ||||||||
| а | б | ||||||||
| б | 2,5 | а | 2,5 | ||||||
| а | б |
Этапы решения задачи
1. Перечертить схему.
2. Определить составляющие силы F на оси X и У.
3. Определить моменты в горизонтальной плоскости My, и в вертикальной плоскости Mx.
4. Определить положение нейтральной оси Х (по формуле tg β= tg α * Jx/Jy,).
5. Определить точки в которых возникают максимальные напряжения растяжения и сжатия и найти их значение.
6. Построить эпюру нормальных напряжений.
7. Определить размеры сечения.
8. Определить перемещение свободного конца δx и δy полное перемещение δ.
9. Определить момент инерции сечения.
10. Определить угол направления перемещения tg φ.
Контрольные вопросы
1. Охарактеризуйте напряженно-деформированное состояние балки при косом изгибе.
2. Сравните условие расчета балок на прочность при косом изгибе с аналогичным условием расчета при прямом изгибе. Чем отличаются подборы сечения балки при том и другом видах изгиба?
3. Как происходит косой изгиб балки?
4. Записать формулы момента инерции сечения круга, кольца. прямоугольника.
5. Записать формулы момента сопротивления сечения круга, кольца, прямоугольника.
6. Записать формулы для определения прогиба балки.






