Работа 13
ГРАДУИРОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ВОЛЬТМЕТРА С ПОМОЩЬЮ ЭЛЕКТРОМЕТРА ТОМСОНА
Цель работы. Градуирование шкалы электростатического вольтметра с помощью абсолютного электрометра Томсона, т.е. определение по основным (реперным) точкам соответствия между делениями шкалы прибора и измеряемой им разностью потенциалов, и придания делениям шкалы определенных значений в вольтах.
Введение
Электрическое поле, созданное неподвижными в данной системе отсчета электрическими зарядами, называется электростатическим полем. Силовой характеристикой такого поля является напряженность электрического поля 
, а энергетической – потенциал j.
Напряженностью электрического поля в какой-нибудь точке называется векторная величина, равная отношению силы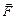 
, с которой это поле действует на неподвижный точечный пробный электрический заряд q, помещенный в данную точку поля, к величине этого заряда:
= 
. (1)
При этом предполагается, что внесение такого заряда во внешнее поле не искажает его [1, 2].
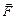Если заряд q положителен, направление силы совпадает с направлением ; при отрицательном знаке заряда и направлены в противоположные стороны.
Потенциалом j данной точки электростатического поля называется скалярная величина, равная отношению потенциальной энергии W П, которой обладал бы пробный точечный электрический заряд q, помещенный в данную точку поля, к величине этого заряда [2]:
j = 
. (2)
Силовая и энергетическая характеристика электростатического поля связаны соотношением [1]:
= - grad j = 
, (3)
где 
, 
, 
– единичные векторы, то есть орты соответствующих координатных осей.
Градиент потенциала j – это вектор, компонентами которого являются частные производные 
, 
, 
. Он численно равен быстроте изменения потенциала на единицу длины и направлен по нормали к эквипотенциальной поверхности, в сторону скорейшего возрастания потенциала. Из соотношения (3) следует, что напряженность электростатического поля направлена в сторону наиболее сильного убывания потенциала.
Работу, совершаемую силами электростатического поля по перемещению заряда q из точки 1 в точку 2, можно выразить через разность потенциалов j1 - j2 соответствующих точек пространства. Так как работа сил консервативного поля может быть представлена как убыль потенциальной энергии, учитывая соотношение (2), получаем:
A 12 = W П1 − W П2 = q (j1 - j2).
Откуда
j1 - j2 = 
(4)
Таким образом, разность потенциалов между двумя точками электростатического поля это физическая величина, числено равная работе, совершаемой силами этого поля по перемещению единичного пробного точечного заряда из одной точки в другую.
Если заряд q из точки с потенциалом φ удаляется на бесконечность (где по определению потенциал равен нулю), соотношение (4) принимает вид:
j = 
. (4')
Отсюда следует, что потенциал данной точки электростатического поля численно равен работе, которую совершают силы поля над единичным положительным точечным зарядом при удалении его из данной точки на бесконечность. Формулу (4') используют для установления единиц потенциала. Так, в СИ за единицу потенциала, называемую вольтом, принимается потенциал в такой точке, для перемещения в которую из бесконечности заряда, равного 1 кулону, нужно совершить работу в 1 джоуль[1]:
1В = 
Для измерения потенциалов используют предварительно отградуированный электростатический вольтметр. В настоящей работе градуирование осуществляется с помощью абсолютного электрометра Томсона.
Метод измерения и описание аппаратуры
В работе используется простейший электростатический вольтметр В (рис. 1а), устройство которого подобно устройству электроскопа. В отличие от последнего электростатический вольтметр снабжается шкалой, проградуированной в вольтах. На рис. 1а показан один из таких вольтметров. К медному стержню с шариком наверху крепится шкала, которую необходимо проградуировать в вольтах. В середине стержень имеет ступеньку, в которую вставляется горизонтальная ось алюминиевой стрелки. Стержень крепится к металлическому корпусу В вольтметра с помощью вмонтированной в него пробки из изоляционного материала.
Если, заземлив корпус, сообщить шарику заряд, зарядятся стержень и стрелка. Под действием сил отталкивания стрелка повернется на некоторый угол, указав на деление шкалы, соответствующее значению разности потенциалов между заземленным корпусом и стрелкой. Если такой вольтметр проградуировать, то им можно измерять разность потенциалов между любыми двумя проводниками, соединив один из них с корпусом вольтметра, а второй – с медным стержнем со стрелкой. Следует указать, что подобные вольтметры используются для измерения значений разности потенциалов от 100 В до 15000 В. При меньшей разности потенциалов стрелка отклоняется на очень небольшие углы, а при большей – трудно обеспечить надежную изоляцию.
Как отмечалось выше, для градуирования электростатического вольтметра в данной работе применяется абсолютный электрометр Томсона, представляющий собой весы Т (рис. 1а), одна из чашек которых заменена металлическим диском А, подвешенным на шарнире. Диск окружен металлической кольцевой пластиной С той же толщины, что и диск, называемой охранным кольцом. Такое кольцо обеспечивает однородность электростатического поля между пластинами А и П. Кольцо изолировано от нижней металлической пластины П брусочками из изоляционного материала (рис. 1б) и должно располагаться в одной плоскости с диском А. Нижняя пластина П устанавливается горизонтально с помощью трех винтов Д (рис. 1б), образуя с окруженным охранным кольцом диском А плоский воздушный конденсатор. В пределах диска электрическое поле такого конденсатора можно считать однородным, а электроемкость С удовлетворяющей соотношению:
С =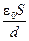 
. (5)
Здесь: S – площадь диска А, определяемая его диаметром D A; d – расстояние между обкладками конденсатора; ε0 – электрическая постоянная.
Такая форма конденсатора впервые была предложена В.Томсоном и применена в его электрометре, используемом для градуирования электростатического вольтметра.
При незаряженном конденсаторе диск А, заменивший одну из чашек весов, устанавливают на одном уровне с охранным кольцом. Если верхнюю подвижную обкладку конденсатора с охранным кольцом и корпус весов заземлить, а нижнюю обкладку П зарядить до некоторого потенциала φ зарядом q, то диск А будет притягиваться к нижней пластине. Поскольку в конденсаторе Томсона электростатическое поле однородно, сила притяжения диска будет равна
F = qE 1 = qE /2,(6)
где Е – напряженность электрического поля в конденсаторе; E 1− напряженность поля, создаваемого только пластиной П.
Напряженность электрического поля заряженной плоскости определяется выражением [1]:
E 1 = 
, (7)
Подставляя (7) в уравнение (6), получим:
F = 
. (8)
Заряд q можно выразить через электроемкость С и разность потенциалов между обкладками конденсатора Томсона j1 - j2 = U
q = C∙U = C∙ φ (9)
(в рассматриваемом случае разность потенциалов равна напряжению U, подаваемому на пластины конденсатора с высоковольтного блока питания (ВБП) (см. рис.1а). А поскольку верхняя обкладка заземлена (j2 = 0), то U = j1 = j). 
Учитывая, что для конденсатора Томсона электроемкость определяется соотношением (5), получаем:
F = 
U 2 = φ2 (10)
Как видно из соотношения (10), измерив с помощью весов Томсона силу F, можно определить потенциал φ. Это означает, что электростатические весы Томсона могут служить для абсолютных измерений потенциала и носят название абсолютного электростатического электрометра.
Чтобы с их помощью проградуировать электростатический вольтметр, его подсоединяют параллельно плоскому конденсатору. Из теории электростатического вольтметра известно, что его шкала, как правило, имеет квадратичный характер [3], т.е. угол отклонения стрелки α пропорционален квадрату разности потенциалов:
U 2 = βα, (11)
гдеβ– коэффициент, зависящий от параметров электростатического вольтметра.
Квадратичность его шкалы позволяет использовать такие вольтметры не только для измерения постоянного, но и переменного напряжения.
Из соотношений (10) и (11) получаем:
U 2 = 
= βα. (12)
Как указывалось выше, между диском А и охранным кольцом существует воздушный зазор, обычно не превышающий одного миллиметра. Это обстоятельство принимают во внимание при расчете площади S. Для этого к значению диаметра диска А (D A) добавляется средняя ширина ℓ зазора и в качестве расчетного диаметра берется D = D A + 2 
= D A + ℓ, а S = π D 2/4. Подставляя это значение S в (12), получим:
U 2 =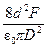 
= βα. (13)
Для того, чтобы проградуировать вольтметр, необходимо определить коэффициент β. Сделать это можно с помощью весов Томсона, определив из эксперимента силу F, при которой диск А начнет притягиваться к нижней пластине заряженного конденсатора. Для этого следует положить на вторую чашку весов Томсона разновес массой m и, подавая на вольтметр напряжение U от ВБП (рис.1а), определить отклонение стрелки вольтметра в делениях шкалы (α) в момент отхода диска от положения равновесия. В этот момент значение F=mg. Разным значениям массы m будут соответствовать различные углы отклонения α, т.е. различные значения напряжения U.
Рассчитав, используя уравнение (13), значения U 2, соответствующие применяемым в работе массам разновесов, строят график зависимости U 2 = f(α), из которого определяют значениеβ. Затем, полученное значение β используют для построения градуировочной кривой электростатического вольтметра U = f(α).
Необходимые для расчетов значения d, D А и ℓ указаны на каждой установке.
Приборы и принадлежности: электростатический вольтметр, абсолютный электрометр Томсона, высоковольтный блок питания, набор разновесов, соединительные провода.
Порядок выполнения работы
1. Собрать схему согласно рис. 1а. Во избежание больших утечек заряда соединительные провода должны быть достаточно короткими, без острых изгибов и заостренных концов. Провод высокого напряжения от ВБП подсоединить к стержню вольтметра, на котором находится подвижная стрелка, а сам стержень соединить с нижней пластиной П электрометра Томпсона. Земляной провод ВБП соединить с металлическим корпусом вольтметра и охранным кольцом С электрометра. Провода, идущие от разных полюсов, не должны близко подходить друг к другу, чтобы между ними не возникал разряд.
2. Уравновесить на весах собственный вес диска А гравием. Установить защитное кольцо так, чтобы ширина зазора между кольцом и диском была примерно одинаковой по всей окружности.
3. Установить при помощи винтов D (рис. 1б) пластину П горизонтально, а кольцо С и диск А – в одной горизонтальной плоскости. На диск и кольцо положить диэлектрическую палочку ДП, чтобы диск при колебаниях коромысла весов не поднимался выше уровня кольца (в качестве такой палочки можно использовать карандаш или шариковую ручку).
4. При первом измерении на чашу весов положить разновес массой 100мг. Для подачи напряжения на электростатический вольтметр нажать и удерживать красную кнопку «К» на верхней панели ВБП. Величину подаваемого напряжения изменяют регулятором напряжения «R» также расположенном на верхней панели ВБП. В момент, когда подвижная пластина конденсатора только начнет опускаться, замерить угол отклонения αстрелки вольтметра. При отпускании красной кнопки «К» высоковольтный провод автоматически заземляется и весь заряд с электростатического вольтметра стекает.
ВНИМАНИЕ! Перед каждым нажатием кнопки «К» регулятор «R» следует повернуть против часовой стрелки до упора. Это положение соответствует нулевому выходному напряжению ВБП.
5. Провести аналогичные измерения, изменяя массу разновеса от 100мг до 1г через каждые 100мг. Для большей точности каждый замер повторить пять раз. Результаты всех измерений записать в таблицу.
6. Для каждой массы разновеса рассчитать среднюю величину отклонения стрелки вольтметра:
<α> = (α1+α2+α3+α4+α5)/5, (14)
а также значения величин U 2 и U по формуле (13). Результаты записать в таблицу.
| № п/п | α, деления шкалы | <α> | m, г | U 2, кВ2 | U, кВ | ||||
| α 1 | α 2 | α 3 | α 4 | α 5 | |||||
| … |
Другие данные: DA=; d =; l =
7. Для каждой массы разновеса рассчитать погрешность определения α методом Стьюдента.
Δα = αст 
, (15)
где αст−коэффициент Стьюдента. Принять доверительную вероятность Р=0,9.
8. Построить график зависимости U 2 = f(α), из которого определить значение β. При построении графика нанести на экспериментальные точки значения погрешности Δα, полученные по формуле (15), в виде горизонтальных отрезков, проведенных через экспериментальные точки.
9. Используя полученное значение β, по уравнению (13) рассчитать и построить градуировочную кривую U = f(α) на миллиметровой бумаге.
Контрольные вопросы
1. Что означает выражение «градуирование вольтметра»?
2. Поясните принцип работы электростатического вольтметра. В чем его отличие от электроскопа?
3. Для какой цели в работе используется электрометр Томсона? Каково его устройство?
4. Почему электрометр Томсона называется абсолютным?
5. Дайте определение напряженности поля.
6. Дайте определение потенциала электростатического поля и разности потенциалов.
7. Как связаны между собой потенциал и напряженность электростатического поля?
8. Что представляет собой вектор градиент потенциала?
9. Дайте определение электроемкости проводника, конденсатора. Чему равна в системе СИ электроемкость плоского конденсатора?
10. Каков характер шкалы электростатического вольтметра и в чем его преимущества?
11. С какой целью в настоящей работе используется охранное кольцо?
12. С какой целью система электростатического вольтметра помещается в металлический кожух?
13. Можно ли кожух сделать из изоляционного материала?
14. Как определить коэффициент β? В каких единицах он измеряется?
15. Как построить градуировочную кривую?
Список литературы
1. Савельев И.В. Курс общей физики. Книга 2. Электричество и магнетизм. − М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2002.
2. Детлаф А.А., Яворский Б.М. Курс физики. − М.: «Высшая школа», 1989.
3. Физическая энциклопедия (ФЭ). ––М.– Научное издательство «Большая Российская энциклопедия». –– 1992.
Работа 14
ИЗУЧЕНИЕ ТОПОГРАФИИ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы. Опытное изучение топографии электростатического поля, т. е. экспериментальное нахождение пространственного распределения потенциала и напряжённости электростатического поля в зависимости от формы электродов и их расположения.
Введение
Электростатическим полем называют электрическое поле, созданное зарядами, неподвижными в данной системе отсчета.
Основными характеристиками электрического поля являются: вектор напряженности 
и потенциал φ.
Напряженность электрического поля − векторная физическая величина, измеряемая отношением силы 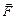, с которой электрическое поле действует на помещенный в данную точку неподвижный положительный пробный электрический заряд q 0к величине этого заряда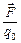[1]:
= 
. (1)
Напряженность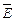 
является силовой характеристикойполя. Единицей напряженности в системе СИ является 1 В/м.
В каждой точке поля направление вектора напряженности совпадает с направлением вектора силы 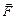, действующей на помещенный в данную точку поля пробный положительный заряд q 0 (рис.1).
Электрическое поле можно задать, указав для каждой точки величинуинаправление вектора .Совокупность этих векторов образует поле вектора напряженности электрического поля. Очень наглядно электрическое поле можно описать с помощью силовых линий.
| Рис.1 Направление и величина напряженности электрического поля создаваемого точечным положительным зарядом |
Силовая линия – это линия, касательная к которой в каждой точке совпадает с направлением вектора 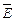(рис.2). Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной к линиям, было пропорционально численному значению вектора 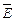. Силовым линиям приписывается направление: силовые линии начинаются на положительном заряде и заканчиваются на отрицательном (или уходят в бесконечность), либо приходят из бесконечности и заканчиваются на отрицательном заряде. Силовые линии не пересекаются между собой. Это следует из определения вектора 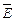как однозначной силовой характеристики каждой точки поля. В электростатическом поле силовые линии перпендикулярны поверхности проводника, т.к. заряды вдоль поверхности проводника не перемещаются. Таким образом по картине силовых линий можно судить о направлении и величине вектора 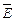в разных точках пространства.
Рис.2 Определение силовой линии |
Так как электрические силы являются центральными, работа силы, действующей на точечный заряд q 0 в электрическом поле при его перемещении, не зависит от формы траектории,а зависит лишь от начального и конечного положения заряда[1,2]. Такие поля называются потенциальными и работа по перемещению заряда q 0 из точки 1 в точку 2 может быть представлена как разность значений потенциальных энергий W п, которыми обладал заряд q 0 в точках 1 и 2 [2]:
A 12 = W П1 − W П2 (2)
Потенциальная энергия пропорциональна величине заряда q 0, перемещаемого в данном поле, а отношение потенциальной энергии к величине заряда не зависит от величины q 0 и поэтому характеризует само электрическое поле.
Потенциалом j данной точки электростатического поля называется скалярная величина, равная отношению потенциальной энергии W П, которой обладает положительный пробный точечный электрический заряд q 0, помещенный в данную точку поля, к величине этого заряда [2]:
j = 
. (3)
Разность потенциалов между точками 1 и 2 электрического поля определяется из выражения[2]:
j1 - j2 = 
= 
, (4)
т.е. разность потенциалов равна отношению работы по перемещению заряда q 0 из точки 1 в точку 2 к величине этого заряда.
Как и потенциальная энергия, потенциал электрического поля зависит от выбора нулевого уровня (точки, в которой потенциал считаетсяравным нулю). Условились считать потенциал точки, удаленной от заряда на бесконечность, равным нулю. Тогда φ2 = 0 и
j1 = 
. (5)
Следовательно, потенциал данной точки поля равен отношению работы, совершенной силами электрического поля по переносу пробного точечного заряда q 0 из данной точки поля в бесконечность (или в точку поля, для которой потенциал условно принято считать равным нулю), к величине переносимого заряда.
Потенциал – скалярнаявеличина, положительная или отрицательная – в зависимости от знака работы (пробный заряд q 0 условились всегда брать положительным). Из выражения (5) следует, что потенциалы всех точек вокруг положительного заряда положительные, вокруг отрицательного – отрицательные.
Потенциал является энергетической характеристикой электрического поля.
Единицей потенциала в СИ является 1В = 1 Дж/ Кл.
Для графического изображения электростатического поля можно вместо силовых линий воспользоваться эквипотенциальными поверхностями.
Эквипотенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал. Уравнение эквипотенциальной поверхности имеет вид
φ(x,y,z) = const.
Эквипотенциальные поверхности условились проводить таким образом, чтобы разность потенциалов для двух соседних поверхностей была всюду одна и та же. На плоском рисунке изображают эквипотенциали – линии пересечения эквипотенциальных поверхностей с плоскостью чертежа[4].
Напряженность электрического поля 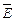и потенциал φ связаны между собой. Действительно, в потенциальном поле консервативных сил взаимосвязь силы 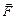и потенциальной энергии W п имеет вид[3]:
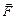= − grad W п. (6)
Разделив (6) на q 0, получаем:
= - grad j, (7)
где grad φ − вектор градиент потенциала φ. Знак минус указывает на то, что вектор направлен в сторону убывания потенциала. Градиент функции φ (х,у,z) в декартовой системе координат имеет вид:
grad j = 
,
где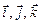 
− единичные векторы, т. е. орты соответствующих координатных осей; 
, 
, 
− частные производные φ.
Для произвольного направления работа сил электростатического поля на малом перемещении 
пробного заряда q
dA = q 
= qEdℓ cos(
^ ) = qE ℓ dℓ, (8)
где E ℓ − проекция вектора 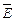на направление перемещения . С другой стороны
dA = −dW п = − qd φ. (9)
Из соотношений (8) и (9) следует, что
E ℓ = − 
, (10)
т.е. проекция вектора напряженности электростатического поля на произвольное направление равна скорости убывания потенциала в этом направлении.
При перемещении по эквипотенциальной поверхности на отрезок dℓ потенциал не изменяется (d φ = 0). Следовательно, согласно (10) касательная к поверхности составляющая вектора 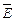равна нулю. Отсюда вытекает, что силовые линии вектора напряженности электростатического поля в каждой точке ортогональны к эквипотенциальным поверхностям.
Рис.3 Эквипотенциальные линии (пунктирные) и силовые линии (сплошные) поля 2-х точечных зарядов |
Из условия ортогональности силовых линий и эквипотенциальных поверхностей следует, что для графического описания поля достаточно каким-либо образом определить положение только эквипотенциальных поверхностей и затем, пользуясь этим условием, построить силовые линии. В качестве примера на рис.3 представлены эквипотенциали (пунктирные) и силовые линии (сплошные) для поля 2-х точечных зарядов. При одновременном использовании эквипотенциалей и силовых линий картина поля становится более наглядной.
Можно математически решить задачу о распределении в пространстве вектора напряженности 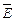и потенциала φ, найдя аналитические зависимости 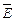и φ как функции координат x, y, z. Однако математический расчет электрического поля, создаваемого несколькими заряженными телами сложной конфигурации, иногда трудно осуществить. В таких случаях, моделируя реальные условия, находят распределение электрического поля опытным путем. При этом следует помнить, что графическое изображение в таких случаях часто является плоским, так как проводятся только те силовые линии, которые лежат в плоскости чертежа.
Из вышеизложенного следует, что если известно распределение эквипотенциальных поверхностей в данном поле, то можно получить его изображение с помощью силовых линий и наоборот. Следовательно, можно получить наглядную картину распределения электрического поля, т.е. топографию электрического поля. В данной работе требуется опытным путем выявить расположение эквипотенциалей нескольких видов полей и затем изобразить поля силовыми линиями.
