Исследование нестационарных процессов течения жидкости через гидродроссель
Цель работы и содержание работы
Исследовать режимы течения жидкости через гидродроссель, определение характеристик гидроаккумулятора.
Краткие теоретические сведения
Истечение жидкости из отверстия в тонкой стенке
Истечением называется частный случай течения жидкости, при котором потенциальная энергия жидкости, находящейся в резервуаре, превращается с большими или маленькими потерями в кинетическую энергию струи или капель.
Законы истечения жидкости имеют большое практическое значение, поскольку они применяются при решении многих технических задач, в том числе и в авиационной технике (подача топлива в камеры сгорания авиационных двигателей, течение через жиклеры в элементах автоматики жидкостно-газовых систем, в амортизационных стойках шасси и др.).
Задача об истечении обычно сводится к определению скорости истечения и расхода жидкости. Наиболее просто и точно она решается в случае, когда напор одинаков по всему поперечному сечению отверстия. Этому требованию удовлетворяет случай истечения из горизонтального отверстия в дне сосуда (рис.4.1).

Рис. 4.1. Истечение из донного отверстия
Рассмотрим течение жидкости, находящейся под давлением  из резервуара через относительно небольшое круглое отверстие с диаметром
из резервуара через относительно небольшое круглое отверстие с диаметром  в тонкой стенке дна, расположенное на глубине
в тонкой стенке дна, расположенное на глубине 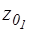 в воздушное пространство с давлением
в воздушное пространство с давлением 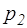 .
.
Будем полагать, что свободная поверхность и боковые стенки резервуара находятся далеко от отверстия и не влияют на приток жидкости к отверстию, поэтому частицы жидкости приближаются к нему из всего объема. Кроме того, примем, что уровень  поддерживается постоянным.
поддерживается постоянным.
Как показывает опыт, струя жидкости отрывается от стенки у кромки отверстия и несколько сжимается. Сжатие струи обусловлено необходимостью плавного перехода от различных направлений движения частиц жидкости в резервуаре к осевому направлению их движения в струе. На расстоянии, равном примерно диаметру отверстия, струя принимает цилиндрическую форму с диаметром 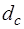 . Степень сжатия струи оценивается коэффициентом сжатия
. Степень сжатия струи оценивается коэффициентом сжатия
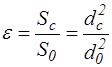 , (4.1)
, (4.1)
где  и
и 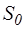 – площади поперечных сечений струи и отверстия соответственно.
– площади поперечных сечений струи и отверстия соответственно.
Запишем уравнение Бернулли для сечений 0 – 0 (свободная поверхность) и 2 – 2, где струя уже приняла цилиндрическую форму, и давление в ней стало равным 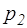 . Будем считать, что распределение скоростей по сечению струи равномерное, т.е.
. Будем считать, что распределение скоростей по сечению струи равномерное, т.е. 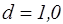
 , (4.2)
, (4.2)
где 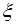 – коэффициент сопротивления отверстия.
– коэффициент сопротивления отверстия.
Введя расчетный напор
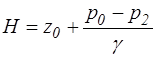
получим выражение для скорости истечения
 , (4.3)
, (4.3)
здесь 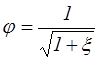 – коэффициент скорости.
– коэффициент скорости.
В случае идеальной жидкости коэффициент сопротивления отверстия 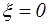 и скорость истечения равна теоретической
и скорость истечения равна теоретической
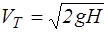 . (4.4)
. (4.4)
Таким образом, физический смысл коэффициента скорости в том, что он показывает отношение действительной скорости истечения к теоретической.
Расход жидкости при истечении
 . (4.5)
. (4.5)
Вводится коэффициент расхода 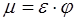 . Тогда
. Тогда
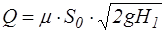 .
.
(4.5)
Безразмерные коэффициенты x, e, j, m зависят от формы отверстия и числа Re, подсчитанного по теоретической скорости (5.4), т.е.
 .
.
На рис.4.2 приведены зависимости указанных коэффициентов от  для круглого отверстия.
для круглого отверстия.

Из приведенных графиков видно, что с увеличением чисел  коэффициент скорости j возрастает. Это происходит потому, что из-за уменьшения роли сил вязкости уменьшается коэффициент сопротивления x. При
коэффициент скорости j возрастает. Это происходит потому, что из-за уменьшения роли сил вязкости уменьшается коэффициент сопротивления x. При  коэффициент
коэффициент  , а
, а  (случай идеальной жидкости). Коэффициент сжатия струи e при увеличении
(случай идеальной жидкости). Коэффициент сжатия струи e при увеличении  изменяется от 1,0 до 0,61. Изменение коэффициента расхода m является следствием изменения коэффициентов e и j. Наибольшее значение m достигается при
изменяется от 1,0 до 0,61. Изменение коэффициента расхода m является следствием изменения коэффициентов e и j. Наибольшее значение m достигается при 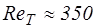 и равно
и равно  .
.
Следует отметить, что при больших числах  (маловязкие жидкости) коэффициенты e, j и m изменяются слабо, поэтому в расчетах обычно принимают следующие их значения:
(маловязкие жидкости) коэффициенты e, j и m изменяются слабо, поэтому в расчетах обычно принимают следующие их значения: 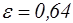 ,
, 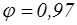 ,
, 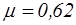 .
.
Если отверстие сделано не в дне, а в боковой стенке резервуара (вертикальной или наклонной), то приведенные формулы для скорости истечения и расхода, строго говоря, неприменимы. В этом случае напор не будет одинаковым во всем сечении отверстия и параметры истечения необходимо определять интегрированием по площади сечения параметров элементарных площадок отверстия. Однако можно показать, что если размеры отверстия малы по сравнению с размерами резервуара, то погрешности оказываются незначительными и для расчетов можно использовать формулы (4.1,…,4.6).
Истечение из отверстия при несовершенном сжатии струи
При рассмотренном истечении струя претерпевает наибольшее сжатие или, как принято называть, имеет место совершенное сжатие струи.
Если же боковые стенки резервуара расположены достаточно близко от отверстия, то они оказывают влияние на приток жидкости к отверстию и этот случай называется несовершенным сжатием струи.
В авиационных гидросистемах чаще всего используются цилиндрические резервуары, диаметры которых соизмеримы с диаметрами отверстий для истечения. При истечении из таких резервуаров через круглое отверстие, расположенное по оси резервуара (рис.4.3), существует эмпирическая зависимость для коэффициента сжатия
 , (4.7)
, (4.7)
 |
где
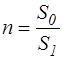 , а e определяется, как рассмотрено выше. При этом принимается
, а e определяется, как рассмотрено выше. При этом принимается 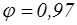 , а
, а 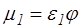 .
.
5.3. Несовершенное сжатие струи
Расход жидкости в этом случае равен
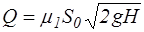 , (4.8)
, (4.8)
а расчетный напор
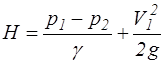 .
.
Встречаются случаи, когда отверстие какой-либо частью своего периметра непосредственно примыкает к стенке сосуда и сжатие на этой части периметра вообще не устраняется. Такое сжатие называется неполным. Коэффициент расхода при неполном сжатии определяется по формулам:
- для круглых отверстий
 ; (4.9)
; (4.9)
- для прямоугольных отверстий
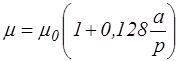 . (4.10)
. (4.10)
Здесь  – коэффициент расхода при совершенном сжатии; а – часть периметра отверстия, где устранено сжатие, т.е. где отверстие соприкасается со стенкой; p – полный периметр отверстия.
– коэффициент расхода при совершенном сжатии; а – часть периметра отверстия, где устранено сжатие, т.е. где отверстие соприкасается со стенкой; p – полный периметр отверстия.
Истечение при переменном напоре
Задача об истечении жидкости при переменном напоре обычно сводится к определению времени опорожнения или наполнения всего сосуда или некоторой его части в зависимости от начального наполнения, формы и размеров сосуда и отверстия.
В этом случае в отличие от рассмотренных задач истечения вследствие непрерывного изменения напора и, следовательно, непрерывного изменения скоростей и давлений всегда имеет место неустановившееся движение жидкости, что делает неприемлемым обычное уравнение Бернулли. Поэтому при решении таких задач полное время истечения разделяют на бесконечно малые промежутки, в течение каждого из которых напор считают постоянным, а движение жидкости установившемся. Это позволяет использовать для решения полученные выше зависимости и приводит к достаточно точным результатам.
Рассмотрим простейший пример истечения жидкости в атмосферу через данное отверстие площадью 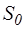 из открытого цилиндрического сосуда одинакового по всей высоте поперечного сечения S (рис.4.4).
из открытого цилиндрического сосуда одинакового по всей высоте поперечного сечения S (рис.4.4).
 |
Рис. 4.4. К определению времени опорожнения сосуда
Элементарный объем жидкости dQ, прошедшей через отверстие за бесконечно малый промежуток времени dt, будет составлять
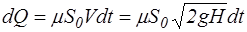 ,
,
где H – некоторое положение уровня жидкости в сосуде, который приближенно можно полагать постоянным; m – коэффициент расхода, зависящий от напора, формы и размеров отверстия.
Однако, в действительности за время dt уровень жидкости в сосуде опустится на dH и объем жидкости в нем изменится на величину  (знак «–» показывает, что с течением времени H уменьшается, следовательно, dH будет отрицательным).
(знак «–» показывает, что с течением времени H уменьшается, следовательно, dH будет отрицательным).
Вследствие неразрывности течения
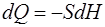
или
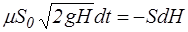 ,
,
откуда
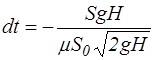 . (4.11)
. (4.11)
Полное время опорожнения сосуда определяется в результате интегрирования выражения (4.11)
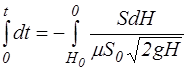 .
.
Меняя пределы интегрирования в правой части уравнения, принимая  и вынося постоянные за знак интеграла, будем иметь:
и вынося постоянные за знак интеграла, будем иметь:
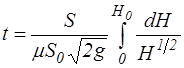 ,
,
что после интегрирования приведет к следующему окончательному выражению:
 . (4.12)
. (4.12)
Можно заметить, что при сохранении постоянного уровня в сосуде тот же объем жидкости пройдет через отверстие за время 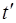 , вдвое меньше t. Действительно, поскольку полный объем жидкости в сосуде
, вдвое меньше t. Действительно, поскольку полный объем жидкости в сосуде  , а секундный расход при
, а секундный расход при 
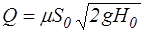 , то
, то
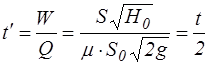 . (4.13)
. (4.13)
Формула (4.12) применима также к случаю истечения из отверстия в боковой стенке сосуда. В этом случае напор отсчитывается от геометрического центра тяжести отверстия.
Если требуется определить время, необходимое для понижения жидкости в сосуде на некоторую величину от 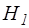 до
до 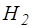 исходят из того же уравнения (4.11), интегрируя его в пределах от
исходят из того же уравнения (4.11), интегрируя его в пределах от 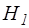 до
до 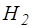 . При этом
. При этом
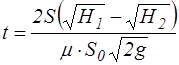 . (4.14)
. (4.14)
В общем случае, когда поперечное сечение сосуда изменяется по высоте, выведенные выше формулы неприменимы, так как в уравнении (4.11) площадь S – переменная величина. Тогда надо знать закон 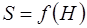 изменения площади поперечного сечения сосуда в зависимости от величины H.
изменения площади поперечного сечения сосуда в зависимости от величины H.
Уравнение (4.11) при этом приводится к виду
 . (4.15)
. (4.15)
Для сосудов геометрически правильной формы (шар, горизонтальный цилиндр) интегрирование уравнения (4.15) выполняется без особых затруднений. Если сосуд имеет неправильную форму, интегрирование производится численными или графическими методами.
Истечение под уровень
На практике иногда имеет место истечение жидкости не только в газообразную среду, как рассматривалось выше, но и в жидкость, уровень которой расположен выше отверстия (при этом оно может быть как в дне, так и в боковой стенке сосуда). Такой случай носит название истечение жидкости под уровень или в затопленное пространство (рис.4.5).
В этом случае расход определяется по формуле (4.6), как и при истечении в атмосферу, но напор принимается равным
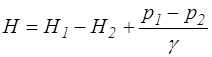 . (4.16)
. (4.16)
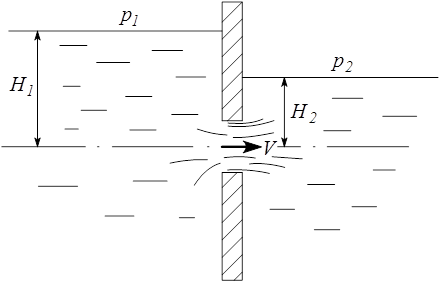
Рис. 4.5. Истечение под уровень
Если истечение в затопленное пространство происходит при переменном уровне, то время, необходимое для полного выравнивания уровней, может быть определено методами, аналогичными рассмотренным выше. При не изменяющихся по высоте поперечных сечениях сосудов это время
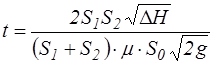 , (4.17)
, (4.17)
где  и
и 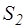 – площади поперечных сечений сосудов,
– площади поперечных сечений сосудов, 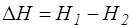 – разность уровней жидкости в них в начальный момент времени.
– разность уровней жидкости в них в начальный момент времени.
Время, необходимое для изменения разности уровней от 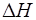 до
до  , определяется по уравнению
, определяется по уравнению
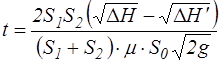 , (4.18)
, (4.18)
Истечение через насадки
Если стенка, через отверстие в которой происходит истечение, имеет значительную толщину по сравнению с размерами отверстия, то характер истечения существенным образом меняется, поскольку стенка влияет на струю. Такое же явление наблюдается, если к отверстию в тонкой стенке присоединить короткую трубку того же диаметра, что и отверстие. Такие трубки называются насадками, они имеют обычную длину не менее 2,5…3 диаметров отверстия.
Наиболее распространенными типами насадков являются:
- цилиндрические – внешний (рис.4.6,а) и внутренний (рис.4.6,б);
- конические – сходящийся (рис 4.6,в) и расходящийся (рис.4.6,г);
-
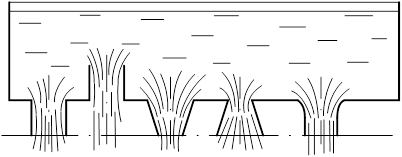 |
коноидальные, имеющие форму сжатой струи (рис.4.6,д).
А б в г д
Рис.4.6. Формы насадков
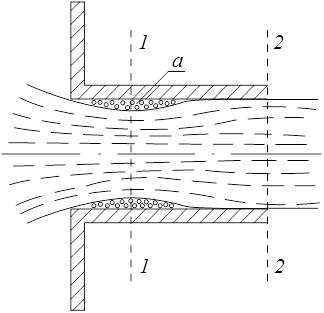
Рис. 4.7. Внешний цилиндрический НАСА
Рассмотрим истечение жидкости через внешний цилиндрический насадок (рис.4.7), представляющий собой короткую трубку длиной, равной нескольких диаметров  без закругления входной кромки.
без закругления входной кромки.
При истечении через такой насадок в газовую среду могут наблюдаться два режима течения.
При первом режиме струя при входе в насадок несколько сжимается 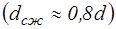 , затем постепенно расширяется и заполняет все поперечное сечение насадка. Сжатие струи происходит только внутри насадка (внутреннее сжатие), выходное же сечение насадка работает полностью, поэтому коэффициент сжатия, отнесенный к выходному сечению,
, затем постепенно расширяется и заполняет все поперечное сечение насадка. Сжатие струи происходит только внутри насадка (внутреннее сжатие), выходное же сечение насадка работает полностью, поэтому коэффициент сжатия, отнесенный к выходному сечению,  .
.
Экспериментально установлено, что величина коэффициента расхода m в этом случае зависит от отношения 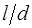 и числа Re, однако для практически значимых случаев можно принимать значение
и числа Re, однако для практически значимых случаев можно принимать значение 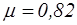 . А так как
. А так как  , то
, то 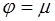 . Таким образом, если сравнивать истечение через внешний цилиндрический насадок с истечением из отверстия в тонкой стенке, то оказывается, что при истечении через насадок расход жидкости больше, а скорость истечения меньше. Объясняется это тем, что в месте сжатия струи внутри насадка образуется кольцевая вихревая полость “ a ” (см. рис.4.7). Наличие вихревой области в сочетании с явлениями сжатия и последующего расширения струи является причиной увеличения потерь напора и, следовательно, уменьшения скорости истечения.
. Таким образом, если сравнивать истечение через внешний цилиндрический насадок с истечением из отверстия в тонкой стенке, то оказывается, что при истечении через насадок расход жидкости больше, а скорость истечения меньше. Объясняется это тем, что в месте сжатия струи внутри насадка образуется кольцевая вихревая полость “ a ” (см. рис.4.7). Наличие вихревой области в сочетании с явлениями сжатия и последующего расширения струи является причиной увеличения потерь напора и, следовательно, уменьшения скорости истечения.
Следует заметить, что в узком сечении струи (сечение 1-1) скорость течения больше чем в сечении 2-2 (в соответствии с уравнением неразрывности), а давление меньше. С увеличением расчетного напора давление 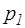 уменьшается и при некотором напоре, называемом критическим (
уменьшается и при некотором напоре, называемом критическим (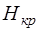 ), становится равным давлению насыщенных паров жидкости
), становится равным давлению насыщенных паров жидкости  , т.е. возникают условия для кавитации. При
, т.е. возникают условия для кавитации. При 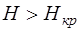 первый режим становится невозможным, струя внезапно отрывается от стенок насадка и наступает второй режим, ничем не отличающийся от истечения через отверстие. Коэффициент расхода при этом уменьшается до величины
первый режим становится невозможным, струя внезапно отрывается от стенок насадка и наступает второй режим, ничем не отличающийся от истечения через отверстие. Коэффициент расхода при этом уменьшается до величины  .
.
В случае внутреннего цилиндрического насадка по сравнению с внешним ухудшены условия для входа жидкости, вследствие чего увеличивается степень сжатия струи внутри насадка и увеличиваются потери напора на вихреобразования. При первом режиме истечения через такой насадок  . При втором режиме (
. При втором режиме (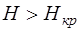 или
или 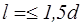 )
) 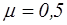 .
.
При истечении жидкости через затопленный цилиндрический насадок (под уровень) второй режим невозможен. В этом случае при 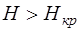 наступает кавитация, при которой расход перестает зависеть от давления
наступает кавитация, при которой расход перестает зависеть от давления 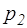 , т.е. получается эффект стабилизации расхода, используемый в кавитационных регуляторах расхода.
, т.е. получается эффект стабилизации расхода, используемый в кавитационных регуляторах расхода.
В коническом сходящемся насадке (рис.4.8) кроме явления внутреннего сжатия струи, которое здесь сказывается меньше, чем в цилиндрическом насадке, при выходе жидкости из насадка происходит второе (внешнее) сжатие, после чего она течет параллельными струйками.
Вследствие меньшего внутреннего сжатия потери напора в этом насадке меньше, чем в наружном цилиндрическом, скорость больше. Коэффициенты истечения зависят от угла конусности насадка q (см. рис.4.9). Из рисунка видно, что с увеличением q коэффициент расхода m сначала возрастает, достигая максимума (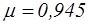 ) при
) при  , затем убывает. Конические сходящиеся насадки применяются в тех случаях, когда при данном напоре нужно получить большую скорость истечения.
, затем убывает. Конические сходящиеся насадки применяются в тех случаях, когда при данном напоре нужно получить большую скорость истечения.
 |
Рис. 48. Конический сходящийся насадок

Рис. 4.9. Зависимость коэффициентов истечения
от угла конусности насадка
Для конического расходящегося насадка внутреннее сжатие значительно больше, чем в коническом сходящемся и цилиндрическом насадках, поэтому в нем сильно возрастают потери и уменьшается коэффициент скорости j. Внешнего сжатия при выходе из такого насадка нет, поэтому  .
.
Коэффициенты j и m зависят от угла конусности q. При 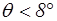 в среднем можно принимать
в среднем можно принимать  . При
. При 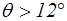 происходит отрыв струи от стенок, наступает второй режим истечения.
происходит отрыв струи от стенок, наступает второй режим истечения.
Конические расходящиеся насадки целесообразно применять в тех случаях, когда при заданном напоре нужно увеличить расход и в то же время уменьшить скорость истечения.
В коноидальном насадке, очерченном по форме струи, вытекающей из отверстия в тонкой стенке, коэффициенты скорости и расхода больше, чем во всех других насадках, рассмотренных выше, а именно 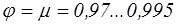 . Однако на практике коноидальные насадки используются редко из-за большой трудоемкости их изготовления, обычно вместо них используют конические сходящиеся насадки.
. Однако на практике коноидальные насадки используются редко из-за большой трудоемкости их изготовления, обычно вместо них используют конические сходящиеся насадки.
Экспериментальная часть
Последовательность выполнения лабораторной работы:
1. включить питание стенда;
2. включить электродвигатель (кнопка “Пуск”);
3. дать возможность установке поработать в течение 5 – 6 минут;
4. тумблер включения режима секундомера переключить в положение “АВТ.”;
5. включить тумблеры управления секундомером в положения “Вкл.” и “Пуск”;
6.провести опыты;
7.выключить электродвигатель, питание секундомера;
8.отключить питание стенда.
Экспериментальное исследование заключается в проведении 6-7 опытов по заполнению и опорожнению рабочей полости пружинного аккумулятора. Для этого необходимо воздействовать на тумблер управления гидрораспределителем Р2. При установке этого тумблера в положение “Вкл.” происходит заполнение полости аккумулятора, а при установке в положение “Выкл.” – опорожнение этой полости (которое происходит под действием пружины, взаимодействующей с поршнем). Исследование процессов заполнения рабочей полости аккумулятора провести при различных давлениях в напорной линии насоса (давления изменять в пределах 0,4…1,8 МПа путем перенастройки клапана КП, контроль давления – по манометру МН10).
Последовательность выполнения опыта:
1.обнулить показания секундомера;
2.переключить тумблер Р2 в положение «Вкл.»
3.после заполнения полости, записать значение времени в таблицу;
4.снять показания манометра Мн8 и занести их в таблицу;
5. обнулить показания секундомера;
6. переключить тумблер Р2 в положение «Выкл.»
7. после опорожнения полости, записать значение времени в таблицу.






