Лабораторная работа 2. Численные методы решения систем уравнений

 

Задание: решить систему уравнений (матрицы системы заданы в таблице) с точностью:

1. методом Крамера,

2. методом Гаусса с помощью расчетной таблицы,

3. методом простых итераций.

 

Вариант
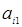
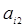
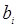
		10,21	–0,45	–0,2	1,91
	0,3	20,25	0,43	0,32
	0,6	–0,35	–10,25	1,83
		–30	0,5	0,5	–56,5
	0,5	-60	0,5	–100
	0,5	0,5	–30	–210
		20,45	–0,94	–0,15	–0,15
	–0,01	40,34	0,06	0,31
	–0,35	0,05	50,63	0,37
		10,63	0,05	0,15	0,34
	0,15	50,1	0,71	0,42
	0,03	0,34	70,1	0,32
		–30,20	1,6	–0,1	0,3
	–0,3	80,1	–1,50	0,4
	1,2	–0,2	30,3	–0,6
		10,3	1,2	–0,2	–0,6
	–0,1	–20,2	1,6	0,3
	0,05	0,34	50,1	0,32
		40,2	0,44	0,81	0,74
	0,58	–70,29	0,05	0,02
	0,05	0,34	80,1	0,32
		66,36	1,75	1,05	–1,40
	7,42	49,03	1,75	–49,49
	5,77	7,48	56,36	–27,67
		–91,11	1,02	–0,73	–1,25
	7,61	65,25	–2,32	2,33
	–4,64	1,13	–88,88	–3,75
		–99,11	1,02	–0,73	–1,25
	7,61	76,25	–2,32	2,33
	–4,64	1,13	–38,88	–3,75
		0,21	–0,45	–0,20	1,91
	0,30	0,25	0,43	0,32
	0,60	–0,35	–0,25	1,83
		–3	0,5	0,5	–56,5
	0,5	–6	0,5	–100
	0,5	0,5	–3	–210
		0,45	–0,94	–0,15	–0,15
	–0,01	0,34	0,06	0,31
	–0,35	0,05	0,63	0,37
		0,63	0,05	0,15	0,34
	0,15	0,10	0,71	0,42
	0,03	0,34	0,10	0,32
		–0,20	1,60	–0,10	0,30
	–0,30	0,10	–1,50	0,40
	1,20	–0,20	0,30	–0,60
		0,30	1,20	–0,20	–0,60
	–0,10	–0,20	1,60	0,30
	0,05	0,34	0,10	0,32
		0,20	0,44	0,81	0,74
	0,58	–0,29	0,05	0,02
	0,05	0,34	0,10	0,32
		6,36	11,75		–41,40
	7,42	19,03	11,75	–49,49
	5,77	7,48	6,36	–-27,67
		–9,11	1,02	–0,73	–1,25
	7,61	6,25	–2,32	2,33
	–4,64	1,13	–8,88	–3,75
		–9,11	1,02	–0,73	–1,25
	7,61	6,25	–2,32	2,33
	–4,64	1,13	–8,88	–3,75
		1,02	–0,73	–9,11	–1,25
	6,25	–2,32	7,62	2,33
	1,13	–8,88	4,64	–3,75
		0,06	0,92	0,03	–0,82
	0,99	0,01	0,07	0,66
	1,01	0,02	0,99	–0,98
		0,10	–0,07	–0,96	–2,04
	0,04	–0,99	–0,85	–3,73
	0,91	1,04	0,19	–1,67
		0,62	0,81	0,77	–8,18
	0,03	–1,11	–1,08	0,08
	0,97	0,02	–1,08	0,06
		0,63	–0,37	1,76	–9,29
	0,90	0,99	0,05	0,12
	0,13	–0,95	0,69	0,69
		0,98	0,88	–0,24	1,36
	0,16	–0,44	–0,88	–1,27
	9,74	-10,00	1,71	–5,31
		0,21	–0,94	–0,94	–0,25
	0,98	–0,19	0,93	0,23
	0,87	0,87	–0,14	0,33
		3,43	4,07	–106,00	46,8
	74,4	1,84	–1,85	–26,5
	3,34	94,3	1,02	92,3
		0,66	0,44	0,22	–0,58
	1,54	0,74	1,54	–0,32
	1,42	1,42	0,86	0,83
		0,78	–0,02	–0,12	0,56
	0,02	–0,86	0,04	0,77
	0,12	0,44	–0,72	1,01
		1,1	–0,2	0,1	1,6
	0,1	1,2	–0,2	–2,5
	0,2	–0,1	1,1	1,5
		0,63	0,05	0,15	0,34
	0,03	0,34	0,1	0,32
	0,15	0,1	0,71	0,42
			–5		–2
		1,2	–4,3	–1,1
	–6	3,3		–0,7
			–4	1,4	–0,6
			-3
	2,1	–1	–2	2,3
			–5		-3
		1,2	–4,3	–2,1
	–6	3,3		2,3

 

 

Лабораторная работа 3. Численные методы приближения функций.

1. По заданной таблице значений функции

 

 

Составить интерполяционный многочлен Лагранжа. Построить график и отметить на нем узловые точки. Вычислить приближенно значение функции, заданной таблично, в точке .

2. Дана функция 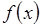. На заданном отрезке 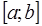построить интерполяционный многочлен Ньютона, используя 5 узлов интерполяции. Вычислить приближенно значение функции в точке . Оценить погрешность вычислений. Построить графики функции и интерполяционного многочлена, выделить узлы интерполяции.

3. Аппроксимировать функцию 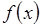(функция такая же, как и во втором задании) на указанном отрезке, используя 10 точек методом наименьших квадратов. Оцените погрешность вычисления значения функции в середине заданного отрезка с помощью аппроксимирующей функции.

 

 

Вариант	задание
		-1			-3			1,21
2,3	,	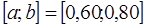0,61
								3,33
2,3	,	0,06
					-1	-4		0,54
2,3	,	0,91
						-2		10,11
2,3	,	0,16
		-3	-1			-1		0,26
2,3	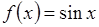,	0,51
					-3	-7		3,33
2,3	,	0,56
		-2	-1					1,55
2,3	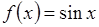,	0,11
						-3		4,56
2,3	,	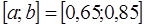0,66
		-4	-2					-1,55
2,3	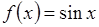,	0,21
		-1	1,5			-7		-0,55
2,3	,	0,36
		-1			-3			0,35
2,3	,	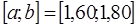1,61
								4,45
2,3	,
					-1	-4		1,57
2,3	,	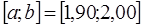1,91
						-2		8,69
2,3	,	1,16
		-3	-1			-1		2,27
2,3	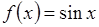,	1,51
					-3	-7		3,46
2,3	,	1,56
		-2	-1					-1,78
2,3	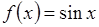,	1,11
						-3		3,23
2,3	,	1,66
		-4	-2					-2,94
2,3	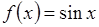,	1,21
		-1	1,5			-7		0,25
2,3	,	1,36
					-1	-6		6,21
2,3	,	2,61
		-9	-7	-4		-3		-5,41
2,3	,	2,66
						-1		3,65
2,3	,	2,91
		-8	-5			-2		-7,85
2,3	,	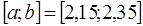2,16
		-7	-5	-4		-4		-6,81
2,3	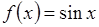,	2,51
					-2			6,54
2,3	,	2,56
						-2		9,62
2,3	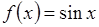,	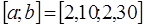2,11
		-4					-2	0,23
2,3	,	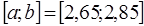2,66
		-3	-1			-1		0,05
2,3	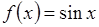,	2,21
							-4	4,69
2,3	,	2,36
								2,27
2,3	,	3,56
		-1						0,29
2,3	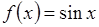,	4,11
								3,68
2,3	,	3,66
								2,78
2,3	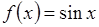,	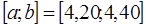4,21
					-7			3,56
2,3	,	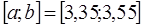3,36

Лабораторная работа 4. Численное интегрирование.

1. Найти приближенное значение интеграла по формулам левых и правых прямоугольников с точностью .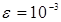

2. Найти приближенное значение интеграла по формуле средних прямоугольников с точностью .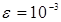

3. Найти приближенное значение интеграла по формуле трапеции с точностью .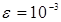

4. Найти приближенное значение интеграла по формуле Симпсона с точностью .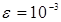

5. Сравнить полученные результаты

Интегралы для вычисления определяются исходя их номера варианта (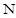 ‒ номер варианта студента).

 

Варианты	a)	b)
№1 - №10
№11 - №20
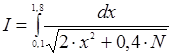
№21 - №30
№31 - №35