Лабораторная работа №5 Исследование функциональных узлов ЭВМ комбинационного типа
Цель работы: Практическое изучение логических функций и функциональных узлов их реализующих.
Краткие сведения из теории
Логической функцией f(x1, x2, …, xn) называется функция, которая принимает два значения 0 или 1 в зависимости от переменных хi, каждая из которых может также принимать только два значения 0 или 1.
В таблице наборы переменных расположены в определенном порядке, который совпадает с порядком возрастания наборов, рассматриваемых как двоичные числа. Этим упорядочиванием будем пользоваться и дальше.
Рассмотрим основные функции алгебры логики.
1. Логическое отрицание (инверсия) обозначается чертой над аргументом. Это функция одной переменной.
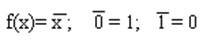
| (1.1) |
Схема, реализующая логическое отрицание, называется логическим элементом НЕ.
Графическое обозначение элемента.
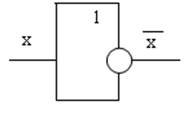
2. Логическое сложение (дизъюнкция). Это функция нескольких переменных. Функция обозначается следующим образом.
f(x1,x2) = x1 V x2 V x3…
Для двух переменных таблица истинности имеет вид.
Таблица 1.1 – Таблица истинности ИЛИ
| x1 | x2 | f(x1,x2) |
Условное графическое обозначение схемы ИЛИ.
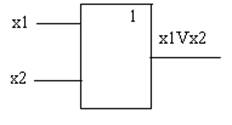
2. Логическое умножение (конъюнкция). Это функция нескольких переменных. Функция обозначается следующим образом.
| f(x1x2) = x1 /\ x2 /\ х3 … | (1.2) |
Функция определяется следующей таблицей истинности для двух переменных.
Таблица 1.2 – Таблица истинности И
| x1 | x2 | f(x1,x2) |
Условное графическое обозначение схемы И.
4. Функция Шеффера – реализует умножение с отрицанием. Определяется для двух переменных следующей таблицей истинности. Это функция нескольких переменных.
Таблица 1.3 – Таблица истинности
| x1 | x2 | f(x1,x2) |
Функция имеет вид.
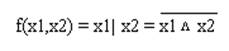
| (1.3) |
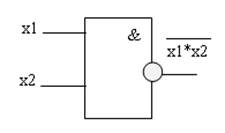
Условное графическое обозначение схемы И-НЕ.
5. Функция Пирса реализует логическое сложение с отрицанием. Определяется следующей таблицей истинности для двух переменных.
Таблица 1.4 – Таблица истинности
| x1 | x2 | f(x1,x2) |
Функция имеет вид.
| (1.4) |
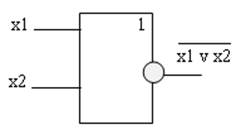
Условное графическое обозначение схемы ИЛИ-НЕ.
Функции дизъюнкции и конъюнкции могут быть не только функциями двух переменных. В общем случае произвольного числа аргументов.
6. Сложение по mod 2. Выполняет логическую операцию XOR. Это функция нескольких переменных и определяется следующей таблицей истинности для двух переменных.
Таблица 1.5 – Таблица истинности ИЛИ
| x1 | x2 | f(x1,x2) |
Функция имеет вид.
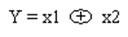
| (1.5) |
Условное графическое обозначение элемента исключающее ИЛИ.
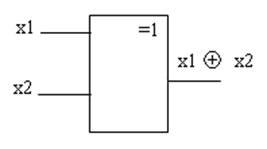
Всякая логическая функция “n” переменных может быть задана таблицей, в левой части которой перечислены все 2n наборов значений переменных, а в правой части – значения функции на этих наборах. Например, таблица для 3-х переменных представлена в таблице 1.6.
Таблица 1.6 – таблица истинности для 3-х переменных
| x1 | x2 | x3 | Y |
Наборы (строки) х на которых функция Y=1 называют единичным набором. Наборы х на которых Y=0, называют нулевым набором Y.
Составим логическую функцию из таблицы значений. Для этого возьмем конъюнкции аргументов в той строке, где функция равна единице. Причем, если аргумент равен нулю – он берется с инверсией. Если аргумент равен единице – он берется без инверсии. Полученные конъюнкции соединяем дизъюнкцией. Для нашего примера имеем три конъюнкции (три строки таблицы, где функция равна единице). Логическая функция имеет вид.
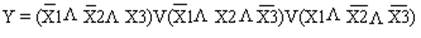
| (1.6) |
Инверсия обозначается чертой над аргументом. В первой конъюнкции аргумент Х1 b X2, взяты с инверсией, так как их значения во второй строке таблицы равны нулю. Во второй конъюнкции аргументы Х1 и Х3, взяты с инверсией, так как их значения в третьей строке таблицы равны нулю. В третьей конъюнкции аргумент Х2 и Х3 взяты с инверсией, так как их значения в пятой строке таблицы равны нулю. Полученные конъюнкции объединены операциями дизъюнкции.
Основные законы алгебры логики:
1. Переместительный закон. Коммутативность (лат. – менять, переменять);
X1 v X2 = X2 v X1 X1= 
X2=X2 X1
2. Сочетательный закон. Ассоциативность (лат. – соединять);
X1 v (X2 v X3) = (X1 v X2) v X3
X1 (X2 X3) = (X1 X2) X3
3. Распределительный закон. Дистрибутивность;
X1 (X2 v X3) = (X1 X2) v (X1 X3)
X1 v (X2 X3) = (X1 v X3) (X1 v X3)
4. Закон поглощения;
X1 v (X1 X2) = X1 X1 (X1 v X2) = X1
5. Закон склеивания;
X1X2 v X1X2 = X1 (X1 v X2)(X1 v X2) = X1
6. Правило де Моргана;
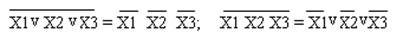
Выполнение логических операций производится в соответствии с приоритетами. В таблице представлены приоритеты выполнения логических операций.
Таблица 1.7 – Таблица приоритетов
| приоритет | операция |
| инверсия конъюнкция дизъюнкция сложение по mod 2 |
Операции одного приоритета выполняются слева направо. Для изменения порядка выполнения операций могут использоваться скобки.
Содержание работы:
1. Выбрать вариант в задании 1 из таблицы 1.8 и составить логическую функцию. Для первого варианта берутся значения Y1, для второго варианта берутся значения Y2 и т.д.;
2. Разработать принципиальную электрическую схему, реализующую логическую функцию и сохранить ее в формате gif или jpeg;
3. Исследовать работу комбинационной схемы;
5. По заданной принципиальной схеме составить таблицу истинности и логические функции;
Содержание отчета:
1. Постановка задачи;
2. Краткие сведения из теории;
3. Результаты выполнения заданий;
4. Ответы на контрольные вопросы.
Задание 1
Таблица 1.8 – Варианты заданий
| X1 | X2 | X3 | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y8 | Y9 | Y10 | Y11 | Y12 | Y13 | Y14 | Y15 | Y16 | Y17 | Y18 | Y19 | Y20 |
Y = (X1 X2 X3) v (X1 X2 X3)v (X1 X2 X3)v (X1 X2 X3)
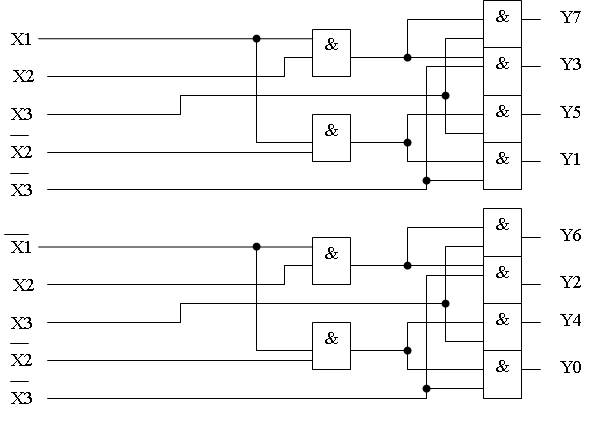
Задание 2
По заданной принципиальной схеме составить таблицу функционирования и логические функции.
Контрольные вопросы:
1. Дайте определение Булевой функции;
2. Назовите основные функции алгебры логики;
3. Составить таблицу истинности для функции Пирса;
4. Какие значения может принимать Булева функция;
5. Составить таблицу истинности для функции Шеффера;
6. Какой вид имеет функция Пирса;
7. Составьте таблицу истинности для логической операции XOR;
8. Найти значение функции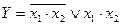 
при х1=0,х2=1;
9. Перечислите основные законы алгебры логики;
10. Какая логическая операция имеет высший приоритет;
11. Найти значение функции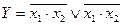 
Y=x1×x2 v x1×x2 при х1=1,х2=1;
12. Найти значение функции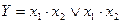 
при х1=1,х2=1.
Литература:
1. Сергеев Н.П., Вашкевич Н.П. Основы вычислительной техники. Учеб. Пособие для вузов. М.: высш. шк., 1988.-311с;
2. Новиков Ф. А. Дискретная математика для программистов: Учебник.СПб: Питер 2002. - 304 с;
3. Яворский В.В., Кан О.А.Дискретная математика для информационных систем. Учебник. Министерство образования и науки РК. КарГТУ, 2007.-197с.
