Степень с натуральным и рациональным показателем. Арифметический корень
С
тепенью с натуральным показателем n числа а называется произведение n сомножителей равных этому числу.
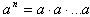- всего n сомножителей.
Например,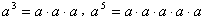 
.
Число а называют основанием, а число n называют показателем степени.
Степень с показателем 2 называют квадратом, а с показателем 3 – кубом.
Примеры:
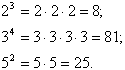
Корнем n-ой степени (n-натуральное число) из числа a (обозначение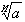 
) называют такое число x, степень которого равна a (
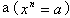). Эту операцию называют извлечением корня n-ой степени из a. Корень из положительного числа – всегда число положительное.
Корень второй степени не пишут, то есть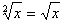 
.
Например,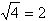 
, а не -2, хотя 
.
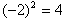Если число n – четное, то операция извлечения корня из отрицательного числа в поле действительных чисел не определена. Например, действительного числа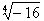 
не существует.
Степенью с рациональным показателем m/n числа x (степенью с дробным показателем) называют число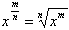 
, m и n – целые числа.
Например,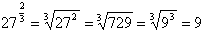 
Любое число, кроме 0, в нулевой степени равно 1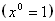 
. Операция 
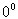не определена.
Еще одно важное соотношение
.
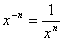Например: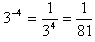 
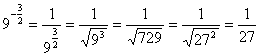
Степень с натуральным показателем {1, 2, 3,...}
Определем понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
- По определению:
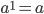. - Возвести число в квадрат — значит умножить его само на себя:
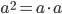
- Возвести число в куб — значит умножить его само на себя три раза:
.
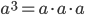Возвести число в натуральную степень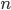 
— значит умножить число само на себя 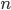раз:
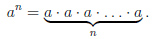
Степень с целым показателем {0, ±1, ±2,...}
Если показателем степени является целое положительное число:
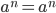, n > 0
Возведение в нулевую степень:
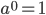, a ≠ 0
Если показателем степени является целое отрицательное число:
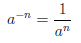, a ≠ 0
Прим: выражение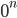 
не определено, в случае n ≤ 0. Если n > 0, то 
Пример 1.
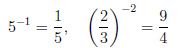
Степень с рациональным показателем
Если:
- a > 0;
- n — натуральное число;
- m — целое число;
Тогда:
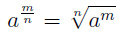
Пример 2.
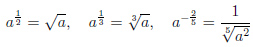
Свойства степеней
| Произведение степеней |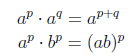 
|
| Деление степеней |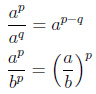 
|
| Возведение степени в степень |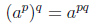 
|
Пример 3.
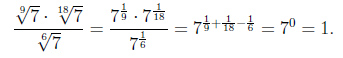
Корень
Арифметический квадратный корень
Уравнение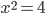 
имеет два решения: x=2 и x=-2. Это числа, квадрат которых равен 4.
Рассмотрим уравнение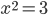 
. Нарисуем график функции 
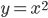и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.
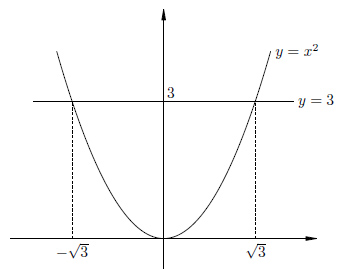
Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.
Арифметический квадратный корень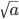 
— это неотрицательное число, квадрат которого равен 
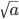, a ≥ 0. При a < 0 — выражение не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу .
Корень из квадрата
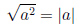
Например,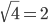 
. А решения уравнения 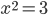соответственно 
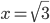и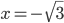 
Кубический корень
Кубический корень из числа — это число, куб которого равен . Кубический корень определен для всех . Его можно извлечь из любого числа: 
.
Корень n-ой степени
Корень 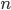-й степени из числа — это число, 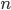-я степень которого равна .
Если 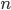— чётно.
- Тогда, если a < 0 корень n -ой степени из a не определен.
- Или если a ≥ 0, то неотрицательный корень уравнения
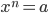называется арифметическим корнем n -ой степени из a и обозначается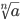 
Если 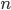— нечётно.
- Тогда уравнение 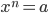имеет единственный корень при любом .
Пример 4.
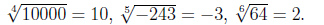
Таблица корней
| Корень третьей степени (3) |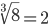 
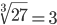
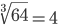
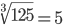
| Корень седьмой степени (7) |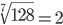 
|
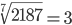
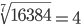
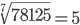
| Корень четвертой степени (4) |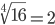 
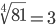
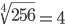
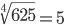
| Корень восьмой степени (8) |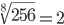 
|
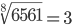
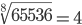
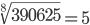
| Корень пятой степени (5) |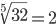 
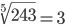
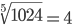
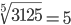
| Корень девятой степени (9) |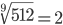 
|
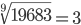
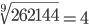
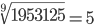
| Корень шестой степени (6) |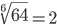 
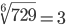
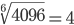
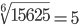
| Корень десятой степени (10) |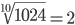 
|
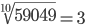
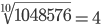
