Работа № 8
ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
ДВУХПОЛЮСНИКОВ
Цель работы: исследование амплитудно-частотных и фазовых характеристик входных сопротивлений 
- и 
- двухполюсников.
Подготовка к работе
В работе необходимо исследовать частотные характеристики реактивного LC-двухполюсника и RLC-двухполюсника, схемы которых представлены на рис. 8.1.
Рис. 8.1
При действии на цепь источника тока реакцией на входе является напряжение и свойства пассивного двухполюсника (ДП) в установившемся синусоидальном режиме определяются входным сопротивлением
.
График 
, построенный в функции частоты w, является в данном случае амплитудно-частотной характеристикой (АЧХ), график аргумента j(w) – фазочастотной характеристикой (ФЧХ), а графики 
и 
– соответственно вещественной и мнимой частотными характеристиками двухполюсника. Используют также амплитудно-фазовую характеристику (АФХ), представляющую собой геометрическое место значений 
, построенное в комплексной плоскости, например по графикам АЧХ и ФЧХ.
При резонансе в пассивном двухполюснике выполняются условия 
и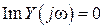 
, т. е. на резонансной частоте 
в установившемся синусоидальном режиме ток и напряжение двухполюсника совпадают по фазе: 
.
Для - двухполюсника входное сопротивление будет мнимой дробно-рациональной функцией w вида:
(8.1)
Нули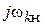 
и полюсы 
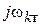сопротивления , определяемые соответственно из условия резонанса напряжений 
и условия резонанса токов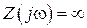 
, совпадают с резонансными частотами - двухполюсника. Они являются мнимыми числами и располагаются, чередуясь друг с другом, на оси 
плоскости комплексной частоты 
. В зависимости от структуры и элементов цепи в начале координат располагается либо нуль, как в (8.1), либо полюс. Обычно общее число резонансов напряжений и токов на единицу меньше количества реактивных элементов.
Используя указанные свойства реактивных двухполюсников, а также свойство dx / d w ³ 0, можно построить частотные характеристики jx (w) качественно. Например, для двухполюсника, изображенного на рис. 8.1, а, частотная характеристика jx (w), приведенная на рис. 8.2, а, может быть построена качественно для w > 0 исходя из следующих соображений: в цепи возможны лишь 3 резонансные частоты 
, 
и 
; предельные значения сопротивления x (0) = 0 и 
оцениваются путем анализа эквивалентной схемы замещения при w = 0 и w ® ¥.
Амплитудно-частотная характеристика 
этого идеализированного LC-двухполюсника определяется модулем функции, изображенной на рис. 8.2, а, поскольку 
. АЧХ двухполюсника с реальными катушками индуктивности и конденсаторами, полученная опытным путем, не принимает нулевых и бесконечно больших значений; она является непрерывной функцией частоты, но при высокой добротности контуров, исследуемых в работе (Q ³ 15…20), сохраняет большую крутизну в области резонансных значений частоты.
Для - двухполюсника в зависимости от соотношения значений параметров 
, 
, 
резонанс может и не наблюдаться. Следует также отметить, что в - двухполюсниках частоты, соответствующие максимальным
 |
и минимальным значениям 
, в общем случае не совпадают с резонансными.
Перед экспериментальным исследованием выполните следующее расчетное задание, необходимое для контроля опытных данных:
1. Вычислите резонансные частоты -двухполюсника, изображенного на рис. 8.1, а (
Гн, 
Гн, 
мкФ, 
мкФ), по формулам:
(8.2)
и постройте качественно график АЧХ двухполюсника.
2. Для -двухполюсника, изображенного на рис. 8.1, б, резонансная частота
(8.3)
Приняв Гн, мкФ выясните, при каком из значений резистора R, (используемых в работе 
кОм или 
кОм), резонанс невозможен, а при каком возможен; вычислите на основании (8.3) значение резонансной частоты и постройте качественно АЧХ - двухполюсника для обоих случаев.
Экспериментальные исследования
Для выполнения лабораторной работы откройте папку «Лаб. раб. ТОЭ» на рабочем столе компьютера и затем «Лаб. раб. №8». Для снятия частотных характеристик используется общая схема, изображенная на рис. 8.3, где ДП – двухполюсник, схема которого изображена на рис. 8.1, а. Выходной сигнал U вых соответствует напряжению на двухполюснике, а напряжение U вх пропорционально току, проходящему через него. Модуль входного комплексного сопротивления двухполюсника определяется
, т.к R1=1кОм (8.4)
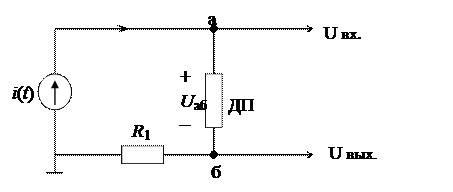
Рис.8.3
1. Исследование частотных характеристик - двухполюсника.
Исследования реактивного двухполюсника изображённого на рис.8.1а, проводятся в цепи, схема которой представлена на рис.8.4. К клеммам (а, б) подключён источник синусоидального тока с частотой f = 1 кГц и амплитудой I m = 0,05 мА. Для снятия частотных характеристик применяется Bode Plotter XBP1.
|
Для получения частотных характеристик необходимо, строго говоря, подать на входы Bode Plotter XBP1 напряжение двухполюсника U аа и пропорциональное току напряжение UR 1, снятое с сопротивления R 1. Хотя в схеме на рис. 8.3 вместо U аа к каналу Out подводится напряжение Uвх = U аа+ UR 1, вносимая ошибка невелика, так как в диапазоне исследуемых частот сопротивление R 1 много меньше сопротивления двухполюсника.
Активируйте цепь переключателем 
и двойным щелчком (2ЛК) мыши откройте лицевую панель Боде Плоттера и установите вначале для снятия АЧХ в режиме Magnitude по горизонтали (I =2kHz, F =10kHz, Lin), по вертикали (Lin, I =0, F =50). Передвигая измерительный курсор 
, определите резонансные частоты 
, 
, 
.
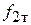Установите частоту F = 4kHz и снимите график вблизи ,зафиксировав частоты и значения АЧХ (Uвх/UR1) на пересечении кривой и сетки экрана. Затем включите F =10kHz и снимите остальную часть АЧХ вблизи 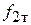. Результаты всех измерений занесите в табл.8.1. Включите кнопку [Phase] и снимите таким же образом ФЧХ j (f). Обязательно зафиксируйте минимальные при изменении знака и максимальные значения функции j (f) во всём диапазоне частот. Рассчитайте зависимость .
Постройте графики АЧХ и ФЧХ, сравните их с полученными качественно при подготовке к работе.
Таблица 8.1
| f, кГц | U ВХ/ UR1, | j,° | | Z |, кОм |
Вопросы:
1. В чем отличие частотных характеристик реальной цепи, составленной из катушек индуктивностей и конденсаторов, от характеристик идеальных реактивных двухполюсников?
2. Как проконтролировать полученные АЧХ и ФЧХ по эквивалентным схемам цепи f = 0, f = ¥, f = f 1т, f 2т?
2. Исследование частотных характеристик RLC- двухполюсника,
в котором резонанс возможен.
Откройте схему 2 цепи, изображенную на рис. 8.5. Используйте тот из резисторов, при котором на основании расчета по формуле (8.3) возможен резонанс.
|
Исследуйте АЧХ способом, аналогичным описанному в п. 1. Данные измерений в 8–9 точках диапазона частот, установив (Log, I =100Hz, F =2MHz) и по вертикали (Lin, I =0, F =15), занесите в таблицу подобную предидущей.
Затем снимите ФЧХ двухполюсника (I = -180, F =180). Вычислите 
.
Используя графики АЧХ и ФЧХ, изобразите АФХ. Для этого целесообразно определить по графику ФЧХ значения частот, соответствующих некоторым значениям угла j (например, j = ± 20°, ± 40° и т. д.). Затем для этих частот по АЧХ отсчитайте значения и нанесите на комплексную плоскость точки, соответствующие концам вектора 
. К полученным таким образом точкам АФХ добавьте точки, определяемые значениями при резонансной, нулевой и равной бесконечности частотах.
Вопрос 3. Можно ли по частотным характеристикам (АЧХ, ФЧХ, АФХ) определить резонансные частоты двухполюсника? По каким признакам?
3. Исследование частотных характеристик RLC-двухполюсника,
в котором резонанс невозможен.
Проведите в полном объеме исследования, аналогичные описанным в п. 2, используя второй резистор.
Вопросы:
4. В чем причина отсутствия резонанса в исследуемой - цепи и, какие из графиков (АЧХ, ФЧХ или АФХ) об этом свидетельствуют?
5. Как проконтролировать АЧХ, ФЧХ и АФХ цепи при f = 0 и f = ¥?
Требование к отчету
Отчет должен содержать цель работы, все пункты исследований и заключение. По каждому пункту в отчет необходимо включить название, принципиальные схемы исследуемых цепей, расчетные формулы и результаты расчета, таблицы опытных и расчетных данных, графики АЧХ, ФЧХ и АФХ, ответы на все поставленные вопросы.
