Тест состоит из двух частей: часть 1 направлена на проверку достижения базовой подготовки по курсу алгебры основной школы, часть 2 — на дифференцированную проверку повышенного уровня владения алгебраическим материалом.
Часть 1 содержит 16 заданий. К каждому заданию предложена одна из трех форм ответа: выбор ответа из четырех предложенных (надо обвести кружком букву, соответствующую верному ответу), краткий ответ (полученный ответ надо записать в отведенном для этого месте), соотнесение объектов из верхнего ряда с объектами из нижнего ряда (надо соединить соответствующие объекты любой линией).
Если при выполнении заданий этой части теста получено не более половины верных ответов, то это свидетельствует о неудовлетворительной подготовке к экзамену.
Часть 2 содержит 5 заданий, требующих развернутого ответа (с полной записью решения, выполненной на отдельных листах). При этом для каждого задания надо указать его номер и записать полностью его решение. Верное выполнение первых трех заданий подтверждает достаточно хорошую подготовку к экзамену.
Последние два задания отмечены звездочкой (*) как более трудные и предназначенные для учащихся, желающих попробовать свои силы при решении задач высокой сложности. Заметим для сильных учащихся: не пренебрегайте выполнением заданий части 1, т.к. отсутствие базовых умений нередко становится препятствием для получения отличной оценки.
ЧАСТЬ 1.
1. Упростите сумму  Ответ: __________________________________
Ответ: __________________________________
2. Упростите выражение  . А.
. А.  Б.
Б.  В. 4(1 + у) Г. 1 + у
В. 4(1 + у) Г. 1 + у
| А | Б | В | Г |
Ответ:
3. Для какой гиперболы нет соответствующего рисунка?
А. у =  Б. у =
Б. у =  В. у =
В. у = 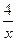 Г. у =
Г. у = 


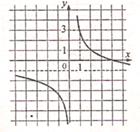
| А | Б | В | Г |
Ответ:
4. По графику функции у = f(х) определите, какое из утверждений верно:
А. При х = 0 функция принимает наименьшее значение.
Б. Функция возрастает на промежутке [0; + ∞).
В. Функция принимает положительные значения при х > 0.
Г. Область значений функции служит промежуток (-∞; - 2].

| А | Б | В | Г |
Ответ:
5. Для решения какой системы уравнений выполнен рисунок?

 А. х2 + у2 = 4
А. х2 + у2 = 4  Б. х2 + у = 4
Б. х2 + у = 4
х + у = - 2 х + у = - 2

 В. у = х2 + 4 Г. у = - х2 + 4
В. у = х2 + 4 Г. у = - х2 + 4
у = - х – 2 у = х – 2
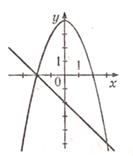
| А | Б | В | Г |
Ответ:
6. Какое из данных выражений не равно  ? А.
? А. 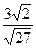 Б.
Б.  В.
В.  Г.
Г. 
| А | Б | В | Г |
Ответ:
7. Упростите выражение  Ответ: ____________________
Ответ: ____________________
8. Решите уравнение 5х2 + 20х = 0 Ответ: __________________________________
9. Сколько корней имеет уравнение –3х2 + 7х – 4 = 0
А. Один Б. Два В. Ни одного Г. Определить невозможно
| А | Б | В | Г |
Ответ:
10. Решите неравенство -3(х – 4) > х – 4(х – 1).
А. х < 0 Б. х > 0 В. Нет решений Г. х – любое рациональное число
| А | Б | В | Г |
Ответ:
11. На каком рисунке изображёно множество решений неравенства х2 – х – 12 ≤ 0?





 А. Б. В. Г.
А. Б. В. Г.
 |  |  |  |
- 3 4 - 3 4 - 3 4
| А | Б | В | Г |
Ответ:
12. На рисунке изображён график квадратичной функции на отрезке [-5; 2]. Найдите f(-8).
А. 1
Б. 5
В. 10
Г. Не существует
| А | Б | В | Г |
Ответ:

13. Найдите значение выражения (m-6)-2∙m-14 при m =  А. -16 Б.
А. -16 Б.  В.
В.  Г. 16
Г. 16
| А | Б | В | Г |
Ответ:
14. Запишите число 3,6 ∙ 10-5 в виде десятичной дроби.
А. 0,00036 Б. 0,000036 В. 0,0000036 Г. 0,00000036
| А | Б | В | Г |
Ответ:
15. Найдите значение выражения  при х = 0,4 и у = 0,3. Ответ: ________________
при х = 0,4 и у = 0,3. Ответ: ________________
16. Найдите корни уравнения  Ответ: ________________________
Ответ: ________________________
ЧАСТЬ 2
1) Упростите выражение  :
: 
2) Решите уравнение 2х4 – 19х2 + 9 = 0
3) Из пункта А в пункт В, расстояние между которыми 18 км, одновременно выезжают два велосипедиста. Скорость одного из них на 5 км/ч меньше скорости другого. Велосипедист, который первым прибыл в В, сразу же повернул обратно и встретил другого велосипедиста через 1 ч 20 мин после выезда из А. На каком расстоянии от пункта В произошла встреча?
4) Сравните:  и
и  .
.
5) Графиком квадратичной функции служит парабола с вершиной в точке D(3; 4), пересекающая ось ординат в точке К(0; -5). Задайте эту функцию формулой и постройте её график.






