ПРАКТИЧЕСКАЯ РАБОТА №3. ИЗМЕРЕНИЕ ИНФОРМАЦИИ
Содержательный подход.
Количество информации, заключенное в сообщении, определяется объемом знаний, который несет это сообщение получающему его человеку. Сообщение содержит информацию для человека, если заключенные в нем сведения являются для этого человека новыми и понятными и, следовательно, пополняют его знания.
При содержательном подходе возможна качественная оценка информации: полезная, безразличная, важная, вредная... Одну и ту же информацию разные люди могут оценить по разному.
Единица измерения количества информации называется бит. Сообщение, уменьшающее неопределенность знаний человека в два раза, несет для него 1 бит информации.
Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий (равновероятность обозначает, что ни одно событие не имеет преимуществ перед другими). Тогда количество информации, заключенное в этом сообщении, – х бит и число N связаны формулой:  .
.
Данная формула является показательным уравнением относительно неизвестной х. Из математики известно, что решение такого уравнения имеет вид:
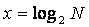
– логарифм от N по основанию 2. Если N равно целой степени двойки (2, 4, 8, 16 и т.д.), то такое уравнение можно решить «в уме». В противном случае количество информации становится нецелой величиной.
Пример 1. При бросании монеты сообщение о результате жребия (например, выпал орел) несет 1 бит информации, поскольку количество возможных вариантов результата равно 2 (орел или решка). Оба эти варианта равновероятны. Ответ может быть получен из решения уравнения: 2x = 2, откуда, очевидно, следует: х = 1 бит.
Вывод: в любом случае сообщение об одном событии из двух равновероятных несет 1 бит информации.
Пример 2. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)? Поскольку вытаскивание любого из 32 шаров равновероятно, то количество информации об одном выпавшем номере находится из уравнения: 2х = 32.
Но 32=25. Следовательно, х = 5 бит. Очевидно, ответ не зависит от того, какой именно выпал номер.
Пример 3. При игре в кости используется кубик с шестью гранями. Сколько бит информации получает игрок при каждом бросании кубика? Выпадение каждой грани кубика равновероятно. Поэтому количество информации от одного результата бросания находится из уравнения: 2х = 6.
Решение этого уравнения:  .
.
х = 2,585 бит.
Задачи
№ 1. «Вы выходите на следующей остановке?» – спросили человека в автобусе. «Нет», – ответил он. Сколько информации содержит ответ?
№ 2. Какой объем информации содержит сообщение, уменьшающее неопределенность знаний в 4 раза?
№ 3. Вы подошли к светофору, когда горел желтый свет. После этого загорелся зеленый. Какое количество информации вы при этом получили?
№ 4. Вы подошли к светофору, когда горел красный свет. После этого загорелся желтый свет. Сколько информации вы при этом получили?
№ 5. Группа школьников пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке номер 3. Сколько информации получили школьники из этого сообщения?
№ 6. В корзине лежат 8 шаров. Все шары разного цвета. Сколько информации несет сообщение о том, что из корзины достали красный шар?
№ 7. Была получена телеграмма: «Встречайте, вагон 7». Известно, что в составе поезда 16 вагонов. Какое количество информации было получено?
№ 8. В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал Пете?
№ 9. При угадывании целого числа в диапазоне от 1 до N было получено 7 бит информации. Чему равно N?
№ 10. При угадывании целого числа в некотором диапазоне было получено 6 бит информации. Сколько чисел содержит этот диапазон?
№ 11. Сообщение о том, что ваш друг живет на 10 этаже, несет 4 бита информации. Сколько этажей в доме?
№ 12. Какое количество информации несет сообщение: «Встреча назначена на сентябрь».
Алфавитный подход
Алфавитный подход к измерению информации позволяет определить количество информации, заключенной в тексте. Алфавитный подход является объективным, т.е. он не зависит от субъекта (человека), воспринимающего текст.
Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью (размером) алфавита. Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле:
 ,
,
где N – мощность алфавита. Следовательно, в 2-х символьном алфавите каждый символ «весит» 1 бит (  ); в 4-х символьном алфавите каждый символ несет 2 бита информации (
); в 4-х символьном алфавите каждый символ несет 2 бита информации (  ); в 8-ми символьном – 3 бита (
); в 8-ми символьном – 3 бита (  ) и т.д.
) и т.д.
Один символ из алфавита мощностью 256 (28) несет в тексте 8 бит информации. Такое количество информации называется байт. Алфавит из 256 символов используется для представления текстов в компьютере. 1 байт = 8 бит.
Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен: I = К х i,
где i – информационный вес одного символа в используемом алфавите.
Для измерения информации используются и более крупные единицы:
1 Кбайт (килобайт) = 210 байт = 1024 байта
1 Мбайт (мегабайт) = 210 Кбайт = 1024 Кбайта
1 Гбайт (гигабайт) = 210 Мбайт = 1024 Мбайта
Пример 4. Книга, набранная с помощью компьютера, содержит 150 страниц; на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге?
Решение. Мощность компьютерного алфавита равна 256. Один символ несет 1 байт информации. Значит, страница содержит 40 х 60 = 2400 байт информации. Объем всей информации в книге (в разных единицах):
2400 х 150 = 360 000 байт.
360000/1024 = 351,5625 Кбайт.
351,5625/1024 = 0,34332275 Мбайт.
Задачи
№ 1. Алфавит племени Мульти состоит из 8 букв. Какое количество информации несет одна буква этого алфавита?
№ 2. Сообщение, записанное буквами из 64-х символьного алфавита, содержит 20 символов. Какой объем информации оно несет?
№ 3. Племя Мульти имеет 32-х символьный алфавит. Племя Пульти использует 64-х символьный алфавит. Вожди племен обменялись письмами. Письмо племени Мульти содержало 80 символов, а письмо племени Пульти – 70 символов. Сравните объемы информации, содержащейся в письмах.
№ 4. Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?
№ 5. Объем сообщения, содержащего 2048 символов, составил 1/512 часть Мбайта. Каков размер алфавита, с помощью которого записано сообщение?
№ 6. Сколько символов содержит сообщение, записанное с помощью 16-ти символьного алфавита, если объем его составил 1/16 часть Мбайта?
№ 7. Сколько килобайтов составляет сообщение, содержащее 12288 битов?
№ 8. Сколько килобайтов составит сообщение из 384 символов 16-ти символьного алфавита?
№ 9. Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержат 5 страниц текста?
№ 10. Сообщение нанимает 3 страницы по 25 строк. В каждой строке записано по 60 символов. Сколько символов в использованном алфавите, если все сообщение содержит 1125 байтов?
№ 11. Для записи сообщения использовался 64-х символьный алфавит. Каждая страница содержит 30 строк. Все сообщение содержит 8775 байтов информации и занимает 6 страниц. Сколько символов в строке?
№ 12. Сообщение занимает 2 страницы и содержит 1/16 Кбайта информации. На каждой станице записано 256 символов. Какова мощность использованного алфавита?
Количество информации и вероятность
Рассмотрим несколько примеров.
Пример 1. В коробке имеется 50 шаров. Из них 40 белых и 10 черных. Очевидно, вероятность того, что при вытаскивании «не глядя» попадется белый шар больше, чем вероятность попадания черного.
Решение. Обозначим рч – вероятность попадания при вытаскивании черного шара, рб – вероятность попадания белого шара. Тогда:
рч = 10/50 = 0,2; р6 = 40/50 = 0,8.
Отсюда видно, что вероятность попадания белого шара в 4 раз больше, чем черного.
Пример 2. Сережа – лучший ученик в классе. Вероятность того, что за контрольную по математике Сережа получит «5» больше, чем вероятность получения двойки.
Решение. Представим себе, что мы изучили успеваемость Сережи за несколько лет учебы. За это время он получил по математике 100 оценок. Из них: 60 пятерок, 30 четверок, 8 троек и 2 двойки. Допуская, что такое распределение оценок может сохраниться и в дальнейшем, вычислим вероятность получения каждой из оценок.
р5 = 60/100 = 0,6; р4 = 30/100 = 0,3;
р3, = 8/100 = 0,08; р2 = 2/100 = 0,02.
Пример 3. В пруду живут 8000 карасей, 2000 щук и 40 000 пескарей. Самая большая вероятность для рыбака – поймать в этом пруду пескаря, на втором месте – карась, на третьем – щука.
Решение. Всего в пруду обитают 50000 рыб. Из предыдущих примеров можно догадаться, что вероятность попадания на удочку каждого из видов рыб равна его доле в общем количестве. Отсюда: рк = 8000/50000 = 0,16;
рщ = 2000/50000 = 0,04;
рп = 40000/50000 = 0,8.
Из рассмотренных примеров можно сделать вывод: если N – это общее число возможных исходов какого-то процесса (вытаскивание шара, получение оценки, ловля рыбы), и из них интересующее нас событие (вытаскивание белого шара, получение пятерки, попадание щуки) может произойти К раз, то вероятность этого события равна K/N.
Вероятность выражается в долях единицы. В частном случае, вероятность достоверного события равна 1 (из 50 белых шаров вытащен белый шар); вероятность невозможного события равна нулю (из 50 белых шаров вытащен черный шар).
Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
Например, сообщение о том, что Сережа получил двойку по математике, содержит больше информации для тех, кто его знает, чем сообщение о пятерке. Сообщение, что рыбак поймал в пруду щуку, более информативно, чем сообщение о том, что на удочку попался пескарь. Количественная зависимость между вероятностью события (р) и количеством информации в сообщении о нем (i) выражается формулой:
 .
.
Пример 4. В задаче о шарах определим количество информации в сообщении о попадании белого шара и черного шара:
iб = log 2 (l/0,8) = log 2 (l,25) = 0,321928;
iч = log 2 (l/0,2) = log 2 5 = 2,321928.
Вероятностный метод применим и для алфавитного подхода к измерению информации, заключенной в тексте. Известно, что разные символы (буквы алфавита, знаки препинания и др.) встречаются в тексте с разной частотой и, следовательно, имеют разную вероятность. Значит, измерять информационный вес каждого символа в тексте так, как это делалось раньше (в предположении равновероятности), нельзя.
Пример 5. В алфавите племени МУМУ всего 4 буквы (А, У, М, К), один знак препинания (точка) и для разделения слов используется пробел. Подсчитали, что в популярном романе «Мумука» содержится всего 10000 знаков, из них: букв А – 4000, букв У – 1000, букв М – 2000, букв К – 1500, точек – 500, пробелов – 1000. Какой объем информации содержит книга?
Решение. Поскольку объем книги достаточно большой, то можно допустить, что вычисленная по ней частота встречаемости в тексте каждого из символов алфавита характерна для любого текста языке МУМУ. Подсчитаем частоту встречаемости каждого символа во всем тексте книги (т.е. вероятность) и информационные веса символов:
буква А: 4000/10000 = 0,4; iA=log 2 (1/0,4) = 1,321928;
буква У: 1000/10000 = 0,1; iУ=log 2 (1/0,1) = 3,1928;
буква М: 2000/10000 = 0,2; iМ=log 2 (1/0,2) = 2,321928;
буква К: 1500/10000 = 0,15; iК=log 2 (1/0,15) = 2,736966;
точка: 500/10000 = 0,05; iточка=log 2 (1/0,05) = 4,321928;
пробел: 1000/10000 = 0,1; iпробел=log 2 (1/0,1) = 3,321928.
Общий объем информации в книге вычислим как суму произведений информационного веса каждого символа на число повторений этого символа в книге:
I = iА х nА + iУ х nУ + iМ х nМ + iК х nК + iточка х nточка + iпробел х nпробел =
=1,321928х4000+3,1928х1000+2,321928х2000+2,736966х1500+4,321928х500+3,321928х100=22841,84 бита.
Задачи
№ 1. В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар?
№ 2. В корзине лежат 32 клубка шерсти. Среди них – 4 красных. Сколько информации несет сообщение о том, что достали клубок красной шерсти?
№ 3. В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в корзине?
№ 4. В ящике лежат перчатки (белые и черные). Среди них – 2 пари черных. Сообщение о том, что из ящика достали пару черных перчаток, несет 4 бита информации. Сколько всего пар перчаток было в ящике?
№ 5. В классе.30 человек. За контрольную работу по математике получено 6 пятерок, 15 четверок, 8 троек и 1 двойка. Какое количество информации в сообщении о том, что Иванов получил четверку?
№ 6. Известно, что в ящике лежат 20 шаров. Из них 10 – черных, 5 – белых, 4 – желтых и 1 – красный. Какое количество информации несут сообщения о том, что из ящика случайным образом достали черный шар, белый шар, желтый шар, красный шар?
№ 7. За четверть ученик получил 100 оценок. Сообщение о том, что он получил четверку, несет 2 бита информации. Сколько четверок ученик получил за четверть?
№ 8. В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров?
№ 9. Частотный словарь русского языка – словарь вероятностей (частот) появления букв в произвольном тексте – приведен ниже. Определите, какое количество информации несет каждая буква этого словаря.
| Символ | Частота | Символ | Частота | Символ | Частота | Символ | Частота |
| о | 0.090 | в | 0.035 | я | 0.018 | ж | 0.007 |
| е, ё | 0.072 | к | 0.028 | ы, з | 0.016 | ю, ш | 0.006 |
| а, и | 0.062 | м | 0.026 | ь, ъ, б | 0.014 | ц, щ, э | 0.003 |
| т,н | 0.053 | д | 0.025 | ч | 0.013 | ф | 0.002 |
| с | 0.045 | п | 0.023 | й | 0.012 | ||
| р | 0.040 | у | 0.021 | х | 0.009 |
№ 10. Используя результат решения предыдущей задачи, определите количество информации в слове «ИНФОРМАТИКА».
№ 11. Используя решение задачи №10, определите количество информации в фразе «ПОВТОРЕНИЕ – МАТЬ УЧЕНИЯ».
4. Продолжите последовательность:
1) 1, 4, 8, 16,
2) 1, -2, 3, -4
3) 1, 1, 2, 3, 5, 8, 13,
4) о, д, т, ч, п, ш, с, в, д, д,
5. Черный ящик. Задумано правило обработки информации – «черный ящик». Это устройство преобразует входную последовательность символов в выходную последовательность. По заданным примерам установите правило работы черного ящика.
1) А Þ Б, ЭВМ Þ ЮГН, язык Þ аиъл
2) 12 Þ 0, 7Sg Þ 0, DFV Þ 0, РФ Þ 0
3) 1 Þ 1, 12 Þ 3, 111 Þ 3
4) Б Þ 1, МАМА Þ 4, ПК Þ 2
Ответы:
Содержательный подход
№1 1 бит; №2 2 бита; №3 1 бит; №4 0 бит; №5 2 бита; №6 3 бита; №7 4 бита; №8 7 битов; №9 128; №10 64; №11 16; №12 3,58496 бита.
Алфавитный подход
№1 3 бита; №2 120 бит; №3 400 и 420 бит; №4 16 символов; №5 256 символов; №6 131072 символа; №7 1,5 Кбайта; №8 0,1875 Кбайта; №9 10500 байт; №10 4 символа; №11 65 символов; №12 2 символа.






