Случайная величина (применительно к количественному анализу) — измеряемый аналитический сигнал (масса, объем, оптическая плотность и др.) или результат анализа.
Варианта — отдельное значение случайной величины, т. е. отдельное значение измерения аналитического сигнала или определяемого содержания.
Генеральная совокупность — идеализированная совокупность результатов бесконечно большого числа измерений (вариант) случайных величин.
Относительная вероятность результатов в генеральной совокупности при выполнении химико-аналитических определений в большинстве случаев описывается функцией Гаусса (распределением Гаусса).
Однако на практике невозможно (да и не нужно) проводить бесконечно большое число аналитических определений, поэтому используют не генеральную совокупность, а выборочную совокупность — выборку.
Выборка (выборочная совокупность) — совокупность ограниченного числа статистически эквивалентных вариант, рассматриваемая как случайная выборка из генеральной совокупности. Другими словами, выборочная совокупность — это совокупность результатов измерений аналитических сигналов или определяемых содержаний, рассматриваемая как случайная выборка из генеральной совокупности, полученной в указанных условиях.
Объем выборки — число вариант п, составляющих выборку. При статистической обработке результатов количественного анализа используют выборку, описываемую распределением Стьюдента.
Распределением Стьюдента предпочтительно пользоваться при объеме выборки п < 20.
Правильностью измерений называют качество измерений, отражающее близость к нулю систематических погрешностей.
Сходимостью измерений называют качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.
Более широкий смысл вкладывается в понятие «воспроизводимость».
Воспроизводимостью измерений называют качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (в разное время, разными методами и т. д.).
Точностью измерений называют качество измерений, отражающее близость их результатов к истинному значению измеряемой величины.
Высокая точность измерений соответствует малым погрешностям всех видов как систематическим, так и случайным. Количественно точность может быть выражена обратной величиной модуля относительной погрешности. Если, например, относительная погрешность измерения характеризуется значением 0,01%, то точность будет равна 1/10-4 = 104.
Результат анализа, приближающийся к истинному содержанию компонента настолько, что может быть использован вместо него, следует называть действительным содержанием.
Статистическая обработка и представление результатов количественного анализа
Расчет метрологических параметров. На практике в количественном анализе обычно проводят не бесконечно большое число определений, а п = 5— б независимых определений, т. е. имеют выборку (выборочную совокупность) объемом 5—6 вариант. В оптимальном случае рекомендуется проводить 5 параллельных определений (объем выборки п = 5).
При наличии выборки рассчитывают следующие метрологические параметры в соответствии с распределением Стьюдента.
Среднее, т. е. среднее значение определяемой величины, согласно (1.1),
| ` x = | å х i |
| n |
Среднее из конечной выборки отличается от действительного значения а (которое обычно не известно) и зависит от объема выборки п:
lim ` x ® a
при n ® ¥
Отклонение di:
di = xi ‑ ` x
— случайное отклонение i- ой варианты от среднего.
Дисперсия V (иногда ее обозначают как s 2) показывает рассеяние вариант относительно среднего и характеризует воспроизводимость анализа. Рассчитывается по формуле:
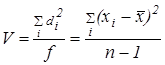
где f = n - 1 — так называемое число степеней свободы.
Если известно действительное значение определяемой величины а (или истинное значение определяемой величины m), например при работе со стандартным образцом, то среднее х принимают равным а (или m); тогда число степеней свободы f = n.
Дисперсия среднего V ` x, равна
V ` x = V / n
Стандартное отклонение (или среднее квадратичное отклонение) s — характеристика рассеяния вариант относительно среднего. Она рассчитывается как корень квадратный из дисперсии V, взятый со знаком плюс:
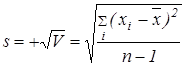
Очевидно, V = s2. Стандартное отклонение s, как и дисперсия V, характеризует воспроизводимость количественного анализа.
Стандартное отклонение среднего s ` x, определяется как

(«старое» название — средняя квадратичная ошибка среднего арифметического).
Доверительный интервал (доверительный интервал среднего) — интервал, в котором с заданной доверительной вероятностью Р находится действительное значение определяемой величины (генеральное среднее):
` x ± D` x
гдеD` x — полуширина доверительного интервала.
Доверительная вероятность Р — вероятность нахождения действительного значения определяемой величины а в пределах доверительного интервала. Изменяется от 0 до 1 или (что то же самое) от 0% до 100%. В фармацевтическом анализе при контроле качества лекарственных препаратов доверительную вероятность  чаще всего принимают равной Р == 0,95 = 95% и обозначают как Р0,95. При оценке правильности методик или методов анализа доверительную вероятность обычно считают равной Р = 0,99 = 99%.
чаще всего принимают равной Р == 0,95 = 95% и обозначают как Р0,95. При оценке правильности методик или методов анализа доверительную вероятность обычно считают равной Р = 0,99 = 99%.
Полуширину доверительного интервала их находят по формуле:
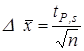
где tP,s — коэффициент нормированных отклонений (коэффициент Стьюдента, функция Стьюдента, критерий Стьюдента), который зависит от доверительной вероятности Р и числа степеней свободы f = п ‑ 1, т.е. от числа п проведенных определений.
Численные значения tP,s рассчитаны для различных возможных величин Р и n и табулированы в справочниках.
В табл. 1.1 приведены численные значения коэффициента Стьюдента, рассчитанные при разных величинах п и Р.
Чем больше п, тем меньше tP,s. Однако при п > 5 уменьшение tP,s ужесравнительно невелико, поэтому на практике обычно считают достаточным проведение пяти параллельных определений (п = 5).
Относительная (процентная) ошибка среднего результата `e:
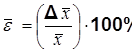
Исключение грубых промахов. Некоторые из результатов единичных определений (вариант), входящих в выборочную совокупность, могут заметно отличаться от величин остальных вариант и вызывать сомнения в их достоверности. Для того чтобы статистическая обработка результатов количественного анализа была достоверной, выборка должна быть однородной, т. е. она не должна быть отягощена сомнительными вариантами — так называемыми грубыми промахами. Эти грубые промахи необходимо исключить из общего объема выборки, после чего можно проводить окончательное вычисление статистических характеристик.
Если объем выборки невелик 5 < п < 10, то выявление сомнительных результатов анализа — исключение грубых промахов — чаще всего проводят с помощью так называемого Q-критерия. Для этого варианты xi вначале располагают в порядке возрастания их численного значения от х1 до хn, где п — объем выборки, т. е. представляют в виде упорядоченной выборки. Затем для крайних вариант — минимальной х 1 и максимальной хn — вычисляют величину Q пр формулам:
| Q 1 = | х 2 ‑ x2 | Q 1 = | х n ‑ xn -1 | |
| R | R |
где х 2 и xп‑ 1 — значения вариант, ближайших по величине к крайним вариантам, а
R = x n ‑ x 1
— размах варьирования, т. е. разность между максимальным х n и минимальным x 1 значениями вариант (между крайними вариантами), составляющих выборку.
Рассчитанные значения Q 1 и Q n сравнивают с табличными при заданных пи доверительной вероятности Р. Если рассчитанные значения Q1 или Qn (или оба) оказываются больше табличных
Q 1 > Q табл. Q 1 > Q табл.
то варианты х 1 или х n (или обе) считаются грубыми промахами и исключаются из выборки.
Для полученной выборки меньшего объема проводят аналогичные расчеты до тех пор, пока не будут исключены все грубые промахи, так что окончательная выборка окажется однородной и не будет отягощена грубыми промахами.
В табл. 1.2 приведены численные величины контрольного критерия Q для Р = 0,90—0,99 и n = 3—10.
Таблица 1.2. Численные значения Q -критерия при доверительной вероятности Р и объеме выборки n
 n
P n
P
| ||||||||
| 0,90 0,95 0,99 | 0,94 0,98 0,99 | 0,76 0,8,5 0,93 | 0,64 0,73 0,82 | 0,56 0,64 0,74 | 0,51 0,59 0,68 | 0,47 0,54 0,63 | 0,44 0,51 0,60 | 0,41 0,48 0,57 |
При проведении Q-mecma доверительную вероятность чаще всего принимают равной Р = 0,90 = 90%.
Если из двух крайних вариант х 1 и хn только одна вызывает сомнение. то Q -тест можно проводить лишь в отношении этой сомнительной варианты.
Пример статистической обработки и представления результатов количественного анализа.
Пусть содержание определяемого компонента в анализируемом образце, найденное в пяти параллельных единичных определениях (п = 5), оказалось равным, %: 3,01; 3,04; 3,08; 3,16 и 3,31. Известно, что систематическая ошибка отсутствует.
Требуется провести статистическую обработку результатов количественного анализа (оценить их воспроизводимость) при доверительной вероятности, равной Р = 0,95.
Решение. 1) Проведем оценку грубых промахов с использованием Q- критерия. Сомнительным значением может быть величина 3,31. Согласно формулам (1.10), имеем:
Q рассч = (3,31 ‑ 3,1б)/(3,31 ‑ 3,01) = 0,50.
Табличное значение Qтабл. при n = 5 и Р = 0,90 равно (табл. 1.2) Qтабл. = 0,64. Поскольку Qрассч. = 0,50 < Q табл. = 64, то значение варианты 3,31 не является грубым промахом. Выборка однородна.
2) Рассчитаем среднее значение ` х, отклонения di и сумму квадратов отклонений å d i2:
` x =(3,01 + 3,04 + 3,08 + 3,16 + 3,31)/5=3,12;
å d i2 = 0,0121 + 0,0064 + 0,0016 + 0,0016 + 0,0361 = 0,0578.
i Таблиц* отклонений
| xi | di = хi -` х | di2 |
| 3,01 3,04 3,08 3,16 3,31 | 3,01 ‑ 3,12 = ‑ 0,11 3,04 ‑ 3,12 = ‑ 0,08 3,08 ‑ 3,12 = ‑ 0,04 3,16 ‑ 3,12 = 0,04 3,31 ‑ 3,12 = 0,19 | 0,0121 0,0064 0,0016 0,0016 0,0361 |
3) Определяем стандартное отклонение по формуле (1.6):
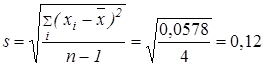
4) Определяем полуширину доверительного интервала среднего D` х по формуле (1.8) при п= 5 и Р= 0,95:
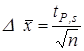
Коэффициент Стьюдента заимствуем из табл. 1.1:
tP,s = t0,95; 4 = 2,78
Тогда D`х = 2,78•0,12/50,5 = 0,15.
Доверительный интервал среднего:` х ± D` х = 3,12 ± 0,15.
5) Рассчитываем относительную ошибку среднего `e по формуле (1.9):
`e = (D` х /` х) × 100% = (0,15/3,12) × 100% = 4,8%
`e =(&x/x)• 100% = (0,15/3,12)-100% = 4,8%.
^
6) Составляем итоговую таблицу, представляющую результаты анализа.
Итоговая таблица
| x i | 3,01; 3,04; 3,08; 3,16; 3,31 |
| n | |
| `х | 3,12 |
| s | 0,12 |
| D`х | 0,15(P = 0,95) |
| `х ± D`х | 3,12 ± 0,15 |
| `e | 4,8% |
На этапе составления итоговой таблицы завершается представление результатов статистической обработки данных количественного анализа.
Нормальное распределение
Анализ экспериментальных данных показывает, что большие по значению погрешности наблюдаются реже, чем малые. Отмечается также, что при увеличении числа наблюдений одинаковые погрешности разного знака встречаются одинаково часто. Эти и некоторые другие свойства случайных погрешностей описываются нормальным распределением или уравнением Гаусса:
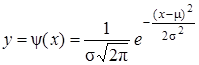 2.14
2.14
где y(х) — плотность вероятности; m — значение случайной величины; ц — генеральное среднее (математическое ожидание); s2 — дисперсия.
Равные по площади кривые нормального распределения приведены на рис. 2.1.
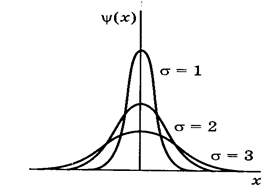
Рис. 2.1. Кривые нормального распределения при различной средней квадратичной погрешности
Как видно, чем больше стандартное отклонение (дисперсия), тем более пологой становится кривая.
Величины m и s называют параметрами распределения. Уравнение (2.14) описывает плотность вероятности. Коэффициент 1/sÖ2p— выбран так, чтобы вероятность попадания случайной величины х в интервал ‑¥ < х < ¥ была равна единице:
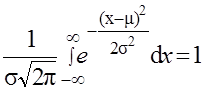 2.15
2.15
При любых значениях m и s площадь, ограниченная кривой (2.14) и осью абсцисс, равна единице. Очевидно, если через х 1 и х 2 провести ординаты, то случайная величина х попадает в интервал х 1 < х < х 2 с вероятностью
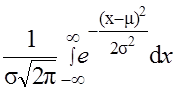
Расчеты показывают, что интеграл (2.15) в пределах от m — s до m + s составляет 68,3% общей площади, в пределах m ± 2s уже 95% ее, а при m ± 3s за интеграл равен практически всей площади, ограниченной кривой распределения и осью абсцисс (99,7%). Интеграл (2.15), равный на рис. 2.2 заштрихованной площади, показывает вероятность Р появления результата x i в указанной области значений х ± k s (от х ‑ k s до х + k s). Эту величину вероятности называют доверительной вероятностью или статистической надежностью, интервал от m ‑ k s до m + k s — доверительным интервалом, а границы интервала — доверительными границами. Таким образом, можно сказать, что доверительная вероятность получения результата в пределах от m ‑ s до m + s составляет 68,3%, т. е. в этих пределах лежит 2/3 всех результатов. Внутри пределов ± 2s будет находиться 95% всех значений, а диапазон ± 3s в охватывает 99,7%, т. е. практически все значения. Вероятность получения результата анализа, который будет находиться вне пределов интегрирования, равна a:
a = 1 ‑ Р.
Эту величину называют уровнем значимости. Классическая теория погрешностей, основанная на нормальном распределении, нашла широкое применение в астрономии, геодезии и других областях, где выполняется большое число измерений одной величины. Однако при обработке данных по анализу вещества она оказалась недостаточно эффективной, так как обычно приводила к заниженным, слишком оптимистичным значениям погрешности. Действительно, в соответствии с законом нормального распределения вероятность появления малых погрешностей значительно больше, чем вероятность появления больших, поэтому при небольшом числе наблюдений (параллельных проб) большие погрешности обычно не появляются, что и приводит к занижению погрешности, если небольшое число результатов обрабатывать в соответствии с нормальным распределением. Более корректная величина погрешности получается при использовании статистики малых выборок, развивающейся с начала XX в. (t -распределение, так называемое распределение Стьюдента и др.).-
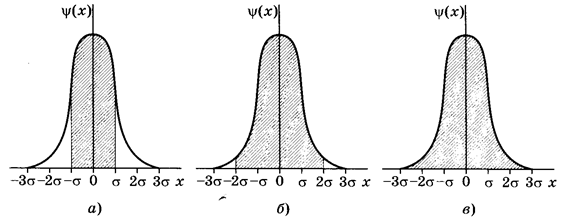
Рис. 2.2. Интегрирование уравнения Гаусса и пределах: а ‑ m ± s (68,3%); б — m ± 2s (95,0%); в — m ± 3s(99,7%,)
При расчетах окончательный результат обычно округляют. Округление следует проводить с соблюдением определенных правил, так как излишнее округление может ухудшить результаты анализа, а вычисления с неоправданно большим числом десятичных знаков без округления требуют больших, но напрасных затрат труда, поскольку не улучшают реальной точности результата.
При округлении обычно придерживаются следующих правил. Если за последней округляемой стоит цифра меньше 5, округляемую цифру оставляют без изменения (округление с уменьшением), а если больше 5, округляемую цифру увеличивают на единицу (округление с увеличением), например 4,7252 округляют до 4,725, но 4,7257 округляют до 4,726. Несколько сложнее правила округления, когда за последней округляемой цифрой стоит 5. Если за этой цифрой 5 нет более никаких цифр, то округляют до четной цифры, например, 4,7255 — 4,726, но 4,7245 - 4,724. Если за цифрой 5 имеется еще какая-либо отличная от нуля цифра, то округляют с увеличением, однако если 5 получено уже в результате округления, то округляют с уменьшением, т. е. 5 просто отбрасывают. Например, 4,72551 — 4,726, но 4,72548 - 4,7255 — 4,725.






