Цель работы
Изучение свободных затухающих колебаний, их графиков и характеристик. Определение времени релаксации, коэффициента затухания и логарифмического декремента затухания по экспериментальному графику изменения затухающих колебаний.
Теория работы
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени.
Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.
Одной из основных характеристик колебания является его амплитуда ¾ наибольшее отклонение колеблющегося тела от положения равновесия.
Незатухающими называются колебания, амплитуда которых с течением времени не изменяется. Затухающими называют колебания, амплитуда которых с течением времени убывает.
Свободное механическое колебание реального тела всегда затухающее. Причиной затухания являются неуничтожимые силы трения и другие потери энергии.
Уравнение свободного затухающего колебания (зависимость координаты от времени) можно получить, решив уравнение движения для колеблющегося тела. Таким уравнением является второй закон Ньютона. Рассмотрим тело, совершающее прямолинейные колебания в среде.
На тело действует сила упругости F упр и сила трения (сопротивление среды) F тр. По закону Гука:
F упр = - k × x
Знак минус учитывает то, что сила упругости всегда направлена к положению равновесия, т. е. выполняет роль возвращающей силы, являющейся причиной возникновения колебаний. Будем считать, что сила трения пропорциональна скорости движения тела:
v = dx /dt,
то есть
F тр = - b× (dx /dt).
Знак минус учитывает, что сила трения всегда направлена против направления движения. Сумма этих сил по второму закону Ньютона равна произведению массы тела на ускорение а = d2x /dt2:
F упр + F тр = m× a.
Учитывая выражение для сил и знаки, получим:
m  + b
+ b  + kx = 0 (1)
+ kx = 0 (1)
Разделим обе части на m и введя обозначения
 = w02,
= w02,
 = b,
= b,
получим дифференциальное уравнение второго порядка для свободного затухающего колебания:
 + 2b
+ 2b  + w02x = 0. (2)
+ w02x = 0. (2)
Явную зависимость x =x(t) координаты от времени называют уравнением затухающего колебания и получают в результате решения (2):
x = A0× e- bt × cos(wt + j); (3)
график затухающего колебания имеет вид (рис. 1).

Рис. 1
где А0 – начальная амплитуда (при t = 0); e =2,718 – основание натурального логарифма; b – коэффициент затухания, который измеряется в с-1; w – циклическая частота колебаний, которая измеряется в рад/с; t – время колебаний; j – начальная фаза колебаний.
Амплитуда затухающих колебаний убывает со временем по закону:
А = А0е-bt. (4)
Циклическая частота затухающего колебания:
 , (5)
, (5)
где w0 – циклическая частота колебаний при отсутствии трения, т. е. незатухающего колебания. При увеличении потерь (возрастании b) циклическая частота затухающих колебаний w уменьшается, а при условии:
w0 £ b (6)
– колебания невозможны.
Начальная фаза j определяет начальное смещение x0 при t=0:
x0=A0×cos(j) (7)
На рис. 1 дан график затухающего колебания, проходящего по закону косинуса при j = 0. Время t, в течение которого амплитуда уменьшается в e раз, называют временем релаксации:
A (t)/A (t+t)=e (8)
т. к.  , то ebt=e.
, то ebt=e.
Поэтому справедливо соотношение:
bt = 1 (9)
Частотой колебаний n называют количество колебаний за 1 с, а периодом T – время одного колебания. Частота и период связаны соотношением:
T =  . (10)
. (10)
За одно колебание фаза изменяется на 2p, а за 1 с – на 2pn или на w, т. е.:
w = 2pn =  . (11)
. (11)
Декрементом затухающего колебания называют величину D, показывающую во сколько раз амплитуда колебаний в данный момент A(t) больше той, которая будет через один период, т. е.:
 (12)
(12)
Логарифмическим декрементом d называют натуральный логарифм декремента, т. е.:
d = ln D. (13)
Справедливо соотношение:
d = bT; b =  (14)
(14)
Действительно,

Используя (11) и (14), уравнение затухающего колебания (3) можно записать в виде:
 (15)
(15)
Описание установки
Установка (рис. 2) представляет собой физический маятник в виде стержня с закрепленным на его нижнем конце диском, предназначенным для увеличения затухания за счет сопротивления воздуха. На маятник могут крепиться дополнительные грузы для изменения времени релаксации. Смещение маятника и амплитуда отсчитывается по шкале. Время измеряется по механическому или электрическому секундомеру.
Порядок выполнения работы и обработка результатов
1. Отклонить маятник на 40-50 делений (это и есть начальная амплитуда А0).
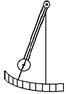
Рис. 2
2. Отпустить маятник, одновременно включив секундомер. Измерить время t двадцати колебаний и вычислить период: T = t/n., где n=20.
3. Вычислить циклическую частоту w.
4. Вновь отклонить маятник до выбранного значения А0 (40-50делений) и, опустив его, определить амплитуду пятого, десятого, пятнадцатого, двадцатого, двадцать пятого, тридцатого колебаний. Снять не менее шести значений.
5. Зная период T, рассчитать время данных колебаний, как tn = T× n, где n – число колебаний.
6. Построить график зависимости амплитуды от времени А= А(t).
7. По графику найти время релаксации t (см. рис. 1).
8. Рассчитать коэффициент затухания, используя соотношение (9).
9. Рассчитать логарифмический декремент, используя (14).
10. Результаты измерений и расчетов занести в таблицу, составленную по собственному усмотрению.
11. Записать уравнения колебаний с использованием b, w, d, T, v. Указать значение начальной фазы j в эксперименте.
12. Оценить погрешность эксперимента
e% =  .
.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Определение свободных незатухающих и затухающих колебаний.
2. Вывод дифференциального уравнения затухающих колебаний.
3. Уравнение затухающих колебаний.
4. Характеристики затухающего колебания: А, А0, w, j, Т, v, b, d, t, их смысл, единицы измерения и взаимосвязь.
5. Вывод соотношений bt = 1 и dT = 1.
6. Графики затухающего колебания и амплитуды затухающего колебания.
7. Определение t из графика амплитуды.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Детлаф А. А., Яворский Б. М., Милковская Л. Б. Курс физики. – М.: Высш. шк, 1973. – С 8.1, 8.2, 8.5.
2. Геворкян Р. Г., Шепель В. В. Курс общей физики: В 2 т. Т.1. – М.: Высш. шк., 1972г. – С.24.
3. Трофимова Т. И., Курс физики. – М.: Высш. шк., 1998г.






