По результатам испытаний для нескольких образцов при различных нормальных напряжениях строят график зависимости касательных и нормальных напряжений.
Для этого через опытные точки проводят прямую линию, занимающее среднее положение между всеми точками
Опытами установлено, что график зависимости предельного сопротивления грунтов сдвигу от нормального напряжения для идеально сыпучих грунтов в пределах изменения напряжений, представляющих интерес для строительства (до 0,3-0,6 МПа), с достаточной степенью точности может быть принят за прямую линию, выходящую из начала координат и наклоненную под углом к оси нормальных напряжений (рис. 3).

Рис 3. График зависимости сопротивления сдвигу от нормального напряжения для песков
Согласно графику зависимость между касательным и нормальным напряжениями выражается уравнением


где f = tgj - коэффициент внутреннего трения.
Угол j - угол внутреннего трения является прочностной характеристикой для песков. Угол j может быть получен по графику зависимости t = f(s)

|
Соотношение является основной прочностной зависимостью для сыпучих грунтов, носит название закона Кулона и формулируется следующим образом; предельной сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному напряжению
Рис 4. График зависимости сопротивления сдвигу от нормального напряжения для глинистых грунтов
Для глинистых грунтов зависимость между касательными и нормальными напряжениями имеет более сложный характер в связи с тем, что сопротивление сдвигу обусловливается не только силами трения, но и связностью грунта (пластичными водно-коллоидными и частично жесткими – цементационно-кристаллизационными связями). Однако, как и для сыпучих грунтов, зависимость сопротивления сдвигу от нормальных напряжений представляется прямой линией (рис. 4).
Эта зависимость согласно графику (рис. 4) описывается уравнением
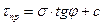
Приняв f = tga, получим

Коэффициент f = tga по аналогии с сыпучими грунтами носит название коэффициента внутреннего трения. Параметр с, не зависящий в явном виде от величины внешнего давления, называется удельным сцеплением глинистых грунтов и характеризует его связность.
Прочностные характеристики грунта – угол внутреннего трения и удельное сцепление с, МПа, получают по графику зависимости (рис. 4). При этом величину с определяют как отрезок, отсекаемый прямой на оси ординат, а тангенс угла наклона этой прямой к оси абсцисс есть тангенс угла внутреннего трения.
Уравнение выражает закон Кулона для глинистых грунтов, который формулируется следующим образом: предельное сопротивление связных грунтов сдвигу при завершенной их консолидации есть функция первой степени от нормального напряжения
Если прямую АВ (рис. 4) продлить до пересечения с осью абсцисс, то она отсечет отрезок 00', называемый давлением связности ре, суммарно заменяющее действие сил сцепления. Из треугольника ОО'А величины удельного сцепления с и связности рс будут равны:


Выражения часто используют в задачах теории предельного равновесия грунтом для вычисления величин, заменяющих силы сцепления связных грунтов.
| Касательное напряжение | 0,6 | 1,23 | 1,78 |
| Нормальное напряжение | 0,1 | 0,2 | 0,3 |
 Þ j = 71о
Þ j = 71о
Угол естественного откоса
Под углом естественного откоса понимают угол наклона образующей конуса или угол наклона, образуемый поверхностью неукрепленного сыпучего (рыхлого) грунта (например, песка), свободно насыпаемого на горизонтальную плоскость, с этой плоскостью. Существует зависимость между углом естественного откоса и коэффициентом сыпучести. Чем больше коэффициент сыпучести, тем меньше угол естественного откоса. Величина угла естественного откоса зависит от формы и крупности частиц грунта и его влажности. Знание угла естественного откоса используется при разработке и добыче строительных материалов и других полезных ископаемых, при складировании сыпучих материалов и т.д.
Угол естественного откоса песков в сухом состоянии равен углу внутреннего трения.






