Лабораторная работа № 6
Интегральной функцией распределения называют функцию F(x), определяющую для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее х, т.е.
.
Интегральная функция обладает следующими свойствами:
1. Значения интегральной функции принадлежат отрезку [0; 1]
.
2. Интегральная функция является неубывающей функцией, т.е. 
.
3. Вероятность того, что случайная величина Х примет значения, заключенные в интервале (a; b), равна приращению интегральной функции на этом интервале 
.
4. Вероятность того, что случайная величина Х примет одно определенное значения, например х1, равна нулю
.
5. Если все возможные значения случайной величины Х принадлежат интервалу (a; b), то 
.
6. Справедливы следующие предельные соотношения:
.
Дифференциальной функцией распределения вероятностей (плотности вероятностей) называют первую производную от интегральной функции:
.
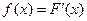Вероятность того, что непрерывная случайная величина Х принимает значение, принадлежащие интервалу (a; b) определяется равенством
.
Зная дифференциальную функцию, можно найти интегральную функцию по формуле
.
Дифференциальная функция обладает следующими свойствами:
1. Дифференциальная функция неотрицательна, т.е.
.
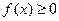2. Несобственный интеграл от дифференциальной функции в пределах от -∞ до +∞ равен единице:
.
В частности, если все возможные значения случайной величины принадлежат интервалу (a; b), то
.
Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством
,
где f(x) – дифференциальная функция. Предполагается, что интеграл сходится абсолютно.
В частности, если все возможные значения случайной величины принадлежат интервалу (a; b), то
.
Модой М0(Х) непрерывной случайной величины называют то её возможное значение, которому соответствует максимум дифференциальной функции.
Медианой Ме(Х) непрерывной случайной величины называют то её возможное значение, которое определяется равенством
.
Геометрически медиану можно истолковать как точку, в которой ордината f(x) делит пополам площадь, ограниченную кривой распределения.
Дисперсия непрерывной случайной величины Х определяется равенством
,
или равносильным равенством
.
Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной величины:
.
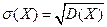Начальный теоретический момент порядка k непрерывной случайной величины Х определятся равенством
.
Центральный теоретический момент порядка k непрерывной случайной величины Х определятся равенством
.
Очевидно, что если k = 1, то ν1 = М(Х), μ1 = 0, если k = 2, то μ2 = D(X). Центральные моменты выражаются через начальные моменты по формулам:
.
Равномерным называют распределение вероятность непрерывной случайной величины Х, если на интервале (a; b), которому принадлежат все возможные значения Х, дифференциальная функция постоянна и равна
,
и f(x) = 0 вне этого интервала.
Нормальным называют распределение вероятностей непрерывной случайной величины Х, дифференциальная функция которой имеет вид
,
где μ – математическое ожидание, σ – среднее квадратическое отклонение случайной величины Х.
Вероятность того, что Х примет значение, принадлежащее интервалу (α; β),
,
где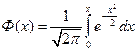 
- функция Лапласа.
Вероятность того, что абсолютная величина отклонения меньше положительного числа δ,
.
В частности, при μ = 0 справедливо равенство
.
Мода и медиана нормального распределения соответственно равны:
где μ = M(X).
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается дифференциальной функцией
где λ – постоянная положительная величина.
Интегральная функция показательного распределения
Вероятность попадания в интервал (a; b) непрерывной случайной величины Х, распределенной по показательному закону,
.
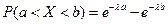Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределение соответственно равны:
Пример Построить графики плотности вероятностей и интегральной функции распределения случайной величины Х, имеющей равномерное распределение на отрезке [0; 1]. Найти математическое ожидание и дисперсию случайной величины Х и вероятность попадания случайной величины Х в интервал (0.5; 1.5).
Решение. 
Варианты заданий к лабораторной работе №6.
Построить графики плотности вероятностей и интегральной функции распределения случайной величины Х, имеющей нормальное, с параметрами μ, σ. и показательное распределение с параметром λ. Найти математическое ожидание и дисперсию случайной величины Х и вероятность попадания случайной величины Х в интервал (α; β).
| № | μ | σ | λ | α | β |
| 1.5 | 0.8 | 0.5 | |||
| 0.6 | 0.9 | 0.8 | |||
| 0.5 | 1.1 | 0.7 | 0.6 | 1.2 | |
| 0.5 | 0.8 | 0.6 | 0.3 | 0.4 | |
| 0.4 | 0.5 | 2.1 | |||
| 0.3 | 1.1 | 0.4 | 1.1 | ||
| 0.2 | 1.2 | 0.3 | 1.5 | 2.8 | |
| 0.1 | 1.3 | 0.2 | 1.6 | ||
| 0.1 | 1.3 | 2.3 | |||
| -0.2 | 1.1 | 0.3 | -0.1 | 0.4 | |
| -0.3 | 1.2 | 0.4 | -0.2 | 0.5 | |
| -0.4 | 1.3 | 0.5 | -0.1 | 0.6 | |
| -0.5 | 1.4 | 0.6 | 0.7 | ||
| -0.6 | 1.3 | 0.7 | 0.1 | 0.4 | |
| -0.7 | 1.5 | 0.8 | 0.3 | 0.9 | |
| -0.8 | 1.6 | 0.9 | 0.6 | 1.1 | |
| -0.9 | 1.7 | 0.7 | 1.3 | ||
| -1 | 1.8 | 1.1 | 0.4 | 0.9 | |
| -1.1 | 1.9 | 1.2 | 0.5 | 1.2 | |
| 1.8 | 0.4 | 2.5 | |||
| 0.9 | 1.7 | 0.5 | 1.8 | ||
| 0.8 | 1.6 | 0.6 | 1.5 | 2.6 | |
| 0.7 | 1.5 | 0.7 | 1.1 | 2.3 | |
| 0.6 | 1.4 | 0.8 | 1.3 | 2.7 | |
| 0.5 | 1.3 | 0.9 | 0.8 | 1.4 | |
| 0.4 | 1.2 | 0.6 | 1.3 | ||
| 0.3 | 1.1 | 1.1 | 0.5 | 0.9 | |
| 0.2 | 1.2 | 0.4 | 0.8 | ||
| 0.1 | 0.9 | 1.3 | 0.3 | 0.7 |
