Глава 1
МАТРИЦЫ.
1.Матрицы. Матрицей А называется прямоугольная таблица, состоящая из m строк и n столбцов:
Числа a ij, i= 1, m, j=1, n, называются элементами матрицы. Пара чисел (m,n) определяет размер (тип) матрицы А. Для удобства часто используется краткая запись матрицы:
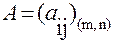
Матрицы размера (m,n) образуют множество, которое будем обозначать через М(m,n). В случае, когда m=n,матрица называется квадратной. Число m=n называется порядком квадратной матрицы.
Суммой A+B матриц A, B ϵ 
называется матрица C ϵ ,
элементы которой равны сумме соответствующих элементов матрицы А и В:
Cij = Aij +Bij, i = 1, m, j =1, n.
Произведением 
λА матрицы A ϵ на число λ называется матрица
B ϵ , элементы которой равны проиведениям соответствующих элементов матрицы А на число λ: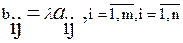 
Произведением АВ матрицы A ϵ на число λ называется матрица
B ϵ , элементы которой равны произведениям соответствующих элементов матрицы А на число λ:
Произведением АВ матрицы А ϵ М (m,n) на матрицу B ϵ M (n,k)называется матрица C ϵ , элементы Cij которой равны сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В:
Cij=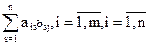 
Произведение Х=А(ВС) удобно находить по схеме Фалька:
| B | C | |
| A | AB | X |
Если А – невырожденная квадратная матрица (det A≠0),то существует и притом единственная матрица А· 
= А= Е, где Е – единичная матрица
Чтобы найти матрицу , обратную к невырожденной квадратной матрице А, необходимо:
Вычислить определитель 
= det А матрицы А;
Найти алгебраические дополнения А ij каждого элемента a ij определителя ;
Составить из чисел Аij матрицу А, присоединенную к матрице А;
Транспонируя матрицу А, составить А*; умножить матрицу А* на число 
.В результате получим матрицу 
= А*, обратную к матрице А.
2.Системы линейных уравнений. Пусть задана совместная система n линейных уравнений с n неизвестными:
Введем обозначения
, 
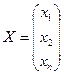. В = 
,
Тогда в систему (1) можно записать в матричной форме АХ=В.
1.Правило Крамера. Если в системе (1) = det А 
0,то
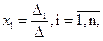
Где t – определитель, получаемый из определителя с заменой i-го столбца на столбец свободных членов.
2.Метод обратной матрицы. Умножая обе части уравнения (2) слева на матрицу и учитывая, что А = Е, ЕХ = Х, получим искомое решение Х = В.
3.Метод Жордана – Гаусса. Записав расширенную матрицу системы (1), с помощью элементарных преобразований ее можно привести к треугольному виду
Полученная матрица является расширенной матрицей системы
Эквивалентной системе (1). Решение системы (1`) имеет
Оно является также решением исходной системы(1)
Исследование систем линейных уравнений на местность, а также решение однородных систем в данной главе мы не рассматриваем.
Задача 1.1. Два железобетонных завода выпускали изделия M,N,P высшей, первой и второй категории качества. Количество выпущенных каждым заводом изделий по каждой категории качества характеризуется следующей таблицей:
(идет таблица)
Каков общий выпуск изделий по указанным категориям качества?
Количество изделий, выпущенных первым заводом можно рассматривать как элементы матрицы В:
(таблица)
Складывая их, получим матрицу С, определяющую общее число изделий по указанным категориям качества:
(таб)
Задача 1.2. В соответствии с программой строительно-монтажных работ установлено, что будет сооружено:
а) в отрасли Х1 10 единиц объектов типа 1 и 15 единиц типа 2;
б) в отрасли Х2 20 единиц объектов типа 3;
в) в отрасли Х3 100 единиц объектов типа 5.
Определить расходы строительных материалов видов p и q в каждой отрасли,если нормы расхода материалов (в соответствующих единицах измерения) приведены в следующей таблице:
(таб)
Введем матрицы: М – матрица исходных данных по объектам строительства, А – матрица норм расхода материалов:
(таб)
Тогда матрица расхода материалов p и q имеет вид
(таб)
т.е. расход материала p в отраслях Х1, Х2 , Х3 соответственно составляет 170, 200,500 единиц,а материалов q соответственно 450,2000,5000 единиц.
Задача 1.3. При изготовлении строительных деталей четырех видов расход материалов, рабочей силы и электроэнергии задается таблицей(в условных единицах)
(таб)
Вычислить общую потребность материалов (у1),рабочей силы (у2) и электроэнергии (у3) для изготовления заданного колличества хi деталей каждого вида:
х1=10, х2 =2, х3= 8, х4 =4
Общая потребность в материалах,рабочей силе и электроэнергии для изготовления количества хi деталей каждого вида определяется уравнением
Y = AX,
Где Y= (таб) - матрица общей потребности в ресурсах;
