Замена переменной и интегрирование по частям в определенном интеграле
Теорема. Пусть дан интеграл 
, где 
непрерывна на 
. Введем новую переменную 
, связанную с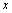 
равенством 
. Если
1) 
2) 
и 
непрерывны на 
3) при изменении z от α до β значения не выходят за пределы отрезка 
то 
(5)
Доказательство. Пусть 
–первообразная для функции то есть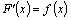 
.. Тогда по формуле Ньютона–Лейбница
(I)
Покажем, что функция 
является первообразной для функции 
: 
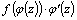=[по правилу дифференцирования сложной функции] =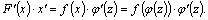 
Тогда по формуле Ньютона–Лейбница
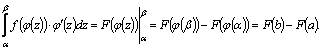(II)
Сравнивая равенства (I) и (II), убеждаемся в справедливости формулы (5).
Пример.
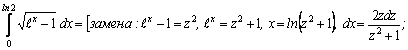
при x=0 
при x=ln2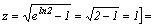 
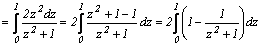
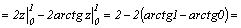
Интегрирование по частям в определенном интеграле
Формула интегрирования по частям в определенном интеграле выводится так же, как и для неопределенного интеграла, и имеет вид
Пример.
Приложения определенного интеграла
Приведем без вывода основные формулы и примеры геометрических приложений определенного интеграла.
1. Вычисление площади в декартовых координатах.
Площадь криволинейной трапеции, ограниченной кривой 
непрерывна), прямыми x=a, x=b и осью Ox (рис.6) равна
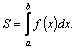(6)
Площадь фигуры, ограниченной кривой 
непрерывна), прямыми x=a, x=b и осью Ox (рис.7) равна
(7)
Площадь фигуры, ограниченной двумя непрерывными кривыми 
и 
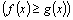и прямыми x=a и x=b 
(рис.8) равна
(8)
Площадь фигуры, ограниченной кривыми и 
и 
неотрицательны и непрерывны), пересекающимися в точке с абсциссой x=b, прямыми x=a, x=c и осью Ox (Рис.9), равна
(9)
В случае параметрического задания кривой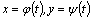 
площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и осью Ox (рис.6) равна
(10)
Где 
и 
определяются из уравнений 
на отрезке 
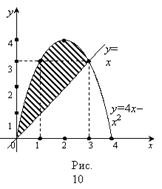
Пример1. Найти площадь, ограниченную линиями
и 
Решение. Одна из линий–парабола, другая–прямая (рис.10).
Найдем их точки пересечения 
Тогда по формуле (8)
Системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 
, которую назовём матрицей системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
1.Система может иметь единственное решение.
2.Система может иметь бесконечное множество решений. Например,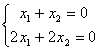 
. Решением этой системы является любая пара чисел, отличающихся знаком.
3.И третий случай, когда система вообще не имеет решения. Например, 
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
