Алгоритм решения способом сложения

Рациональные уравнения

Функция вида

P(x) = a₀xⁿ + a₁x^{n – 1}+ a₂x^{n – 2}+ … + a_{n – 1}x + a_n,

где n — натуральное, a₀, a₁,…, a_n — некоторые действительные числа, называется целой рациональной функцией.

Уравнение вида P(x) = 0, где P(x) — целая рациональная функция, называется целым рациональным уравнением.

Уравнение вида

P₁(x) / Q₁(x) + P₂(x) / Q₂(x) + … + P_m(x) / Q_m(x) = 0,

где P₁(x), P₂(x), …,P_m(x), Q₁(x), Q₂(x), …, Q_m(x) — целые рациональные функции, называется рациональным уравнением.

Решение рационального уравнения P (x) / Q (x) = 0, где P (x) и Q (x) — многочлены (Q (x) ¹ 0), сводится к решению уравнения P (x) = 0 и проверке того, что корни удовлетворяют условию Q (x) ¹ 0.

Пример 1. Решить уравнение

2x – 3 + 4(x – 1) = 5.

Решение. Последовательно раскроем скобки, приведём подобные члены и найдём x: 2x – 3 + 4x – 4 = 5, 2x + 4x = 5 + 4 + 3,

6x = 12, x = 2.

Ответ: 2.

Рациональные неравенства

Рациональное неравенство с одной переменной х — это неравенство вида 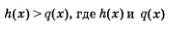— рациональные выражения, т.е. алгебраические выражения, составленные из чисел и переменной х с помощью операций сложения, вычитания, умножения, деления и возведения в натуральную степень.

Пример 1. Решить неравенство (х - 1) (х + 1) (х - 2) > 0.

Решение. Рассмотрим выражение f(х) = (х-1)(х + 1)(х-2).

Оно обращается в 0 в точках 1,-1,2; отметим эти точки на числовой прямой. Числовая прямая разбивается указанными точками на четыре промежутка (рис. 6), на каждом из которых выражение f (x) сохраняет постоянный знак. Чтобы в этом убедиться, проведем четыре рассуждения (для каждого из указанных промежутков в отдельности).

Возьмем любую точку х из промежутка (2, Эта точка расположена на числовой прямой правее точки -1, правее точки 1 и правее точки 2. Это значит, что х > -1, х >1, х > 2 (рис. 7). Но тогда x-1>0, х+1>0, х - 2 > 0, а значит, и f (х) > 0 (как произведение рациональное неравенство трех положительных чисел). Итак, на всем промежутке 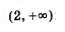выполняется неравенство f (x) > 0.

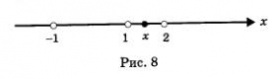
Возьмем любую точку х из интервала (1,2). Эта точка расположена на числовой прямой правее точки-1, правее точки 1, но левее точки 2. Значит, х > -1, х > 1, но х < 2 (рис. 8), а потому x + 1>0,x-1>0,x-2<0. Но тогда f(x) <0 (как произведение двух положительных и одного отрицательного числа). Итак, на промежутке (1,2) выполняется неравенство f (x) < 0.

Возьмем любую точку х из интервала (-1,1). Эта точка расположена на числовой прямой правее точки -1, левее точки 1 и левее точки 2. Значит, х >-1, но х< 1, х <2 (рис. 9), а потому х + 1 > 0, х -1 <0, х - 2 < 0. Но тогда f (x) > 0 (как произведение двух отрицательных и одного положительного числа). Итак, на промежутке (-1,1) выполняется неравенство f (x)> 0.

Возьмем, наконец, любую точку х из открытого луча (-оо, -1). Эта точка расположена на числовой прямой левее точки -1, левее точки 1 и левее точки 2. Это значит, что x<-1, х< 1, х<2 (рис. 10). Но тогда x - 1 < 0, x + 1 < 0, х - 2 < 0, а значит, и f (x) < 0 (как произведение трех отрицательных чисел). Итак, на всем промежутке (-оо, -1) выполняется неравенство f (x) < 0.

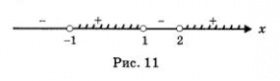
Подведем итоги. Знаки выражения f (x) в выделенных промежутках таковы, как показано на рис. 11. Нас интересуют те из них, на которых выполняется неравенство f (x) > 0. С помощью геометрической модели, представленной на рис. 11, устанавливаем, что неравенство f (x) > 0 выполняется на интервале (-1, 1) или на открытом луче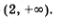
О т в е т: -1 < х < 1; х > 2.

2.Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени.

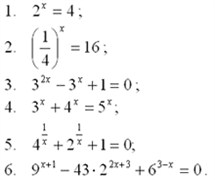Решение показательных уравнений часто сводится к решению уравнения а^х = а^b, где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:

Теорема. Если а > 0, а ≠ 1 и а^х1 = а^х2, то х₁ = х₂.

Обоснуем рассмотренное утверждение.

Предположим, что равенство х₁ = х₂ не выполняется, т.е. х₁ < х₂ или х₁ = х₂. Пусть, например, х₁ < х₂. Тогда если а > 1, то показательная функция у = а^х возрастает и поэтому должно выполняться неравенство а^х1 < а^х2; если 0 < а < 1, то функция убывает и должно выполняться неравенство а^х1 > а^х2. В обоих случаях мы получили противоречие условию а^х1 = а^х2.

Рассмотрим несколько задач.

Задача 1.

Решить уравнение 4 ∙ 2^х = 1.

Решение.

Запишем уравнение в виде 2²∙ 2^х = 2⁰ – 2^х+2 = 2⁰, откуда получаем х + 2 = 0, т.е. х = -2.

Ответ. х = -2.

Решение показательных неравенств часто сводится к решению неравенств а^х > а^b или а^х < а^b. Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции.

Рассмотрим некоторые задачи.

Задача 1.

Решить неравенство 3^х < 81.

Решение.

Запишем неравенство в виде 3^х < 3⁴. Так как 3 > 1, то функция у = 3^х является возрастающей.

Следовательно, при х < 4 выполняется неравенство 3^х < 3⁴, а при х ≥ 4 выполняется неравенство 3^х ≥ 3⁴.

Таким образом, при х < 4 неравенство 3^х < 3⁴ является верным, а при х ≥ 4 – неверным, т.е. неравенство
3^х < 81 выполняется тогда и только тогда, когда х < 4.

Ответ. х < 4.

Логарифмические уравнения

Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.

Простейшим логарифмическим уравнением является уравнение вида

log _a x = b.

(1)

Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = a^b.

Пример 1. Решить уравнения:

a) log₂ x = 3

Решение a) x = 2³ или x = 8;

Перечислим и основные свойства логарифмической функции f (x) = log _a x:

Область определения логарифмической функции есть множество положительных чисел.
Область значений логарифмической функции - множество действительных чисел.
При a > 1 логарифмическая функция строго возрастает (0 < x ₁ < x ₂ Þ log _a x ₁ < log _a x ₂), а при 0 < a < 1, - строго убывает (0 < x ₁ < x ₂ Þ log _ax ₁ > log _a x ₂).
log _a 1 = 0 и log _aa = 1 (a > 0, a ≠ 1).
Если a > 1, то логарифмическая функция отрицательна при x Î (0;1) и положительна при x Î (1;+¥), а если 0 < a < 1, то логарифмическая функция положительна при x Î (0;1) и отрицательна при x Î (1;+¥).
Если a > 1, то логарифмическая функция выпукла вверх, а если a Î (0;1) - выпукла вниз.

4. При изучении логарифмической функции мы рассматривали в основном неравенства вида
log_а х < b и log_а х ≥ b. Рассмотрим решение более сложных логарифмических неравенств. Обычным способом решения таких неравенств является переход от данного неравенства к более простому неравенству или системе неравенств, которая имеет то же самое множество решений.

Задача 1.

Решить неравенство lg (х + 1) ≤ 2 (1).

Решение.

1) Правая часть рассматриваемого неравенства смысл имеет при всех значенияхх, а левая часть – при х + 1 > 0, т.е. при х > -1.

2) Промежуток х > -1 называют областью определения неравенства (1). Логарифмическая функция с основанием 10 является возрастающей, следовательно, при условии х + 1 > 0 неравенство (1) выполняется, если х + 1 ≤ 100 (так как 2 = lg 100). Таким образом, неравенство (1) и система неравенств

{х > -1, (2)
{х + 1 ≤ 100,

равносильны, иными словами, множество решений неравенства (1) и системы неравенств (2) одно и то же.

3) Решая систему (2), находим -1 < х ≤ 99.

Ответ. -1 < х ≤ 99.

5.Метод подстановки

Алгоритм:

1) Выразить одну из переменных, из любого уравнения системы;

2) Подставить полученное выражение в другое уравнение;

3) Решить полученное уравнение с одной переменной;

4) Подставить найденное значение переменной в выражение для другой переменной и найти ее значение;

5) Записать ответ в виде пары чисел (х;у);

6) Сделать проверку.

Пример:

выражаем у из (1) уравнения: у=2х-9

подставляем во (2) уравнение: 5х+14х-63=44

решаем его: 19х=107; х=107/19

подставляем в выраженное у и получаем: у=43/19.

Ответ: (107/19; 43/19)

Алгоритм решения способом сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.

2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным

3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.

4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.

5. Сделать проверку решения.